Откуда ты вылез, из 18 века? В современном анализе не используется понятие бесконечно малой. Есть понятие величины, неограниченно приближающейся к чему-то, нулю, в твоем случае.
Этот еблан смешал анализ 1 курса и нестандартный анализ, который не каждый проф понимает, из того, что я понял. Такие вот сомнения возникают от плохого понимания предела. Анон, разбери понятие предела просто как конструкцию. БЕСКОНЕЧНО МАЛАЯ ФУНКЦИЯ -- ЭТО ПРОСТО УСЛОВНОСТЬ. Не нужно его понимать буквально, просто привыкни к определению.
Пиздец, школу закончите, лалки, "бесконечно большая и бесконечно малая в точке функция" (цитата из ОП-поста) - это строго определённые термины.
Давайте общаться по теме, что такое бесконечно малая или бесконечно большая функция в точке?
Читаем статью на mathprofi.ru:
lim{k->1}f(x)=0 - функция бесконечно мала в точке k, если существует такой предел.
Теперь первый пример пошёл (на картинках):
lim{x->0}(x)=0 - функция бесконечно мала в точке (0,0).
(x) здесь это f(x).
Короче, тут написано, что функция РАВНА нулю, когда x ещё только СТРЕМИТЬСЯ к нулю.
А во втором примере, функция уже равна нулю, когда x ещё стремится к 1 или 2.
Мы абсолютно точно знаем, что в первом примере, y=0 тогда и только тогда, когда x=0.
А во втором y=0 тогда и только тогда, когда x=1 и x=2.
Стремление не есть равно. Если x только стремится к точке, то и y тоже только стремится к точке, но тогда до точки никакой точки y=0 в реале и нет, ведь стремление это бесконечно, а когда мы берём x значение той точки, тогда y приобретает значение НОЛЬ и в этот момент x у нас никуда не стремится, а чётко равен нулю!
И опять же, в том же пределе написано, что f(x)=0, т.е. y=0. Тогда какая это "бесконечно малая", если там чёткий ноль?
Что это за идиотия?
Наверно, записываться это должно так (для первого примера):
lim{x->0}(x)->0 Это и есть бесконечно малое значение функции по модулю, но только нихрена не в точке, а на бесконечном промежутке до нуля.
x=0 => f(x)=0 А это уже максимально малое по модулю значение функции.
На самом деле...
-1<1
Бесконечно малая функция стремится к минус бесконечность и нет там никакой точки вообще.
Читаем статью на mathprofi.ru:
lim{k->1}f(x)=0 - функция бесконечно мала в точке k, если существует такой предел.
Теперь первый пример пошёл (на картинках):
lim{x->0}(x)=0 - функция бесконечно мала в точке (0,0).
(x) здесь это f(x).
Короче, тут написано, что функция РАВНА нулю, когда x ещё только СТРЕМИТЬСЯ к нулю.
А во втором примере, функция уже равна нулю, когда x ещё стремится к 1 или 2.
Мы абсолютно точно знаем, что в первом примере, y=0 тогда и только тогда, когда x=0.
А во втором y=0 тогда и только тогда, когда x=1 и x=2.
Стремление не есть равно. Если x только стремится к точке, то и y тоже только стремится к точке, но тогда до точки никакой точки y=0 в реале и нет, ведь стремление это бесконечно, а когда мы берём x значение той точки, тогда y приобретает значение НОЛЬ и в этот момент x у нас никуда не стремится, а чётко равен нулю!
И опять же, в том же пределе написано, что f(x)=0, т.е. y=0. Тогда какая это "бесконечно малая", если там чёткий ноль?
Что это за идиотия?
Наверно, записываться это должно так (для первого примера):
lim{x->0}(x)->0 Это и есть бесконечно малое значение функции по модулю, но только нихрена не в точке, а на бесконечном промежутке до нуля.
x=0 => f(x)=0 А это уже максимально малое по модулю значение функции.
На самом деле...
-1<1
Бесконечно малая функция стремится к минус бесконечность и нет там никакой точки вообще.
Я уже закончил, а ты хуйней какой-то занимаешься. По конспекту Письменного учился? Я только там видел упоминания этого говна.
А если убрать модуль функции.
lim{x->0}(x)->0 тут x стремиться к нулю с двух сторон и y анлогично стремится к нулю с двух сторон и мы получаем уже две псевдоточки.
Псевдоточки - потому что нет там никаких нужных нам точек (x,0), а есть только бесконечное стремление к ней, и во всех y не равен ноль.
Вторая часть системы:
x=0 => f(x)=0
Убираем модуль функции и опять получаем две псевдоточки для каждой точки (а всего 4).
я сейчас учусь и учусь по mathprofi.
В любом учебнике Анализа, от Зорича до Шварца, лучше бы не заканчивал, дебил.
Если ты сам идиот, так хоть других не агитируй становиться идиотами.
> lim{k->1}f(x)=0 - функция бесконечно мала в точке k, если существует такой предел.
Что тебе тут еще не понятно?
алсо, нахуй ты отдельный тред создал, есть аж два треда для начинающих, блядь.
Идио мамка твоя, долбоёб ебанный, в рот тебя ебал, хуесосина блядская, пидорасина чернушная, хуеглотина пиздлявая.
Таких точек бесконечное количество.
Каких "таких"? Либо выражай свои мысли полными предложениями, как белый человек, либо иди нахуй. Хули я угадывать должен, что ты там имел в виду? Точек, где функция бесконечно мала, может быть бескоечное количество, да - у тебя на твоем сайте написано об этом.
lim{x->k}f(x)=0 к тому же
Покажите мне такую точку на графике функции y=x, точку в которой y бесконечно мала.
Сама эта фраза "бесчконечно мала" уже подразумевает что это промежуток, а не точка.
я с обезьянами диалог не веду, это глупо, согласись
Фраза "бесконечно мала" ничего не подразумевает, она обозначает конкретную вещь в соответствии с определением. Я тебе его выше процитировал. Тебе нужно просто прочитать определение. Если предел функции эф от икс равен нулю при икс стремящемся в ка, то функцию называют бесконечно малой в точке ка. Что конкретно тебе не понятно в этом определении?
Чего блядь.
Да я уже все определения перечитал.
Если x стремится к точке k, тогда f(x) стремится к нулю, а если x=k, тогда y=0.
Мы говорим, что y бесконечно мала в точке k, но мы видим, что y=0 в точке k.
А бесконечно стремится к нулю не равно НОЛЬ!
Ладно, забыли, половина математики не верна. Сплошная теория кругом.
> перечитал
Теперь осталось вникнуть.
> если x=k
Где в определении хоть слово про равенство? Ты просто не понимаешь, что такое предел. Про то, что функция не должна существовать в точке, чтобы иметь в ней предел, в твоей статейке тозе написано. Короче, прочитай для начала ее до конца, потом постарайся запомнить определение, потом постарайся понять, что такое предел, а потом просто мысленно заменяй слова "бесконечна малая в точке ка" на "имеет предел, равный нулю, при икс стремящемся в ка".
/тхреад
Речь идет о функции, а ты пытаешься подменить функцию точкой. Но функция это не точка, это множество точек.
На картинке сказано: 0 - предел функции y в точке k
Или: 0 - предел функции при x->k.
Или: x стремится к k, а y одновременно стремится к нулю.
Больше там ничего не сказано.
Что такое k? Если x->k, значит k - одно из возможных значений x и лежит точка k строго на оси X. А так как у нас 2 оси тогда точка k имеет координаты (k,0).
И если x когда-то вдруг станет равен k, тогда y тут же станет равен 0.
Вроде пока никаких вопросов.
Наша функция y бесконечно мала в точке k (k,0).
И я даже знаю чему она в ней равна.
Не понятно, как может функция быть бесконечно малой в точке, в которой она чётко ноль.
Или: 0 - предел функции при x->k.
Или: x стремится к k, а y одновременно стремится к нулю.
Больше там ничего не сказано.
Что такое k? Если x->k, значит k - одно из возможных значений x и лежит точка k строго на оси X. А так как у нас 2 оси тогда точка k имеет координаты (k,0).
И если x когда-то вдруг станет равен k, тогда y тут же станет равен 0.
Вроде пока никаких вопросов.
Наша функция y бесконечно мала в точке k (k,0).
И я даже знаю чему она в ней равна.
Не понятно, как может функция быть бесконечно малой в точке, в которой она чётко ноль.
>Что такое k? Если x->k, значит k - одно из возможных значений
Обоснуй этот момент.
О чём с вами говорить, если вы даже этого не понимаете :)
Функция бесконечно мала в двух точках в k1(1,0) и k2(2,0) и равна она в них нулю.
Но этого просто не может быть. И всё дело в том, что она не бесконечно мала в этих точках.
>от Зорича до Шварца
Абсолютно идентичное мехматоговно, другого ты и не видел, похоже.
Проиграл с дебила не знающего определений.
>О чём с вами говорить, если вы даже этого не понимаете :)
в каких точках бесконечно мала 1/x?
>И всё дело в том, что она не бесконечно мала в этих точках.
Почему же нет?
На R в никаких, на PR в бесконечно удалённой.
А эта гипербола в каких точках бесконечно мала? Это просто глупый вопрос.
Если это реальная бесконечность, то там никакой конечной точки и не будет никогда в реале, а будет только бесконечный процесс стремления к нулю.
Направление стремления вместо точки.
Она не бесконечно мала в этих точках, потому что она в них чётко НОЛЬ. А ноль это не бесконечно малое. Точка - не направление стремления.
Раньше, видимо, этого не понимали, хотя лично я и раньше бы понял.
Прекрасные научные открытия. Нужно только обозначить их формальным языком, используя определения.
Если гипербола в окрестности ∞ не является бесконечно малой, то это означает, что ее предел не равен 0. Осталось это формально доказать.
Зачем? В физике ошибок ещё больше, даже у Эйншейна и всем плевать, хотя все, кто соображают, знают, что он напортачил.
А квантовая чего стоит. Это же вообще.
Находить ошибки в чужих теориях - это работа для неудачников.
Кроме того, за бесконечно малые я взялся, когда нашёл ошибку в производной, где мы тангенсы разных углов приравниваем, а за производную взялся, когда нашёл ошибки у Минковского с его пространством и мне не понравились преобразования Лоренца, чем я занялся, из-за того, что нашёл ошибку в СТО у Эйнштейна, а соответственно и в ОТО.
а этот человек:
вообще ни коим боком к открытию.
что за бред ты несёшь?
Если бред, то это надо опровергнуть. Опять же формально.
Проигрываю с треда, даже репортить это говно не буду
>в каких точках бесконечно мала 1/x?
>...в бесконечно удалённой.
>Если гипербола в окрестности ∞ не является бесконечно малой, то это означает, что ее предел не равен 0.
Вот скажи, ты, даун, за логикой диалога следишь хотя бы, или тебе просто спиздануть лишь бы что?
>На R в никаких
цитата. Хотелось бы доказательство этого факта.
блядь, там просто нет искомой точки ни в каких числах, ни в действительных, ни в каких других
вернемся сюда
>lim{k->1}f(x)=0 - функция бесконечно мала в точке k, если существует такой предел.
О какой точке идет речь?
Почему у тебя k стремится к 1?
Выучи матчасть для начала, ок?
x0 \in R / {0} lim(x->x0) 1/x = 1/x0 != 0
я тоже хочу такое определение предела (нет)
это не определение предела, а доказательство того, что в R/{0} не существует таких точек x0, что 1/x была бы бесконечно малой при x->x0.
Пределы - недопиленное говно, сугубо ИМХО.
а окрестности этих точек существуют.
да
Далеко не у всех функций есть предел. В этом нет ничего такого.
Пиздец, нахуй ты мне это говоришь?
> когда нашёл ошибку в производной
> нашёл ошибки у Минковского
> мне не понравились преобразования Лоренца
Не верю, что до меня, никто не говорил про неправильность бесконечно малых.
Так как обычно я оказываюсь далекое не первым, а переоткрывателем, хотя и сам дохожу с нуля, потом начинаешь гуглить и хоть вещи и редкие, но находятся.
Я вот даже думаю, что многие люди которые доходили до вещей, которые открыл и я они, про ни просто не говорили, может даже другим людям не говорили и записей не оставили.
Хотя бы то, что во Вселенной нет ни одного случайного события и быть не может и вся их "случайность" обусловлена лишь сложностью системы механизма "Вселенная", которую пока нереально расчитать и смоделировать будущее.
Так как обычно я оказываюсь далекое не первым, а переоткрывателем, хотя и сам дохожу с нуля, потом начинаешь гуглить и хоть вещи и редкие, но находятся.
Я вот даже думаю, что многие люди которые доходили до вещей, которые открыл и я они, про ни просто не говорили, может даже другим людям не говорили и записей не оставили.
Хотя бы то, что во Вселенной нет ни одного случайного события и быть не может и вся их "случайность" обусловлена лишь сложностью системы механизма "Вселенная", которую пока нереально расчитать и смоделировать будущее.
эта функция одна из таких, ясно же
пфф, ты не веришь?
давай я пороюсь в записях
У 1/x есть предел в каждой точке её области определения
Тут хоть есть "для чайников", по этому и спрошу здесь.
Куда пропал тред для начинающих?
Куда пропал тред для начинающих?
Пропажа треда для начинающих - первый вестник апокалипсиса, результатом которого станет пропажа всей доски.
ну что ж, исключения есть всегда, сам же понимаешь
Ты обдолбан что ли?
Для начинающих один тред, а для ищущих ошибки в трудах Великих - другие треды, причём каждая тема будет удостоена своего треда. Это справедливо.
Да я родился таким :) Но не прочь...
Можешь написать то, что раньше, только человеческим языком? Я про доказательство.
Святая Матрона прогнозировала конец света на 10 февраля 2017, то есть в эту пятницу.
Давай ты утверждение сначала сформулируешь.
Запилил для таких вопросов.
За какую теорию не берусь, везде ошибки нахожу, щито поделаешь.
Правда, недавно перепроверил теорему Пифагора и там всё норм.
Зато новую формулу для площади квадрата красивую нашёл
Sкв.=DR, не знал о ней раньше.
Ок. И в чём фишка, чем сложнее теория, тем меньше людей по ней прошли до тебя и тем ещё меньше людей её поняли.
Короче, вероятность найти ошибки в сложных навороченных тоериях, по истине огромна, в сравнении с теоремой Пифагора и подобными.
Правда, недавно перепроверил теорему Пифагора и там всё норм.
Зато новую формулу для площади квадрата красивую нашёл
Sкв.=DR, не знал о ней раньше.
Ок. И в чём фишка, чем сложнее теория, тем меньше людей по ней прошли до тебя и тем ещё меньше людей её поняли.
Короче, вероятность найти ошибки в сложных навороченных тоериях, по истине огромна, в сравнении с теоремой Пифагора и подобными.
Я про это
x0 \in R / {0} lim(x->x0) 1/x = 1/x0 != 0
1/x не является бесконечно малой в R
Ставьте Mathematica и не парьтесь больше, там всё 100% правильно.
https://www.youtube.com/watch?v=ozF5wKkXNjs
https://www.youtube.com/watch?v=jvpZWXkVjYQ
https://www.youtube.com/watch?v=JzWnl4eRiG0
https://www.youtube.com/watch?v=e6DpcS6M-Zg
https://www.youtube.com/watch?v=ozF5wKkXNjs
https://www.youtube.com/watch?v=jvpZWXkVjYQ
https://www.youtube.com/watch?v=JzWnl4eRiG0
https://www.youtube.com/watch?v=e6DpcS6M-Zg
Если простыми словами, то
Бесконечно малая это последовательность чисел которая находится между нулем и каким то наперед выбранным числом О, тобишь 0<бесконечно_малая<O.
Еще раз, бесконечно малая это не какое то конкретное число, это одновременно ВСЕ числа который между нулем и О. Почему? Потому что если бы это было конкретным числом, были бы числа больше и меньше его. Это следует из непрерывности действительных чисел. Любое число мы можем делить, скажем на десять, столько сколько хотим. У нас может кончится ручка, бумага, место на компьютере, место во вселенной для написания количества нулей, может закончится желание делить на десять постоянно, но чисто математически никаких ограничений нет.
Дальше, сложение, а следовательно и умножение потому что умножение это сокращенная запись сложения одинаковых чисел определенное число раз, бесконечно малых чисел на любое КОНЕЧНОЕ число будет давать в итоге бесконечно малую. Доказательство слишком длинное для написания, поэтому скажу так,
Если нужно умножить бесконечно малую на два что равно сложить два раза одну и ту же бесконечно малую то нужно брать все числа из последовательности которые меньше О/2, если на три то О/3, если на И то О/И.
С делением все сложнее. Деление это одновременно показатель на сколько частей, в делителях, можно разделить делимое, или если глянуть с другой стороны, сколько раз делитель влезает в делимое.
Так вот, если любое число делить на бесконечно малое будет бесконечно большое, так как из последовательности бесконечно малых мы можем взять какое угодно число чисел там, между нулем и О, бесконечно много как следует из непрерывности чисел.
Если же мы делим бесконечно малую на какое то число то в итоге получается опять же бесконечно малая грубо говоря 0.00000000001 делить на 100 будет нихуя не 10000000000000.
Однако, приведенные выше правила справедливы только если мы проделываем эти операции КОНЕЧНОЕ число раз.
Если же мы делим бесконечно малую на бесконечно малую может получится как бесконечно малая так и бесконечно большая так и ВНЕЗАПНО какое то конкретное число. На этом факте строится производная.
Если же мы суммируем бесконечно малые бесконечно большое число раз может получится опять же как бесконечно малая так и бесконечно большая так и ВНЕЗАПНО какое то конкретное число. На этом факте строится интегральное исчисление.
Если ты не совсем топологизировался в гомеоморфную гротендрику личность, то ты можешь заметить что просто так бесконечно малыми не пользуются. И правда, одна бесконечно малая плюс вторая дают в итоге опять же бесконечно малую. Используются они только как абстракции и вычислять с их помощью интегралы с производными можно только с помощью преобразования уравнений в которые входит бесконечно малая (x+бесконечно_малая)^2-x^2/бесконечно_малая=x^2+2x(бесконечно_малая)+(бесконечно_малая)^2-x^2/бесконечно_малая=2x+(бесконечно_малая)^2/бесконечно_малая=2x+бесконечно_малая=2х, по приведенным выше правилам производная квадрата в качестве примера. Пример с интегралом сложнее, так как придется использовать формулу сложения первых И квадратов из которой не вполне очевидно выходит интеграл квадрата x^3/3
Этих знаний тебе пока достаточно. Все это звучит сложно, хотя так оно и есть, но это намного удобнее калечных пределов.
Жду когда в меня начнут бурбакисты говном кидать из за того что человеческим языком объяснил, без множеств и жопоебли с очевидностями.
Как я уже говорил, искомой точки в данном случае вообще не существует ни в какой модели из бесконечного множества, описывающих реальный мир.
Но можете создать любую модель из другого бесконечного множества (ещё бОльшего) абсолютно с любыми законами, чтобы всё было, как вы хотите.
Я недавно создал гипотетический "Обратный Мир", где бесконечное количество всего, а обратные предметы - это дыры.
У обратных людей тоже есть свои античисла (отрицательные) обратные античисла итд.
Я рисовал разные варианты, пытался запихать их в одну систему, круг, прямая, вообще другие варинаты. Наш мир слева и их мир справа.
Я даже формулы написал для перевода туда и сюда.
Но от них нет толку, когда дело переходит к цифрам от буков, потому что 99999... (бесконечность девяток) ничего не даёт.
А один их обратный предмет это для нас inf -1 = 999... .
Короче, между нашими мирами аж две бесконечности.
Потом я понял, что чтобы совместить две разные системы, обе нужно расширить до более крупной системы и добавить механизмы взаимодействия. Но я боюсь, что в данном случае их расширять придётся бесконечно. Но это не доказано. Кто может доказать?
А кто может доказать, что бывают разные бесконечности и даже разные нули?
Подтверждаем.
Бурбаки
Я уже предполагал сегодня, что бесконечно малая это промежуток с бесконечным количеством точек, только ограничен он нулём с одной стороны и конкретной точкой либо бесконечностью с другой стороны в зависимости от функции.
Но первого общего варината, предложенного мной никто не отменял, он же и в конце у меня же и подвердился.
Бесконечно малая - это направление стремления, причём даже не вектор, так как длина промежутка чётко не определима и среди того бесконечного множества точек нет ни одной, которая бы удовлетворяла условие. Только точка в которой y=0 удовлетворяет условие, но эта точка выпадает из того множества, ведь, как я уже несколько раз говорил, мы бесконечно, сремимся к нулю, вместо того, чтобы просто взять да сделать y=0, потому что делать y=0 нельзя, т.к. это не будет бесконечно малая.
Короче, бесконечно малые - полное фуфло.
А в бесконечно больших ситуация ещё хуже, там даже нет точки, к которой мы можем бесконечно стремиться.
nu ti i down pizdec
скорее ты, ведь ты неконструктив, ты даже ничего опровергнуть не в состоянии, как и доказать свою точку зрнения.
Бесконечно малая (в точке к) - это функция, предел которой равен нулю при стремлении икс в к. Я надеюсь, что ты троллишь.
то что ты down не нуждается в доказательствах, это очевидно
Ладно, я для особо одарённых повторю.
Картинка не от примера, но подходит для понимания.
У нас есть точки пересечения функции с осью x, несколько штук x1, x2, x3. Все лежат на оси X, ни выше, ни ниже.
Точка (Координаты)
(Координаты): (x,y)
x1 (x1,0), x2 (x2,0), x3 (x3,0).
К этим точкам x стремится в пределах.
Теперь наш предел:
lim{x->x1}f(x)=0
0 - предел функции f(x) в точке x1 (x1,0).
f(x) - бесконечно малая функция в точке x1 (x1,0).
С x2 и x3 анлогично.
Ну так вот, функция f(x) является бесконечно малой в трёх точках – в точках x1, x2 и x3. Т.е f(x) бесконечно стремится к 0 в этих точках.
Запишем координатами эти три точки: (x1,0), (x2,0), (x3,0).
Итак, y=0 во всех трёх точках.
Но y - это же функция f(x) и y=f(x), т.е. функция во всех трёх точках равна строго нулю, не выше него и не ниже.
Но до этого мы писали, что функция является бесконечно малой в этих трёх точках.
А бесконечно малая не есть ноль.
Картинка не от примера, но подходит для понимания.
У нас есть точки пересечения функции с осью x, несколько штук x1, x2, x3. Все лежат на оси X, ни выше, ни ниже.
Точка (Координаты)
(Координаты): (x,y)
x1 (x1,0), x2 (x2,0), x3 (x3,0).
К этим точкам x стремится в пределах.
Теперь наш предел:
lim{x->x1}f(x)=0
0 - предел функции f(x) в точке x1 (x1,0).
f(x) - бесконечно малая функция в точке x1 (x1,0).
С x2 и x3 анлогично.
Ну так вот, функция f(x) является бесконечно малой в трёх точках – в точках x1, x2 и x3. Т.е f(x) бесконечно стремится к 0 в этих точках.
Запишем координатами эти три точки: (x1,0), (x2,0), (x3,0).
Итак, y=0 во всех трёх точках.
Но y - это же функция f(x) и y=f(x), т.е. функция во всех трёх точках равна строго нулю, не выше него и не ниже.
Но до этого мы писали, что функция является бесконечно малой в этих трёх точках.
А бесконечно малая не есть ноль.
Короче, f(x) в точке k (при x=k) равен нулю, а стремится f(x) к нулю только пока x не равен k!
Теперь, всем всё понятно?
Теперь, всем всё понятно?
Я думаю все уже посмеялись над этим клованом, тредж пора закрывать
Почему ты гадишь на математической доске в серьёзной теме? Мало тебе вконтактиков?
Твоё качество как человека бесконечно мало, так видят другие, а на деле оно = ноль.
Ты в своих постах только оскорбляешь и читаешь стандартное определение из учебника, из чего можно сделать довольно вероятный вывод, что ты вообще не понимаешь о чём мы тут целый вечер говорим.
Ясно.
Нахуя я только распинался, написал бы сразу в оппосте что ты дурачек и зашел потролировать матх.
Напиши, какие посты твои, чтобы их никто не читал, пожалуйста.
Зато твои посты прочитал я. Узнал много нового, спасибо.
не оп
Достаточно подставить эти точки k в функцию и сразу получаешь f(x)=0, строго равно нулю, но называется это почему-то f(x) - "бесконечно малая функция в точке k".
Какая она бесконечно малая, если она ноль?
Я думаю, когда-то кого-то запутал предел и он совершил небольшую ошибку, ну может ночью работал, кто его знает, а потом другие без понимания дела повторили его ошибку.
Какая она бесконечно малая, если она ноль?
Я думаю, когда-то кого-то запутал предел и он совершил небольшую ошибку, ну может ночью работал, кто его знает, а потом другие без понимания дела повторили его ошибку.
Что он такого умного мог тебе рассказать, если он не понимает, даже этого ?
Он тупо зубрила, который не понимает, что он учит, а ты лучше накачай больше разных учебников и посмотри ролики на ютубе, так гораздо лучше поймёшь математику, чем со слов зубрилы-неадеквата, который сразу в штыки, когда не может понять очевидные вещи.
На том сайте написано:
"в точках «плюс бесконечность» и «минус бесконечность»" дальше статью можно не читать. ИМХО.
"в точках «плюс бесконечность» и «минус бесконечность»" дальше статью можно не читать. ИМХО.
Мне кажется, что Вы докопались до мелочи.
В которой, кстати, ничего противозаконного не вижу: пополненная точками действительная прямая.
Вообще-то используется в языках программирования, чтобы корректно обрабатывать исключения в операциях с числами.


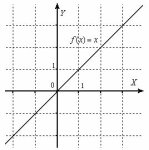









Единственная точка, которую я там вижу это ноль, в ней функция максимально мала по модулю, но если растянуть удовольствие и вместо точки взять направление стремления, да ещё и бесконечное (т.к. функция бесконечно мала), тогда мы получим ту же хреновину, какой является бесконечность и точка ноль не достигается никогда, кроме того, бесконечность вообще не точка, а только "стрелка", куда идём и всё.
Но ведь написано же:
"Функция может быть бесконечно малой или бесконечно большой только в конкретной точке."
http://mathprofi.ru/beskonechno_malye_funkcii_zamechatelnye_ekvivalentnosti.html
Берём его пример:
y=x^2-3x+2 y=0 при x=1 и при x=2
Конкретно при таких x, y=0.
А если x конкретно не равен 1 или 2 и пусть даже и очень близок, то это не 1 и не 2 и y в тех точках не ноль.
Если x бесконечно стремится, но так никогда не достигает 1 и 2, то и y никогда нулём не станет.
Выходит, что мы не может записать это в виде предела, в котором x -> 1 или x -> 2 и поставить "= 0", единственно верное условие x=1 и x=2 для y=0 и только.
На самом деле x легко принимает значения 1 и 2, функция в них не бесконечно мала, а просто равна нулю.
Почему тогда это называется "функция бесконечно мала"?