Хороший тред.
Есть ещё одна интересная задача.
Есть ещё одна интересная задача.
>пучк
Что?
Синусы плотны на окружности, следовательно, постоянно будут оказываться возле нуля. Ответ 0.
Нуль хуле. Модуль каждого синуса меньше 1 при натуральных N. Дальше элементарно доказать, что такая последовать носить стремится к 0.
>Модуль каждого синуса меньше 1 при натуральных N
И что из этого следует?
можно подробнее?
1>|sin(n)|>0
|sin(1)sin(2)...sin(n-1)|>|sin(1)sin(2)...sin(n-1)sin(n)|>0
Не знаю. Откуда?
Из этого ничего не следует, повторюсь. Попробуй посчитать предел у произведения e^{-1/n^2}. Они тоже все строго меньше единицы.
Рассмотри sin(n). Эта последовательность плотна на [-1,1] (это все знают). Следовательно, для любого \eps будет существовать N, такое что |sin(N)|< \eps. Отсюда, |sin(1) sin(2) ... sin(N)|<\eps. Следовательно, предел 0.
Забавное задание, кстати. Скинь еще чего-нибудь.
Если бы для каждого 0 < d < 1 в интервале (-d,d) было бы лишь конечное множество членов последовательности {sin n}, то было бы |sin n| -> 1, что, как легко проверить, неправда. Поэтому для некоторого d имеем |sin n_k| < d < 1, для некоторой подпоследовательности {n_k } натурального ряда. Дальше просто:
|sin1...sin n| < |sin n_1 ... sin n_k| < d^k -> 0
Тут k - любое, такое что n_k < n
>Рассмотри sin(n). Эта последовательность плотна на [-1,1]
Я вот не знал, пытаюсь доказать теперь.
Это не тривиальный факт. Вот объяснение: http://www.mathstat.concordia.ca/faculty/pgora/m364/Density.pdf
здорово, спасибо. красивое решение
>Из этого ничего не следует, повторюсь.
Из этого следует, что каждый следующий член меньше предыдущего(последовательность убывает). Но убывать до бесконечности она не может, ограничение 0.
С чего ты взял, что 0 - это самое нижнее ограничение? Я привел тебе пример: рассмотри последовательность таких произведений
e^{-1} e^{-1/2^2} e^{-1/3^2} ... e^{-1/n^2}. В ней каждый следующий член меньше предыдущего и ограничение снизу 0. Но предел равен e^{-\pi ^2 /6}
>самое нижнее ограничение
Я хотел сказать лучшая нижняя оценка
Ты прав.
В который раз убеждаюсь, что на этой доске сидят только умственно отсталые. С такими задачами вам в /un/.
sin(pin)=0; [10^npi]->10^npi при n->infinity; [10^npi] \in N; из всего этого следует, что последовательность sin([10^npi])->0 при n->infinity; обозначим через {Xk} исходную последовательность без членов вида [10^npi]; так как для любого x sin(x) \in [-1, 1], то она ограничена, т.к. sin([10^npi])->0 при n->infinity, она бесконечно малая, исходная последовательность есть произведение {Xk} и sin([10^npi]), произведение б/м на ограниченную -- б/м => предел исходной последовательности 0. Вы вообще тупые бараны?
sin(pin)=0; [10^npi]->10^npi при n->infinity; [10^npi] \in N; из всего этого следует, что последовательность sin([10^npi])->0 при n->infinity; обозначим через {Xk} исходную последовательность без членов вида [10^npi]; так как для любого x sin(x) \in [-1, 1], то она ограничена, т.к. sin([10^npi])->0 при n->infinity, она бесконечно малая, исходная последовательность есть произведение {Xk} и sin([10^npi]), произведение б/м на ограниченную -- б/м => предел исходной последовательности 0. Вы вообще тупые бараны?
Сука, звёздочки превращают текст в курсив. Не знал. Ну, думаю, и так всё понятно. В выражениях 10^npi между n и pi умножение, и естественно с обычным приоритетом (не в степени npi, а десять в степени n умножить на pi)
>Ну, думаю, и так всё понятно
Нет, вообще ничего не понятно.
Надеюсь, это троллинг. Между n и pi всегда ставь умножение, лол. Или тебе доказательство не понятно? Где конкретно? Да и если оно тебе непонятно, то советую открыть учебник, хотя бы самый простой.
Начиная уже отсюда
>[10^npi]->10^npi при n->infinity;
Что здесь написано вообще?
В квадратных скобках обозначается целая часть.
Смысл в том, что последовательность [10^npi] приближает последовательность 10^npi, а так как для синуса похуй, что 10^npi, что pi, то sin([10^npi]) приближается к sin(pi) при n->infinity, при этом [10^npi] всё-равно остаётся в N.
Это не правильно. Кек. Чёт тупанул. Всё, можете ссать мне в лицо.
ан нет, всё правильно.
net, не правильно, вообще. перерешаю щас.
>В квадратных скобках обозначается целая часть.
это надо пояснять. почему читатели должны догадываться?
>[10^npi]->10^npi при n->infinity;
эта запись -- бессмыслица
>Смысл в том, что последовательность [10^npi] приближает последовательность 10^npi
Что это значит?
>синуса похуй, что 10^npi, что pi
что-то осмысленное
>sin([10^npi]) приближается к sin(pi) при n->infinity
Почему?
Идея в общем-то похожая.
Короче, из последовательности натуральных чисел можно выделить такую подпоследовательность {Xn}, что для любого e>0 существует N: для любого n>N => (Xn/pi-[Xn/pi])<e. То есть, существует такая подпоследовательность последовательности натуральных чисел, что разность между kPi для некоторого k (его существование очевидно) и Xn стремится к нулю. Дальше всё как в предыдущей попытке. Вот это точно верно.
Конечно, стоит обосновать, что такая {Xn} существует, но это тривиально следует из того, что Pi содержит все возможные конечные цепочки цифр, включая цепочки нулей, тогда {Xn}={10^Rn}, где Rn -- количество цифр после запятой до первой цепочки из n нулей, но большее, чем R(n-1). Это свойство числа Pi опять же нужно доказать, но я оставлю его как известную теорему, потому что можно обойтись и без этого свойства, но тогда доказательство существования {Xn} будет длиннее.
Короче, из последовательности натуральных чисел можно выделить такую подпоследовательность {Xn}, что для любого e>0 существует N: для любого n>N => (Xn/pi-[Xn/pi])<e. То есть, существует такая подпоследовательность последовательности натуральных чисел, что разность между kPi для некоторого k (его существование очевидно) и Xn стремится к нулю. Дальше всё как в предыдущей попытке. Вот это точно верно.
Конечно, стоит обосновать, что такая {Xn} существует, но это тривиально следует из того, что Pi содержит все возможные конечные цепочки цифр, включая цепочки нулей, тогда {Xn}={10^Rn}, где Rn -- количество цифр после запятой до первой цепочки из n нулей, но большее, чем R(n-1). Это свойство числа Pi опять же нужно доказать, но я оставлю его как известную теорему, потому что можно обойтись и без этого свойства, но тогда доказательство существования {Xn} будет длиннее.
1. О чём догадываться? Это общепринятое обозначение.
2. Для любого e>0 существует N: для любого n>N =>
([10^npi]-10^npi)<e, действительно, надо было в фигурные скобки брать. Да и это не правильно оказалось.
3. В пункте 2.
4. ))
5. Опять же, признаю неправоту. В следующем посте исправленная версия.
>1. О чём догадываться? Это общепринятое обозначение.
Общепринятое обозначение -- это число \pi. А операция взятия целой части встречается слишком редко, чтобы для неё было общепринятое обозначение, кроме того, квадратные скобки "общеприняты" для множества других вещей. Поэтому таки приходится догадываться.
>В следующем посте исправленная версия.
Там тоже непонятно. Во-первых, утверждение
>существует такая подпоследовательность последовательности натуральных чисел, что разность между kPi для некоторого k (его существование очевидно) и Xn стремится к нулю.
очевидно неверно, т.к. kPi = const (если формально читать, что написано)
Во-вторых, сомнительное утверждение
>из последовательности натуральных чисел можно выделить такую подпоследовательность {Xn}, что для любого e>0 существует N: для любого n>N => (Xn/pi-[Xn/pi])<e.
требует тщательной проверки.
>Это свойство числа Pi опять же нужно доказать, но я оставлю его как известную теорему
Пожалуйста, ссылку, если можно
Простите, что лезу со своим сельским умом в /math, но я хочу спросить. sin(360+πn)=0 не может послужить тут обоснованием того, что пределом будет 0?
Тут до тебя уже два решения выложили, так-то.
блин, мечтаю понимать, как такое решать. Или хотя бы понимать, что там перемножается
блин, гениально. Я аж проиграл от того, как же это очевидно, чёрт возьми. И какой страшной эта задача казалась
Предел произведения можно делить на пределы множителей, если они конечны. Там может неопределённость получается. В целом, твоё рассуждение - подчасть доказателства.
Также не понял.
Идите нахуй
Доказать можно так: возьмем модуль от этого говна. Перемножение модулей а) ограничено нулем снизу и б) монотонно убывает(как было верно замесено, синус натурального строго меньше 1).По теореме вейерщтрасса имеет место предел.
Я не знаю, откуда эта задача. Подскажите залётному
Молодец, а еще он не меньше нуля. И че дальше?
И всё.
Задача решена.
Так то нет, это доказывает только что предел существует и не меньше нуля.
Вероятность равна нулю.
Если 9 из 10 на своих местах, то последнему письму негде оказаться, кроме как в своем конверте.
Там надо предел вычислить.
Верно.
Нуебанаврот, из строгого убывания же очевидно.
Ладно, давайте поиграем в формализм.
Построим систему из интервалов (a_n, b_n), пикрелейтед. По лемме о вложенных интервалах из первого семестра матана следует, что существует единственная лямбда, удовлетворяющая всем интервалам. И она, очевидно, строго меньше ебиницы. Промажорируем наше произведение синусов степенью этой чиселки. По скольку она фиксированна и строго меньше единицы, ее предельная степень это ноль. чтд
Абля. Еще надо рассматривать произведение модулей синусов.
вроде бы если писем бесконечность, то там получится вероятность e
рисуешь график, считаешь
Ты про беспорядки, говоришь. Но здесь по другому. Вначале тоже про них подумал.
Интересно какое обобщение графиков?
Блять, вот тебе ебучая последовательность, которая тоже строго убывает, положительна и к нулю не стремится: 1488 + 1/n.
В твоем втором решении нихера не очевидно, что лямбда меньше единицы (на самом деле, она РАВНА единице, потому что синусы натуральных плотны на отрезке [-1, 1])
Мне очевидно только то, что ты обосрался. Дважды.
Лямбда нихуя не равна единице, поскольку она принадлежит объединению интервалов. Она строго меньше единицы.
Говорит что лямбда равна 1 равносильно утверждению, что 0.(9) = 1
Пизда.
>объединению
Пересечению же.
А такой тред был хороший...
А нельзя сказать просто что она во-первых убывает, а во-вторых имеет бесконечное число положительных и отрицательных знаков, поэтому ноль?
Ну и к тому же имеет предел по какому-нибудь признаку.
Если ты имел в виду "убывает по модулю", то нельзя. Вот контрпример: (-1)^n + (-1)^n/n.
Там выше два решения лежат.
У тебя правый конец закреплен, так что ты не доказал, что /lambla строго меньше единицы.
Для любого L < 1 найдется такое n, что sin(n) > L, т.к. sin(n) плотен на отрезке [-1;1]
Класс! Про плотность не додумался.
Вот вы говорите: синусы. Пределы. Но позвольте...разве это математика?
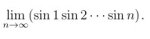










Предлагаю в этом треде решить её, а также, может быть, и остальные 99