МАТЕМАТИКА ДЛЯ НАЧИНАЮЩИХ, ТРЕД 23: Высшая математика для физиков и техников Аноним OP 29/11/16 Втр 14:00:30 #2 №4137
Блять, проебал название. Мод, если можешь то поправь, плиз.
Сколько времени в процентах тратить на изучение теория/практика?
Индивидуально.
Это снова я, как лучше организовать сам процесс обучения? Записывать ли теорию в тетрадь или сделать отдельные тетеради для теории и практики? Вообщем любые советы помогут.
Сап, помогите с построением ИВ вывода с помощью Аксиом ИВ(система Клини).
Не знаю, как начать
1) посылка
2) ....?
Не знаю, как начать
1) посылка
2) ....?
Добавь Ткачук - Математика абитуриенту (17-е издание М:МЦНМО 2017) в ОП список 2
напиши в ди
алсо, соус учебника с оп пика?
>Высшая математика для физиков и техников
Я обычно все в 1, однако под решения вывожу отдельно страницу и сверху подписываю "Страница-черновик", непосредственно ответ в явном виде выделяют (обвожу). Если подряд задачи и теоремы выписывать получается нечитабельное невесть что.
Сап, Двач! Такая дилемма: в программе Воркбенч надо сделать шифратор в базисе и-не, на входе десятичный код, на выходе 7421, дешифратор в базисе или-не, на входе - код с избытком 3, на выходе - десятичный и преобразователь кодов в базисе и-или-не, на входе - с избытком 3, на выходе - 7421. Скрины ооочень даже нужны (всего должно быть 15 штук). Даже если ты это читаешь и начинаешь тихо про себя материться, то я не прошу делать это все за меня а просто объяснить, как и где, тащемна. Программа есть, литература есть, но все равно нихуя не смыслю. Буду очень благодарен и приглашу на чай с печенькой. Извиняюсь за флуд, в прошлой теме на заметил ссылки на новый трэд
Алсо, сборник матпрограмм (включая вербитскую, но без второй)
http://mathcenter.spb.ru/nikaan/knowledge.html
я когда-то в этом кружке учился, кстати, потом понял, что олимпиады для аутистов и съебал в первую культуру
Сложна, нужны азы изучения алгебры-логики
тебе, наверное, в /pr
Окай(
Установи в браузер change font и горя не знай, либо купи телефон на андроиде.
Не, я могу в принципе потерпеть. Просто не ожидал увидеть этот шрифт там.
Есть кто живой ? Срочно нужна помощь по решению примеров
Каких?
сообщение потерли, лол. нужно найти производные функций
И что мешает тебе их найти?
Как определить уравнение касательной к кривой, которая касается этой кривой в неизвестной точке и пересекает график в заданной точке?
Там, вроде-бы уравнение пучка или что?..
Угловой коэффициент касательной неизвестен по причине того,
что неизвестны координаты точки касания,
и как следствие - значение производной в этой точке.
А чтобы выразить угловой коэффициент из уравнения прямой,
нужно хотя-бы две точки, через которые проходит эта прямая.
Ну то, что я из математики запомнил только таблицу умножения, а этого мало. Ах да, я гуманитарий.
Смотри таблицу производных/правил дифференцирования. Там всё просто.
алсо, программа олимпиадника от него же
https://web.archive.org/web/20090102065543/http://mathcenter.spb.ru/nikaan/problems/need_olymp.txt
http://knop.livejournal.com/116971.html
Блеванул. Мантру "группы, кольца, поля" из 1920-х уже давно пора заменить на "модули, идеалы, кольца, алгебры".
это программа для школьников, остынь
>новые результаты
>алгоритмически разрешимая программно задача
ой насмешил ирод
Я тебе уже ответил, пидор, два уравнения.
>угловой кооф.
Он у тебя уже есть, ты же касательную проводишь, он равен f'(точки).
помогите пожалуйста понять ошибку в моём решении, есть определенный интеграл, и результат моего решения этого интеграла не сходится с решением wolfram alpha, я не могу понять, почему, объясните пожалуйста, по-моему, дело в чём -то совсем элементарном
http://www.wolframalpha.com/input/?i=((2%2F(sqrt(a))-2)%2Fn+%3D+(2-2sqrt(a))%2F(nsqrt(a))
Кто этот математик?
Помогите пожалуйстаа
Помогите пожалуйстаа
Heisenberg?
You goddam' right.
спасибо
бамп
бля, оу пи, ты какие-то хуевые темы для трэдов подбираешь,
я же тебе говорил, что рецепт хорошего начинайко трэда - это мейнстрим
а ты все свое затираешь, то виленкина, теперь зельдович, складывается ощущение, будто ты школьник или другой вид быдла, которой, что сам читает, то в тему и сует
я прав?
алсо, ты игнорируешь предложения по хорошим книгам и вообще хуй положил на пастебины, такими темпами твои перекаты скоро станут нелегитимными, задумайся
а иначе перекатывать придется более инициативной личности
я, кстати, начал пилить стикерпак с гротендиками, вербицкими итд, кому похуй - тому похуй, ныть не надо тут
лишним точно не будет, можете оставлять свои пожелания здесь, или я даже могу временную тему под него создать
Создавай, этот тред про другое все-таки.
никак не получается решить, помогите. Я совсем нуфаг в интегралах уровня час. Не получается даже привести к табличным, всё время выходит длинная дичь.
Посоветуйте годные учебники и задачники по математике, в которых все понятно написано и разжевано для курса 8-9, 10-11.
ты точно выражение выписал?
объясните пожалуйста понятие равномерной непрерывности функции на словах, а то что-то мне не понятно это определение, и приведите пожалуйста пример такой функции, которая является непрерывной, но не является равномерно-непрерывной
значит как бы сильно не выебывался аргумент, функция бы не выебывалась сильнее. Например, парабола на R с чертой всегда выебывается круче, чем ее аргумент.
я не понимаю всё равно, объясни пожалуйста как-то по другому, и что такое R с чертой, множество действительных чисел? Тогда что за черта?
R с чертой = R U {+-бесконечность}
значит ты берешь некую окрестность выебывания икс (дельту) и говоришь: игрек должен выебываться в окрестности не сильно круче икса (эпсилон от дельты). Потом проверяешь всю функцию на эту тему, если она проходит проверку, она равномерно непрерывно.
для y=x^2, например, ты берешь такую окрестность (x;x+e/x), а он её где-то все равно нарушает (это можно проверить, если рассмотреть предел разности функции на концах отрезка).
то есть если x изменяется в пределах дельты, то игрек должен изменяться в пределах эпсилон, так?
А как проверить функции на равномерную непрерывность, которые заданы на всей прямой R с чертой, на ней будет функция x^2 равномерно-непрерывной?
> (это можно проверить, если рассмотреть предел разности функции на концах отрезка).
давай-ка сам.
f(x)=x^2
f(x+e/x)-f(x)=?
Раз у нас есть бесконечность, то можно устремить туда икс (найти предел).
Но заметь, требование открытого отрезка принципиально, иначе по теореме Кантора-Гейне функция будет равномерно-непрерывной. Например, попробуй найти такой эпсилон, чтобы проверить x^2 на [+1;+25]
Если ты понимаешь определение непрерывности, то просто мысленно запрети дельте зависеть от аргумента функции а то обычно-то зависит, если что. Получишь определение равномерной непрерывности = везде одинаковая непрерывность, в любой точке рассматриваемой области определения.
А про Кантора очевидно же. Можно просто выебон функции ограничить числом max-min, суть примерно такая
>угловой кооф.
Писать научись для начала.
>он равен f'(точки)
Да-да, неизвестной точки.
>два уравнения
Для уравнения прямой между точкой касания и точкой пересечения - нужно две точки, а координаты точки касания - не известны.
>Я тебе уже ответил
Это даже ответом не является
>пидор
Берешь в качестве неизвестного точку, в которой касательная проводится к функции.
Уравнение касательной к функции f в точке x_0 выглядит как (1).
Если у тебя известная точка (x_0, y_0), то итоговое уравнение на неизвестную точку касания x выглядит как (2).
Одно уравнение на одну неизвестную. 8 класс
>Да-да, неизвестной точки.
x0
>нужно две точки
У тебя есть одна из них, хуле тебе еще надо?
>x0
Эта её координата неизвестна.
>хуле тебе еще надо?
угловой коэффициент.
Вот, допустим, можно замутить уравнение пучка прямых с центром в точке пересечения касательной с функцией. Пик 3
>Берешь в качестве неизвестного точку, в которой касательная проводится к функции.
Ну, там две неизвестные: x и y;
>Уравнение касательной к функции f в точке x_0 выглядит как
И значит, там одни неизвестные...
>Если у тебя известная точка (x_0, y_0), то итоговое уравнение на неизвестную точку касания x выглядит как (2).
Да бля, это что тут получается?..
Такой, что-ли угловой коэффициент?
f'(x) = (f(x) - y_0)/(x0 - x);
Давай по новой. Итак, у тебя есть человек, назовем его Иван Иваныч. Тебе надо найти Ивана Иваныча среди многих людей. Ты знаешь, что Иван Иваныч носит шляпу. Ты знаешь, что Иван Иваныч спит с твоей мамкой.
Ты составляешь первое уравнение:
Люди, которые спят с моей мамкой. Перед тобой встает несколько толпа людей.
Ты составляешь второе:
Люди, которые носят шляпу. Перед тобой встает толпа поменьше.
Теперь ты составляешь систему: люди которые спят с моей мамкой И носят шляпу. И чудесным образом перед тобой встает Иван Иваныч собственной персоной. Однако, увидев число любовников твоей матери он несколько разочаровался в себе.
Теперь представь себе, что уравнение касательной это люди, которые касаются твоей кривой (мамки), ну ты понял. И ты знаешь, что люди носящие шляпу, проходят через определенную точку. Значит Иван Иваныч будет касательной, которая проходит через эту точку. Алгебраически это выглядит так:
По-моему тот анон уже три поста как пытается объяснить, что помимо Иван Иваныча там будет еще и Евгений Петрович, и Захарий Модельяныч, и еще целая толпа мужиков.
Вполне возможно, зависит от порядочности (порядка) его мамки.
И Иван Иваныча и Евгений Петровича, и Захария Модельяныча, и всех возможных рандомных Аноним ID из /po/литача.
>>4283 ->
Первое уравнение - одни неизвестные.
f'(x) - тоже неизвестное, которое зависит от двух неизвестных, x и y;
Пусть, например, кривая будет эллиптической с уравнением
y^2 = x^3 + 100;
И пусть, f'(x) = 3x^2/2y;
Второе уравнение с тремя неизвестными,
зависящее от одной неизвестной.
>ты составляешь систему
И получаешь за это шайбе.
Первое уравнение - одни неизвестные.
f'(x) - тоже неизвестное, которое зависит от двух неизвестных, x и y;
Пусть, например, кривая будет эллиптической с уравнением
y^2 = x^3 + 100;
И пусть, f'(x) = 3x^2/2y;
Второе уравнение с тремя неизвестными,
зависящее от одной неизвестной.
>ты составляешь систему
И получаешь за это шайбе.
Привет всем из dxdy
Есть функция двух переменных. Есть ли аналитический способ, которым можно установить, дает ли функция замкнутую траекторию?
а что такое е? это основание натурального логарифма? А открытый отрезок это что такое?
e это эпсилон в данном случае, просто некая переменная.
>открытый отрезок
это такой отрезок каждая точка которого содержится в неком открытом шаре с центром в этой точке. К примеру отрезок (0,1) открыт, а отрезок (0,1] нет, т.к. в точке 1 нельзя подобрать такой шар, т.е. нельзя найти ненулевой радиус (d(x,x)=0, по определению метрики в r).
>требование открытого отрезка принципиально, иначе по теореме Кантора-Гейне функция будет равномерно-непрерывной. Например, попробуй найти такой эпсилон, чтобы проверить x^2 на [+1;+25]
но если отрезок [+1,+25] не является же открытым, то есть его концы входят в отрезок, следовательно функция x^2 является равномерно-непрерывной, разве нет?
f(x+e/x)-f(x)=(x+e/x)^2-x^2=x^2+(2ex)/x+e^2-x^2=2e+e^2;
но я не понимаю, что из этого следует.
функция является равномерно-непрерывной на данном отрезке, все верно. Но одно дело сослаться на теорему, другое дело убедиться воочию.
>+e^2
+e^2/x, что бесконечно мало.
Остается 2e. Т.е. мы взяли отрезок e/x (дельту зависящую от икс), а функция в пределе подскочила аж на 2e, что больше чем эпсилон. По определению это означает, что мы нашли такую дельту, при которой условие будет нарушаться.
>функция является равномерно-непрерывной на данном отрезке, все верно. Но одно дело сослаться на теорему, другое дело убедиться воочию.
но я не понимаю, как убедиться в этом, как подобрать этот эпсилон. Объясни пожалуйста как.
>+e^2/x, что бесконечно мало.
но если возвести (x+e/x) в квадрат, то есть (x+e/x)^2=x^2+(2ex)/x+e^2=x^2+2e+e^2,
то там просто e^2, а не e^2/x, я не понимаю, откуда там x.
(x+e/x)^2=(x+e/x)(x+e/x)=xx+(e/x)x+x(e/x)+(e/x)(e/x)=x^2+2x(e/x)+(e/x)^2=x^2+2e+e^2/x^2
>но я не понимаю, как убедиться в этом, как подобрать этот эпсилон. Объясни пожалуйста как.
Нарисуй что-ли себе график. И ответь на вопрос, каким надо сделать дельту, чтобы обуздать функцию на этом отрезке.
Подвох для функции бесконечности в том, что какую бы мы дельту не брали, где-то там далеко, она все равно нарушит наше ограничение, вырастет еще сильнее.
>Нарисуй что-ли себе график. И ответь на вопрос, каким надо сделать дельту, чтобы обуздать функцию на этом отрезке.
я не понимаю, мне сначала надо выбрать дельту, а потом смотреть, как изменяется эпсилон(то есть эпсилон зависит от дельты), или же сначала выбрать эпсилон, а потом смотреть, в каких границах можно менять дельту, чтобы значение функции не менялось(то есть дельта зависит от эпсилон)?
Анон, помоги, диффур не поддаётся. Он не линейный, не однородный, значит, надо дифференциалы выделять. На одной картинке исходный диффур, на другой то, что у меня получилось выделить, но с последним слагаемым едва ли можно что-то сделать.
fix
откуда диффур взял?
взгляни на определение равномерно-непрерывной функции. если там написано "существует", то тебе необходимо предъявить то, что существует.
Домашняя работа.
Лень решать что-то, лол. Интегрирующий множитель пробовал искать?
у меня мэпл отказался эту хероту решать, даю зуб там опечатка какая-нибудь.
Ну, интегрирующего множителя, зависящего только от x и y, не существует. Это я сразу же проверил. Интегрирующих множителей вида x/y, x+y, x^2+y^2, x*y тоже вроде нет. Я не знаю, что ещё перебирать.
Обидно тогда.
>только от x или y
Математика вроде бы решила, но проблема в том, что она неявные функции не любит и из-за этого ответ получился в три строки.
спецфункции были?
Странно, DSolve решает, а DSolveValue - нет. Херовое уравнение, короче.
Вот такая вот херня, дальше никак не хочет.
Если ты имеешь в виду именно кривую, то и написал бы "кривую f(x, y) = 0"
Рассуждения на случай двумерного пространства
В таком случае тоже несложно: вектор градиента функции f вектор (f_x, f_y) есть нормаль к кривой (касательный вектор построить несложно (f_y, -f_x)). Даже если неизвестна точка касания (x, y), то на неё тогда можно составить два уравнения:
1. Точка принадлежит кривой
2. Касательная из этой точки проходит через заданную в условии точку (x_0, y_0)
И решай не 8й, 9й класс уже, ладно
в этот раз без теховских формул, пишу с свчшницы
а если кому интересны правдоподобные рассуждения, могу сказать простую вещь: можно эффективно рассуждать в терминах степеней свободы, помогает понять необходимое количество независимых уравнений на неизвестные
Для справки: в n-мерном пространстве у точки их n, у прямой 2n-1 (2 точки + 1 связь) и т.д.
Ты сам-то понял, что написал?
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)
- уравнение прямой, проходящей через две точки.
(x1, y1) координаты касания,
(x2, y2) - координаты точки пересечения между касательной и функцией.
y - y1 = k × (x - x1) - уравнение пучка прямых, проходящих через точку касания.
k = (y2 - y1)/(x2 - x1) - угловой коэффициент из уравнения прямой, проходящей через две точки.
y = f(x1) + f'(x1)×(x - x1) - уравнение касательной, в точке касания;
y - y1 = k×(x - x1); уравнение пучка прямых с центром в точке касания.
k = f'(x1) - угловой коэффициент касательной.
y1 = f(x1); ордината точки касания.
Если приравнять по угловому коэффициенту, получится:
f'(x1) = (y2 - y1)/(x2 - x1)
x1, y1 - неизвестные; x2, y2 - известные.
y1 = f(x1);
f'(x1) = (y2 - f(x1))/(x2 - x);
f'(x1)(x2 - x) = y2 - f(x1);
y2 - f(x1) = f'(x1)(x2 - x);
y2 = f(x1) + f'(x1)(x2 - x) - второе уравнение -
куна.
И в нём - две неизвестных, т. к. помимо x - неизвестна и x1.
Как его решать?..
Кто-то там курлыкал про системы уравнений, но некачественно как-то...
Этот, вроде-бы... Даже не читал особо его высер...
>И в нём - две неизвестных
Даже не две, а четыре.
x1, f(x1), f'(x1), x.
Так у тебя блять еще и функция неизвестна? Ну ты совсем охуел.
значение функции и её производной от неизвестного значения является зависимым неизвестным, поэтому иди уже нахуй
Есть ли ресурс аналогично problems.ru только по физике?
Пусть, например, кривая будет эллиптической с уравнением
y^2 = x^3 + 100;
f(x) = √(x^3 + 100)
И пусть, f'(x) = 3x^2/2y = 3x^2/2×(x^3 + 100);
Только вот что это даст?
>3x^2/2×(x^3 + 100)
Тут ещё и корень пихнуть надобно бы.
f'(x1) = 3x1^2/(2×√(x1^3 + 100))
А дальше - ваще ебень какой-то...
Короче, можно ли найти касательную не зная точки касания, или нет?
>А дальше - ваще ебень какой-то...
Ебень отклеился...
y2 - √(x1^3 + 100) = 3x1^2 (x2 - x)/2×√(x1^3 + 100) |× 2×√(x1^3 + 100)
2×y2×√(x1^3 + 100) - 2×(x1^3 + 100) = 3×x1^2×(x2 - x)
И всё-равно тут две неизвестные.
Где можно почитать, что значит индекс плюс или минус у икса или чего-либо еще?В моем случае там E((X-EX)+)
Сильно ли это отличается от записи без плюса или как перейти от обозначений с плюсом к обозначениям без них?
Сильно ли это отличается от записи без плюса или как перейти от обозначений с плюсом к обозначениям без них?
Так, короче это как я и думал =max(0,x), верно же?
>две неизвестных
могу тебе подсказать еще одно уравнение с двумя неизвестными:
Ax+By+C=0
возможно, наведет тебя на нужные мысли
Если касательная в точке пересекает график два раза - да, зная эти точки, и забив их в уравнение прямой.
спасибо, с функцией x^2 понятно. А в общем случае, как найти такую дельта? Например, если f(x)=x^(1/3), то как проверить эту функцию на равномерную непрерывность?
Чем отличается математика от арифметики?
Мылач, твоя помощь срочно нужна. Как такое решать?
При каких значениях к многочлен x^(2k)+1 делится на:
- x^5 +1
- x^3 +1
При каких значениях к многочлен x^(2k)+1 делится на:
- x^5 +1
- x^3 +1
Найти производную siny+cosy=x в значениях х
Нахожу dy/dx = 1/cosy-siny; как избавиться от y?
Нахожу dy/dx = 1/cosy-siny; как избавиться от y?
k = 1.5 и 2.5 очевидно же.
сорян, там при натуральных значениях надо. И важен сам способ решения
Гугли деление многочленов столбиком.
ну помогите же пожалуйста, как в общем случае проверять функцию на равномерную непрерывность на (-∞, ∞)? В случае с f=x^2 дельту надо брать равной e/x, а в общем случае как понять какую дельту надо рассматривать? Подбором? Какую дельту надо рассматривать в случае f=x^3 и какую в случае f=x^(1/3)? Они же не будут равномерно-непрерывными на (-∞, ∞)?
Может это тебе что-то даст?..
a/b = c + r
a = c×b + r; r = 0;
a = c×b
x^(2k)+1 = c×x^5 + 1)
x^(2k)+1 = c×x^5 + c
x^(2k)+1 = c×x^3 + c
x^(2k) - c×x^5 - c + 1 = 0
x^(2k) - c×x^3 - c + 1 = 0
c = x^y
x^(2k) - x^y×x^5 - x^y + 1 = 0
x^(2k) - x^(y+5) - x^y + x^0 = 0
Это - стандартное уравнение прямой.
Две неизвестных. Наводит только на фап-тред.
А там - хуй.
"Олимпиады для аутистов"?
Лол, пока аутист одну задачу решает уже время выйдет.
Лол, пока аутист одну задачу решает уже время выйдет.
Подбором. Можно, например, не подбирать точные значения, а давать им оценки, например, если одно число больше 1, а другое меньше, то они определенно не могут быть равны. Поищи какой-нибудь материал на эту тему.
>x^1/3
hint; она равномерно-непрерывна
Ты че? Как раз-таки наоборот. Аутисты могут на узкой задаче достигать концентрации внимания и усилий недоступных для нормального человека. Аутисты часто становятся выдающимися деятелями областей, где не нужно сложно взаимодействовать с людьми.
>hint; она равномерно-непрерывна
Откуда это известно?
т.е. не в науке
Давай покажу, как будет в твоём случае чет даже не лень стало
Уравнение кривой будет выглядеть как (1).
Вектор нормали в точке (x,y), принадлежащей этой кривой, будет вектором с координатами (2) вектор градиента в точке, или, другими словами, взяли частные производные по координатам, см. . Вектор касательной, соответственно, (3).
Проводишь прямую из точки (x,y) вдоль вектора (3). Ты должен попасть в известную по условию точку (x_0,y_0). Я выбрал параметрический способ задания прямой (4). Преобразовал, исключив параметр t, получил другой способ задания кривой (5).
А теперь ты имеешь два уравнения (1) и (5) на две, блять, неизвестные x и y. Если у тебя всё еще остались вопросы, то ты, блять, просто дебил неизлечимый.
И мне похуй, как ты эту систему решать будешь
> получил другой способ задания кривой (5).
Блять, описка. Прямой, в смысле той же касательной.
Ну еще картинку пошакалило чет, и да похуй.
Посоветуйте дауну что-нибудь по математическому анализу. Что-то вроде Зорича, но чтобы на пальцах.
Я - про уравнение касательной, и угловой коэффициент, а он мне про вектор нормали, про вектор градиента, про неизлечимый систему дебил похуй решать, про вектор касательной, про какую-то хуйню, малафью, шишка встанет, возбудимся, про что несёт вообще охуеть...
Курант Курс дифференциального и интегрального исчисления
Ну ты реально отбитый.
Касательная, как и любая прямая, может быть задана как точка+направляющий вектор. Зачем мне задавать прямую так, как мне неудобно?
Угловой коэф прямой также может быть вычислен как отношение координат вектора (второй к первой). Только нахуя оно надо?
Если даже такое понять не можешь, то пиздуй в 10й класс изучать производную заново.
Решение я тебе предложил, если не нравится — учи матчасть и придумывай своё.
Попробуй поискать курсы матана для школьников из какого-нибудь СУНЦ (ФМШ) МГУ/НГУ
только неебу как их искать
Оо, вот теперь понятно.
Понятно.
Как ты здесь исключил параметр t?
xy=t
x+y=t
помоги даше исключить параметр t.
Приравняй по t
>И мне похуй, как ты эту систему решать будешь
Положил функцию вместо y - ваще получил, уравнение 6-й степени.
>Как ты здесь исключил параметр t?
Да как угодно, лишь бы его не стало.
Варианты:
1. Выразить явно из одного уравнения t, подставить в другое.
2. Сделать коэфы при t одинаковыми в обоих уравнениях, вычесть из одного другое.
По своей сути они одинаковы: из двух уравнений делает одно ценой уменьшения количества неизвестных.
А по факту, эти рассуждения на уровне 1 курса матфака и понимания, что к чему в математике в целом.
Что за высер бесполезный, два предложения содержательных написать не может.
Но зато, на одну неизвестную.
Какую функцию-то положил? Если брать пример, разобранный в то там будет уравнение третьей степени максимум (хотя удобней решить уравнение второй степени относительно y (исключив x), потом подставить решения в первое уравнение и найти x).
Ну и да, поиск нужной касательной не легче поиска нулей функции, к примеру.
Ну, y^2 = x^3 + 100;
и y = √x^3 + 100;
3x^2⋅(x - x0) = 2⋅√(x^3 + 100)⋅(√(x^3 + 100) - y0);
3x^2⋅(x - x0) = 2⋅(x^3 + 100) - 2⋅√(x^3 + 100)⋅y0;
2⋅√(x^3 + 100)⋅y0 = 2x^3 + 200 - 3x^2x - 3x^2x0;
√(x^3 + 100) = (2x^3 + 200 - 3x^2x - 3x^2x0)/2y0;
А всё - в квадрат даёт 6-ю степень с правой стороны.
Числитель справа:
2⋅(x^3 + 100) - 3x^2⋅(x - x0) = 2⋅x^3 + 200 - 3⋅x^3 - 3⋅x^2⋅x0 = 200 - x^3 - 3⋅x^2⋅x0;
Квадрат числителя:
(200 - x^3 - 3⋅x^2⋅x0)^2 = (200 - x^3 - 3⋅x^2⋅x0)⋅(200 - x^3 - 3⋅x^2⋅x0) =
40000 - 200x^3 - 600x^2⋅x0
-200x^3 + x^6 - 3x^5⋅x0 - 600x^2x0 + 3x^5⋅x0 + 9⋅x^4⋅x0^2 =
40000 - 400⋅x^3 - 1200⋅x^2⋅x0 + x^6 + 9⋅x^4⋅x0^2;
Квадрат правой стороны:
(40000 - 400⋅x^3 - 1200⋅x^2⋅x0 + x^6 + 9⋅x^4⋅x0^2)/4y0^2;
И, вот такая вот поебнятина:
4⋅y0^2⋅(x^3 + 100) = 40000 - 400⋅x^3 - 1200⋅x^2⋅x0 + x^6 + 9⋅x^4⋅x0^2;
Геометрически, у кривой бесконечное число подпорок-касательных, а есть прямая на точке-шарнире, которая крутится вокруг своей оси. Так что нужно подобрать такой угол, чтобы прямая совпала с касательной. Прямая характеризуется углом, касательной точкой функции: две неизвестных. В чем сложность провести такое наивное рассуждение? Это 8-ой класс, первый курс матфака не нужен.
>Выразить явно из одного уравнения t, подставить в другое.
Да ну?
x + 2y⋅t = x0
t = (x0 - x)/2y
y + 3x^2⋅t = y0
t = (y0 - y)/3x^2
(y0 - y)/3x^2 = (x0 - x)/2y
(y0 - y) = 3x^2/2y ⋅ (x0 - x)
(y0 - y) = k⋅(x0 - x), k = f'(x) = 3x^2/2y; уравнение касательной в виде уравнения пучка прямых в точке касания.
Не совсем похоже на твоё (5)
Ой, тьфу, слегка попутал - это оно жи и есть.
(y0 - y)/3x^2 = (x0 - x)/2y;
2y⋅(y0 - y)/3x^2 = (x0 - x);
2y⋅(y0 - y) = 3x^2⋅(x0 - x);
3x^2⋅(x0 - x) = 2y⋅(y0 - y); (5)
это широко распространённое заблуждение одного идиота, впервые вижу
ты судишь по нескольким элеменам, о которых ты услышал, О ВСЁМ МНОЖЕСТВЕ
это признак идиотии
Ты не путаешь с Фихтенгольцем? Просто именно у Куранта книги с таким названием не нашел.
А давай я тебе скажу, что у тебя уже ошибка есть с точки зрения математики? Пытаться понять эти выкладки в таком виде нет желания совсем. Хоть бы тех распаковал, ну.
Она еще во второй строке. Когда решаешь уравнение вида x^2 = a, решение есть не только сам корень из правой части, а еще то же самое, но с минусом.
Но в целом, ты всё равно не понял, о чем я тебе толковал всё это время.
Не обязательно выражать y через x, так только в школе делают. Для решения задач с кривыми порядка выше первого стоит пользоваться более мощным аналитическим аппаратом, который предлагает матан/ангеом (подчеркни, что нравится).
Я показывал уже готовое решение для примера (система из уравнений 1 и 5 в ), в которое надо только подставить x_0 и y_0, после чего получить необходимые точки, в которых нужно провести касательные.
помогите пожалуйста с примером из функционального анализа, есть 2 пространства сходящихся числовых последовательностей, X=l_2, и Y=l_1, и задано отображение Fx. Необходимо ответить, является ли заданное отображение:
a) непрерывным;
б)равномерно-непрерывным;
в)удовлетворяющим условию Липшица;
Объясните пожалуйста, как проверить все эти условия, определения всех этих понятий выписаны, но я не понимаю, как их проверить на практике,
объясните пожалуйста алгоритм решения такого задания.
Поясните за ГРАССМАНОВУ АЛГЕБРУ.
Чо за хуиня, где про неё почитать и какие минимальные знания нужны для этого?
Чо за хуиня, где про неё почитать и какие минимальные знания нужны для этого?
>готовое решение для примера
>система из уравнений 1 и 5
>надо только подставить x_0 и y_0
>после чего получить необходимые точки
>в которых нужно провести касательные
Уравнение прямой предполагает однозначное определение координаты y, по известному x;
Подставив во второе уравнение известные значения x0, y0, выразить y нельзя.
Ты там раньше писал, что:
>удобней решить уравнение второй степени относительно y (исключив x)
Т. е. хочешь сказать, что:
3x^2⋅(x - x0) = 2y⋅(y - y0);
3x^2⋅(x - x0) = 2y^2 - 2y⋅y0;
и при x = const;
(2)y^2 + (-2⋅y0)⋅y + (-3x^2(x - x0)) = 0;
уникальное квадратное уравнение для каждого x?
Какая тебе математика, если ты гугл не освоил
Вот взять, допустим, x_random, пихнуть туда,
и найти для него y_random, затем провести прямую через точки: (x_random, y_random) и (x0, y0) - она ведь и будет касательной, и пройдёт также и через точку касания, так?
Угловой коэффициент при этом, равен угловому коэффициенту касательной, и может быть выражен через координаты этих двух точек.
(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)
- уравнение прямой, проходящей через две точки.
y - y1 = k × (x - x1) - уравнение пучка прямых, проходящих через точку касания.
k = (y2 - y1)/(x2 - x1) - угловой коэффициент из уравнения прямой, проходящей через две точки.
x1 = x_random, x2 = x0;
y1 = y_random, y2 = y0;
(или наоборот);
Ну, а затем, можно сказать, что угловой коэффициент равен угловому коэффициенту касательной, как-то вот так:
(y2 - y1)/(x2 - x1) = 3x^2/2y;
2y⋅(y2 - y1) = 3x^2⋅(x2 - x1);
y = 3x^2⋅(x2 - x1)/2⋅(y2 - y1);
А потом, зная что (x, y) - принадлежит кривой - перебрать их тупо на вычислительных кластерах.
И пошёл себе...
Ну правда же не могу найти.
>y = 3x^2⋅(x2 - x1)/2⋅(y2 - y1);
Или не, можно возвести всё это в квадрат, и приравняв с x^3 + 100 - найти x, решив уравнение 4-й степени. Решение Декарта — Эйлера, как-бы намекает.
Как виучить диффуры без задней мысли? Ответте очен надо(((((999999
Сколько будет корень кубический из числа:
1000001830870027297978298515729666505212884166162484148877922518975094790400970570522199072587355704878891442315545898076771516621174152673689989339035127902382837115000643507722347297620901638896364539973423858315699700262234535307858559283866203015657571681219536693250096025949031554596737416351572824833692221889257913680740633442898803535171147631300226004087420744628587268605510214842986268251087094778884059618606246138916115634757897366330021699409413593142129925945618521207896712941564970313323804632014769354909484054317079994590186747509687704251751159469797853131511220277941668575287968584246253996374974592963088856980532208103991683497889063594912128784355968752305284792294140570514319713024987124616127
У меня была слабая база в школе, а теперь я поступил на математический факультет. Более-менее справляюсь, но не покидает чувство что я не понимаю что-то из основ. Сейчас почитал про производные, и понял что я о них ничего по сути и не знал. У всех математических предметов которые мы изучаем Алгебра, Матан, Аналитическая геометрия есть связь, но у меня в голове совершенно нет полной картины происходящего, чувствую себя обезьянкой, которой дают формулы и она подставляет их на конкретные задачи. Что из вышего списка нужно почитать/послушать, чтобы хоть приблизиться к понимаю? Или ждать старших курсов, чтобы у меня всё это магическим образом само сложилось?
Списки для кого написаны?
Там очень уж много литературы. С чего начинать то?
А что конкретно тебя интересует? Распише подробнее.
*Распиши
Я хочу в полной мере понять смысл того что происходит в математике. Для меня маркером подобного понимания является возможность выводить нужные формулы самостоятельно, если забылись, или способность решать задачи альтернативными путями.
Я наверное немного наивно себе это все представляю? Если так, то просто посоветуй что-нибудь элементарное, чтобы я хотя бы пробелы закрыл которые есть.
Какая-нибудь книжка по теории множеств тебе зайдёт. Гугли рассказы о множествах и книжку Шеня.
Спасибо, посмотрю.
https://youtu.be/I5vSCY4-bR4?t=5m15s начал смотреть типа мультик для детей и тут пошли такие сравнения, что я тупо охуел. Это высшие абстракции для меня. Почему я такой тупой? Как это понять?
Я еще раз повторяю - та система даст в ответе все точки исходной кривой, проведя касательную к кривой в которой, она пройдет через заданную точку (x_0, y_0).
И направляя свою мысль к одному из своих старых ответов - мне похер всё равно как вы будете решать эту систему. всегда есть wolfram mathematica, ответ которой может (если повезет) навести на конструктивное решение
Возьмешь кривую попроще - получишь и систему попроще.
Все нужные аналитические действия я произвел, с меня-то какой спрос?
Проиграл с видео и твоей толстоты.
Знаешь, анон, тут такое...
Дана касательная. Определить координаты точки касания.
Гляжу сюда: http://kontromat.ru/?page_id=3599
Здесь - приравняли известное k с f'(x).
В результате, получили одно уравнение с одной неизвестной,
и решив его - нашли абсциссы точек касания в разных местах функции,
там, где прямая имеет этот же угловой коэффициент.
Это всё потому, что y = f(x); и y' = f'(x);
Но у меня же не y^1, а y^2 = x^3 + 100;
и k = 3x^2/2y; - уравнение с двумя неизвестными...
Если же выразить y через корень, с учётом того, что
>Когда решаешь уравнение вида x^2 = a, решение есть не только сам корень из правой части, а еще то же самое, но с минусом.
получится:
y = ±√(x^3 + 100);
y' = 3x^2/(2⋅±√(x^3 + 100)) = k;
И после всего, как-бы, вот:
9⋅x^4 - 4⋅k^2⋅x^3 - 400⋅k^2 = 0;
гет въебал
>В результате, получили одно уравнение с одной неизвестной
Про это я еще с самого начала тебе твердил
>Здесь - приравняли известное k с f'(x).
считаю, что только дебил не понимает геометрического смысла производной: "значение производной есть угловой коэф касательной, проведенной в этой точке"
>y = f(x); и y' = f'(x)
Нихера себе, такому нигде не учили же ведь.
Считаю этот косяк за составителями школьных учебников довольно критическим, потому что все тупые школьники не понимают обозначения y = f(x) = %выражение функции%
Отправляю к и сюда
Решай систему - получишь точки. Получишь точки - получишь касательные (если они вообще нужны).
А лучше иди штурмовать ангем с матаном, чтобы осознавать, что выражение y = f(x) не может задавать всевозможные кривые и логичней пользоваться выражением f(x,y) = 0 со всей вытекающей оттуда теорией.
Как развить навык мгновенного счета? Типа кинул взглядом и уже знаешь число.
>Нихера себе, такому нигде не учили же ведь.
Обозначать значение производной в точке буквой со штрихом?
Сап аноны, посоветуйте хороших учебников с теорией, формулами и задачники с практикой, за 8-9 и 10-11 класс.
в основном важны дроби, степени всех видов, корни, логарифмы, тригонтметрия ну и остальное тоже
в основном важны дроби, степени всех видов, корни, логарифмы, тригонтметрия ну и остальное тоже
Алимов 7-11 класс. За месяц, если будешь уделаять по часу в день, осилишь всё.
Учту, мне бы еще конкретно на логарифмы и тригонотметрию, тому что скоро зачет по ним.
Это в учебнике за 10 класс.
1000000610289636645809734072461876313339704
1949712060491086355761945489924035500130401
9502966954838708228926426599842777499156023
2310851236552408452866855041538248349726418
4572697078900319911336549388077443592117987
80565572293634528725674303
Проверить можешь тут: http://www.javascripter.net/math/calculators/100digitbigintcalculator.htm
Считал в столбик. Пикча отклеилась.
Ок, спасибо
Посоны, а уберите(?) по приколу чисто "Аноним" и день недели. Будут в итоге одни цифры. Это же /math/.
А текст - в hex-формате или двоичном виде, чтобы по хардкору.
число на 7 кончается
Никак. Самое главное - анализ данных. Данные - похуй какие имхо
а точнее - протестить способность анализировать пиздёж, например
Есть ли годные учебники которые не используют в школах, не люблю я просто наше школьное образование, с программой математики примерно с 5 по 11 класс?
> анализировать пиздеж
Всмысле понимать что тебе хочет или не хочет сказать человек в своей реплике?
Как просто понять эти все графики от функций? Вроде элементарно, но я туплю
Нарисуй графики и перенси руки человечков на них
Ой, тут, в твоём случае, разные индивиды могут определиться. Некоторые "слишком умные", которые будут тестировать на истинность то что ты написал, и другие - которые будут тестировать на истинность то что ты хотел донести. И кого к какой группе относить, лично я, не знаю. Но первые, определённо, бесят.
То есть. В разных областях знаний каждый может показать себя как гуманитарий и как технарь одновременно. Особенно это будет проявляться в неизвестной ему области.
я мимо из /ph/, не знаю зачем сюда зашёл
>которые не используют в школах, не люблю я просто наше школьное образование
Они довольно хардовые.
Колмогоров Геометрия
Пратусевич Алгебра и начала анализа
>я мимо из /ph/, не знаю зачем сюда зашёл
Что такое число?
Нечто состоящие из цифр. Цифру определим как символ, обозначающий количество удачных опознавательных актов восприятия.
Не люблю за то что темы довольно сжаты под учебную программу, хотелось бы что-то по обширнее и понятнее
>Нечто состоящие из цифр. Цифру определим как символ, обозначающий количество удачных опознавательных актов восприятия.
Что такое атк восприятия и опозновательный акт ещё что такое удача.
Учебная программа лишь маленькая часть из того, что там даётся. Серьёзно, зацени эти книги.
Можешь ещё почитать книгу:
За страницами учебника математики.
Восприятие - механизм, позволяющий воспринять информацию посредством сенсорного опыта.
Опознавательный акт - процесс, в ходе которого происходит отсеивание неупорядоченых данных, полученных во время акта восприятия, от упорядоченых. С игнорированием первых.
Упорядоченые данные - те данные, которые воспринимаются соответствующим предыдущим опытам распознания объектов
Неупорядоченные данные - те данные, которые опознаются восприятием как что-то хаотичное.
Удача - результат процесса, в ходе которого определяется воспринят объект как объект или не воспринят.
Неудача - результат процесса, где объект невоспринят, происходит возврат к первоначальному циклу восприятия.
>позволяющий воспринять
Сука, тафталогия, надо переписывать.
А жаль, у меня знакомый и так философ, а как покурит так вообще задвигает такое шо пездес
Посмотрел, но там программа 10-11 класса, мне бы начать так с программы 7-8 класса с 5 это я уже переборщил что-то, а потом по тихоньку и до этого доберусь.
И вообще я решил составить список годных учебников 7-11 класс и начать вести конспект с формулами теорией и практикой, чтобы все это выучить и не фейлить, потому что на парах мы работаем в темпе хард, никто ничего не успевает, а мне еще за прошлые годы надо подтянуть материал. я все правильно делаю? Или может посоветуешь какой альтернативный путь изучения, чтобы проникнуться и быстренько подучить все что проебал?
Бета-фикс
>Восприятие - механизм, позволяющий принять к обработке информацию посредством сенсорного опыта.
>
>Опознавательный акт - процесс, в ходе которого происходит отсеивание неупорядоченых данных, полученных во время акта восприятия, от упорядоченых. С формированием виртуальных моделей восприятия соответствующих, с определённой погрешностью в рамках %хуй_знает_каких% чему-то реальному(?) бля, запутался, сука
>
>Упорядоченые данные - те данные, которые воспринимаются соответствующими копии предыдущим опытам распознания объектов. Каждый опознанный объект определяется соответственно виртуальной модели.
>
>Неупорядоченные данные - те данные, которые опознаются восприятием как что-то хаотичное. Игнорируются восприятием.
>
>Удача - результат процесса проверки поступивших данных, в ходе которого определяется воспринят объект или не воспринят.
>Неудача - результат процесса, где объект не воспринят, происходит возврат к первоначальному циклу восприятия.
Я шизик и то знаю, что число это количественная мера.
Мера — философская категория, означающая единство качественной и количественной определённостей некоторого предмета. Согласно А. П. Огурцову, эта категория обобщает способы и результаты измерения предметов. Анализ меры исходит из важности интервала изменений количественных величин, в рамках которого можно говорить о сохранении качества предмета. Категория меры тесно связана с рядом философских понятий, в том числе относящихся к областям этики и эстетики.
Ну и что?
А может быть такое, что абстрактная африка тебе легко, а арифметика вообще не идет?
Это упрощенные модели восприятия графиков в декартовой системе координат.
Гугли графики парабола, кубическая парабола, синус, косинус, и т. д. - а потом глянь на рисунок.
Хуёвое определение. Не поддающееся моделированию или вычислимости(?). Его можно продолжать бесконечно.
Я спрошу - чем можно описать человеческое бытие, ты что-то ответишь, дальше чёто можно будет спросить и т д
Геометрию смотрел? Этот учебник больше не на детей, а на студентов, которые не изучали евклидовую геометрию в школе и хотят с ней ознакомиться.
>И вообще я решил составить список годных учебников 7-11 класс
По большому счёту, они все себя повторяют. То есть, в них одно и тоже, правда, в некоторых есть подробная запись, или дополнительные главы. Пратусевич - исключение, там, по сути, излагается матан за первый курс и Колмогоров тоже, это попытка осовременить геометрию.
Если с азов, то можешь читнуть Алимова. Не забудь решать задачи.
>я все правильно делаю? Или может посоветуешь какой альтернативный путь изучения, чтобы проникнуться и быстренько подучить все что проебал
Можешь у препода спросить книжки, лол. Просто в тех книгах, что я тебе советую гораздо больше, чем у тебя будут спрашивать, но прочтя их ты лучше будешь понимать матешу.
Ну я и так ща на первом курсе, на парах нас особо не спрашивают, мне надо для сессии и для себя, может в программирование пригодится
Мера – указатель на объективно существующую, фиксируемую аппаратурой единицу измерения являющейся точкой отсчёта в определённой системе.
не знаю нахуя составил
Всё что можно корректно описать, смоделировать - можно сэмулировать, а значит - автоматизировать.
Я так понимаю, процесс, как последовательность элементарных операций, ведущих от причины к следствию, т. е. от изначального состояния - к результату, можно алгоритмизировать.
А автоматизировать - можно управление этими процессами, т. е. их изменение.
Но так как управление - совокупность управленческих воздействий, как-бы придающих форму процессу, или процессам, само является процессом, также как процесс организации управленческих воздейстий - встаёт такой вопрос: возможно ли автоматизировать самоорганизацию процессов управления алгоритмизированными процессами так, чтобы исключить полностью синергетические процессы управления, порождающие в частности или в совокупности не автоматизированное управление.
>Но так как управление - совокупность управленческих воздействий, как-бы придающих форму процессу, или процессам, само является процессом, также как процесс организации управленческих воздейстий - встаёт такой вопрос: возможно ли автоматизировать самоорганизацию процессов управления алгоритмизированными процессами так, чтобы исключить полностью синергетические процессы управления, порождающие в частности или в совокупности не автоматизированное управление.
А кибернетики хуи пинают? Если оно может в классическое определение алгоритма и подпадает под стандартные вычисления машины Тьюринга, то можно.
Ну, епт, я же говорил, если алгоритмически разрешимо. А если нет, то и не нужно.
Взять например, бесконечный цикл.
Цикл пробегает проверяя значения, и если значения удовлетворяют условию - подается сигнал на исполняемый модуль, для исполнения набора элементарных операций и правильного осуществления управленческого воздействия, направленного на коррекцию этих значений, или среды, откуда они извлекаются.
По определению алгоритма:
Алгоритм — набор инструкций, описывающих порядок действий исполнителя для достижения некоторого результата.
Но здесь нет результата, это цикл.
>Всё что можно корректно описать, смоделировать - можно сэмулировать, а значит - автоматизировать.
Товар. Здание. Математическая модель.
Это можно корректно описать, смоделировать, и сэмулировать, но не автоматизировать.
Автоматизировать можно сам процесс производства товара, постройки здания, моделирования и настройки эмуляции модели, я правильно понимаю?
Как называется задача вида:
\int_0^inf f(x-c)dx=k, где k и c действительный числа?
Чё-то я не врубаюсь в координаты вектора.
Чем они отличаются от координат точек?
Почему их две?
насыпь спичек на стол. Спичка направлена туда, где ее голова. Возьми одну спичку, положи на центр стола. Теперь ты можешь выложить некое количество спичек (ломать можно) и указать любую точку на линии, которой она принадлежит. Теперь прислони еще одну спичку основанием к первой так, чтобы они не были параллельны. Теперь ты можешь выложить спичками по этим двум линиям любую точку на столе. Третья спичка даст тебе любую точку в комнате. Четвертая любую точку в твоей жизни, но ее еще поставить уметь надо. Числа векторов это количество спичек.
>Четвертая любую точку в твоей жизни
А теперь, автоматизировать бы организацию и превентивную доставку целесообразной информации об этом - прямо в нейроморфный нанобиочип по терабитовому каналу беспроводной связи.
>Нейроморфный
>Toshiba нашла способ создать такой вычислительный блок, который состоит всего из трёх логических вентилей и 1-битной памяти
Чё? 1 битовая? Это как? Меньше же двух нельзя? они поехавшие?
Блин, вы мне мозг поломали, я, конечно, загуглил, что оно транслируется в 2 бита всё равно, но что если допустить, что....?
Маняматики, никто не делает конспекты в электронном виде? Чем пользуетесь? (каким-нибудь . md с латех-расширением)
Что-то я заебался на бумаге писать, ибо пишу хуёво и на аккуратную запись какой-нибудь небольшой выжимки уходит куча времени.
Что-то я заебался на бумаге писать, ибо пишу хуёво и на аккуратную запись какой-нибудь небольшой выжимки уходит куча времени.
Знакомая одна херачила лекции по матану в ворде, потом заебалась осознала, что всё равно можно взять лекции у кого-нибудь, кто пишет аккуратно.
А так, если скорость печати позволяет, бери в зубы тех и пиши, там нет ничего сложного, и никто не запрещает херачить макросы набросок, который можно потом преобразовать в нормальную разметку. Но рисунки придется рисовать в тетради и потом оцифровывать в любом случае.
Но когда пишешь руками - запоминается лучше, моторика типа, поэтому либо учись свой же почерк разбирать, либо прописи попиши, поможет
Ну что же вы, алгебраны?
Я думаю тут есть те, кто ходил/ходит в нму, так вот какой статус будет иметь диплом на выходе, с ним можно идти в аспу или нужно официальное мат образование бакалавр+магистр/специалитет?
Кострикин-Манин, начиная с тензоров, если уже хоть немного знаком с линалом
Я тупой, поясните куда копать
Отбой, решил
В российскую аспирантуру, конечно, нет. В нормальную нужны рекомендации/публикация, которые поможет дать НМУ.
Понятно, спасибо.
Если станешь одним из 5-7 хардкорщиков, которые его оканчивают, то тебя с распростертыми руками заберут в почти любой крутой американский институт, и тут дело не сколько в дипломе, сколько в высочайшем математическом уровне, который эти выпускники имеют. Но для этого придется крайне много заниматься, фактически перманентно (~1.13 Grot)
>В российскую аспирантуру
В НМУ есть своя аспирантура, можно туда.
Логарифм неправильно нарисован.
5-7 человек - это жесть конечно, да я так попробовать хочу, просто интересно стало за перспективы.
>Grot
Что это такое?
>2 программы вербита (а также у него есть пост про геометрию есть и 2 поста про поп)
Как найти то, что в скобках?
цитата отсюда https://2ch.hk/math/res/106.html#1514
Возникает ли турбулентность при пердеже? Можно ли ввести управление чтобы не было звука? Есть ли исследования на эту тему?
В бэ как-то был тред о том, что нельзя нарисовать абсолютно новое животное, подобия которому не было в природе. А если взять неевклидову геометрию?
суп, матх.Ккак вычислить пикрел?
Клапан 150.37.064-3 плавного снижения давления, правый ( паровозик ), гусеничной коробки перемены передач, для трактора Т-150Г, Х Т З -181 производства завода ХТЗ.
Клапаны плавного снижения давления правого и левого бортов трактора типа Т-150
позволяют путем сброса давления на одном из бортов осуществлять плавные повороты трактора.
Можешь заюзать.
А вот для снижения турбулентности тебе может понадобится Alphacool Bubble Down G1/4 - Deep Black, что на втором пике.
Анончик есть ли какой-нибудь неебический способ избавления от корня?
к примеру V400=4V25, я вот только в уме могу подставить и решить, а нет ли какого нибудь алгоритма или чего-нибудь.
к примеру V400=4V25, я вот только в уме могу подставить и решить, а нет ли какого нибудь алгоритма или чего-нибудь.
> пишешь руками - запоминается лучше
Миф. Зависит от типа мышления.
Понял в чём фейл, название-то бит, а должен быть монит или унит. В любом случае особо ничего про них не гуглится, и это печально. Нарыть бы доказательство невозможности построения процев на монитах/унитах хуйня же вроде, там должно быть всё просто
Тогда можешь заюзать датчик давления с миостимулятором, работающим по принципу Super Abgymnic.
Для прочного контакта с мышцами можешь использовать электродные массивы.
Если уравнение, то пробросить корень в одну из частей, и возвести всё уравнение в квадрат. Очевидно, же.
Посоны, я застрял на теореме Виета и квадратных уравнениях. Какое-то говно собачье, магия. Ебут моск волшебными словами типа дискриминант, а не пояснят зачем это вообще нужно и как к этому дошли. Как это понять? Или это надо тупо зазубрить? Но чет не хорошо как-то тупо зубрить.
ax^2 + bx + c = 0
ax^2 + bx + c = 0 |/a
x^2 + (b/a)x + (c/a) = 0
x^2 + (b/a)x = -(c/a)
x^2 + (b/a)x = -(c/a) | + (b/2a)^2
x^2 + (b/a)x + (b/2a)^2 = -(c/a) + (b/2a)^2
(x + (b/2a))^2 = -(c/a) + (b^2/4a^2)
(x + (b/2a))^2 = -(4ac/4a^2) + (b^2/4a^2)
(x + (b/2a))^2 = (b^2/4a^2)-(4ac/4a^2)
(x + (b/2a))^2 = (b^2-4ac/4a^2)
(x + (b/2a))^2 = (b^2-4ac/4a^2)
x + b/2a = +- sqrt((b^2-4ac/4a^2))/2a
x = (- b +- sqrt((b^2-4ac/4a^2)))/2a
b^2-4ac - дискриминант.
Что касается теоремы Виета для квадратных уравнений - там система.
1 - приведённое квадратное уравнение. a = 1;
2 - уравнение вида ax^2 + bx + c = 0
Ты это просто зазубрил и знаешь, или как?
Что делать с высокой степенью математической тревоги? У меня от математики физическая боль.
Ну вот, в первом посте развёрнутый ответ в виде вывода x из ax^2 + bx + c = 0;
А теорему Виета - смотри тут:
https://ru.wikipedia.org/wiki/Формулы_Виета#.D0.9A.D0.B2.D0.B0.D0.B4.D1.80.D0.B0.D1.82.D0.BD.D0.BE.D0.B5_.D1.83.D1.80.D0.B0.D0.B2.D0.BD.D0.B5.D0.BD.D0.B8.D0.B5
Недавно такую срань решал, ты там первое слагаемое в числителе распиши через експоненту e^(1/x*ln(1+x)) и дальше дело пойдет в гору
Если не сможешь то утром могу покопаться в тетрадях и найти решение
Ефимов Н.В. - Высшая геометрия, - это такой крутой курс школьной программы?
Ребят, ищу помощи( с 8 по 14 включительно) буду благодарен
Что делал? Что не получилось? Какие вопросы?
Что-то не сходится, а где-то не вдупляю чего делать
сука, то мой пост был, думал наизичах найду, а хуй там - в закладках не было, короче вот:
"что нужно выучить по геометрии":
http://lj.rossia.org/users/tiphareth/1517171.html
"100 книг по математике":
здесь ссылки на 2 опроса
http://lj.rossia.org/users/tiphareth/1903372.html
комментарий к ним:
http://lj.rossia.org/users/tiphareth/1899211.html
Алсо, пока искал, наткнулся на обсуждение мемоса из архаического треда:
http://lj.rossia.org/users/tiphareth/1889881.html
ну и
http://lj.rossia.org/users/tiphareth/1555627.html
кст, в мемную комнату добавь Grot, а также линк на водовку-картофан
https://lj.rossia.org/users/tiphareth/1052017.html
больше ликбеза!
Планирую вкатываться в математику по книгам на английском. На данный момент есть знания за 8 класс. Какие подводные?
>http://lj.rossia.org/users/tiphareth/1555627.html
ПАЦАНЫ, Я СЕГОДНЯ ШЁЛ КОРОЧЕ ПО ГЗ И УВИДЕЛ ЗАЗНАЙКУ С
УЧЕБНИКОМ АЛГЕБРАИЧЕСКОЙ ГЕОМЕТРИИ, НУ Я ПОДСКОЧИЛ, РЕЗКО
ПЕРЕЕБАЛ ЕМУ В ЩЩИ С ВЕРТУШКИ И ПОЯСНИЛ ЕГО КРИКОМ "НЕ
ЛЮБЛЮ НОВОМОДНУЮ МАТЕМАТИКУ", потому что я угорел по
московской математической традиции, пацаны, дух ЛУЗИТАНИИ
живёт только на мехмате, где изучают функциональный
анализ, дифференциальные уравнения, где пацаны живут
интегралами, рядами Фурье и ебут теорию категорий в рот!
ЮНИТИ УЛЬТРАХАРДКОР КОЛМОГОРОВ-ФОМИН! Пацаны, ебашьте
абсрактных топологов, бурбакизаторов, жидоматематиков,
угорайте на лекциях, любите свой факультет, преподов и
московскую математическую школу! ГОВОРИТЕ ОТКРЫТО И СМЕЛО
ПРЯМО В ЛИЦО!
Это будет в шапке слудущего треда.
ты чо, лучше первокультурную версию тогда уж (оттуда же):
ПАЦАНЫ, Я СЕГОДНЯ ШЁЛ КОРОЧЕ ПО КОРИДОРУ ВЫШКИ И УВИДЕЛ ПАТЛАЧА В МАЙКЕ «МГУ», НУ Я ПОДСКОЧИЛ И ТРАНСВЕРСАЛЬНО ПЕРЕЕБАЛ ЕМУ В ЩЩИ С ВЕРТУШКИ И ПОЯСНИЛ ЕГО КРИКОМ «НЕ ЛЮБЛЮ ВТОРУЮ КУЛЬТУРУ», ПОТОМУ ЧТО Я УГОРЕЛ ПО (∞,1)-КАТЕГОРИЯМ, РЕБЯТА ДУХ ФУНКТОРИАЛЬНОЙ ТЕОРИИ ПОЛЯ ЖИВЕТ ТОЛЬКО В ПРОСТРАНСТВАХ, ГДЕ ЕБАШАТСЯ ПО ДИФФЕРЕНЦИАЛЬНЫМ ФОРМАМ, ГДЕ ПАЦАНЫ ЖИВУТ КОГОМОЛОГИЯМИ, ТОПОСАМИ ГРОТЕНДИКА И ЕБУТ КОМБИНАТОРИКУ В РОТ! ТОЛЬКО МОДУЛЯРНАЯ АЛГЕБРА ЯМАГАМИ, ТОЛЬКО МОНОИДАЛЬНЫЕ АБЕЛЕВЫ КАТЕГОРИИ! ЮНИТИ СУПЕРСИММЕТРИЯ 359! алгебраические геометры ебашьте общих топологов, компьютерсайнтистов, физиков, статистиков, угорайте на семинарах, любите свои доказательства, коллег и Школу! ГОВОРИТЕ ТОЧНО И ДОСТУПНО ПРЯМО В ЛИЦО! 359
>первокультурную версию тогда уж
Нет. Не нужна.
Вот и стандартный местный проблядок . Может, ты ещё и за интегралы топишь?
> Вот и стандартный местный проблядок . Может, ты ещё и за интегралы топишь?
Вот и стандартный местный проблядок . Может, ты ещё и за гамалогии топишь?
Конечно топлю. Я не второкультурная блядь.
Только вот я не местный.
>Может, ты ещё и за интегралы топишь
Конечно топлю. Я не пирвакультурная блядь.
Только вот я не местный.
Кстати, я тут подумал Вербит же говорил, что математику нужно изучать только для изучения теории струн. Получается, Вербит - второкультурщик?
другое дело, что ТС сама по себе есть абстрактная наука :) поэтому нет
Спасибо, хер бы я сам нашёл это в тифаретнике.
>Получается, Вербит - второкультурщик?
А чем его позиция принципиально отличается от позиции Арнольда? Он топит за полезную новую математику, "против" полезной для физиков старой. Его основной аргмуент против матанализа для математика изложенного в духе 1930-го года это то, что там нечего математику делать -- всё уже сделано (ну, насколько я понимаю его позицию).
Т.е. ему приписывают что он какой-то адовый сектант-первокультурщик, потому что он не особо подбирает слова, описывая мехмат, в то время как его позиция намного более здравая и сбалансированная. Он просто про это 1 раз, наверное, написал пост про геометрию и теорию струн, больше я не видел по крайней мере. Шифруется. Он ситх, тайный ученник Арнольда. Не назову его второкультурщиком, но всё не так просто.
Четвертый курс, методы математической физики. Онлайн калькулятор выдает решение интеграла с erf функцией, о которой я впервые слышу вообще. В общем, есть здесь кто-нибудь, кто может решить хотя бы подынтегральное выражение? Могу рублей 300 скинуть за решение, реально заебался с этим уравнением.
ок, ща попробую
Как развить пространственное мышление? У меня оно ниже среднего.
Попробуй порисовать кубы, или другие геометрические фигуры. Или можешь занятся 3d моделированием, созданием карт-модов для игр.
Спасибо, я тоже погуглил. Но мне нужно решение без этой функции
Не получится, она представляет неберущийся интеграл. Твой интеграл не берётся в элементарных функциях, но может быть с помощью неё быть вычислен.
На пике, как я понимаю, ошибка от автора? Ведь доказательство будет тривиальным.
Я только всякие матрицы-детерминанты-ранги знаю из линала (не ебу, что там ещё есть даже).
Из алгебры - определения групп, колец, полей и всё, кек. Ну какие-то теоремы-задачи ещё решал, но недалеко от определений ушёл.
Этого достаточно? Далеко от этого знания до тензоров?
И далеко от тензоров до внешней алгебры?
Анон, будь добр, проверь мое доказательство основной теоремы алгебры.
Можно ли вкатываться в математику по этим книгам?
https://openstax.org/subjects/math
https://openstax.org/subjects/math
>Планирую вкатываться в математику по книгам на английском.
>На данный момент есть знания за 8 класс.
Знаний пока мало. Ни капли фундаментальности еще нет.
Стоит знать теорию множеств да матлогику для начала, потом понять, что зарубежные об этом пишут, картину сопоставить. А потом, думаю, можно и вкатываться помаленьку.
>Какие подводные?
Будет сложно: дохера терминологии учить без аналогий в родном языке совсем тяжело.
Плюсом к тому будет факт, что там и пишут некоторые вещи иначе как-то слышал, что где-то забугром натуральные числа начинаются с 0 хотя ничего это не меняет. На самом деле у нас и своя математическая школа очень хороша, глянь только списка ОПа.
На этот пост наложен большущий хер закончившего матфаковца ИМХО. Несогласные идут нахер без обсуждений. Всем ня ^_^
Я имею в виду книги для нубов, уровня Precalculus. Думаю начать вкатывание отсюда
https://openstax.org/subjects/math
Гайз, на дваче на математику в последнее время спрос. Я знаю тут есть серьезные математики. Почему бы кому-нибудь не взять и не написать кратное и доступное даже дауну изложение, например, общей алгебры или действительного анализа? Какой-нибудь разумный начальный уровень знаний для тех, кто даже Винберга с Зоричем не осилил. Запилим учебник всем двачем!
Для тех, кто не осилил Зорича, уже есть Натанзон на 98 страницах. Хороших книг по алгебре я знаю не менее восьми, не вижу смысла писать еще один. Базовый материал где только не изложен.
Ага, а сотни вопросов в маттредах о том как вкатиться по-приколу постятся. И почему, интересно, хороших книг по алгебре только ты знаешь 8 штук? Почему никто до сих пор не написал одну самую понятную на все случаи жизни? Может потому, что особенности восприятия материала у всех различаются и чем больше разнообразие изложений, тем больше шанс, что каждый найдет для себя самое понятное?
на таком уровне в принципе не важно, какую литру читать, - все тупо и элементарно,
тобишь да, можно
но не вижу смысла в таком изощрении, на уркском же полно прекрасных книг
Посоны, поясните вот что, чому на дваче есть увлекающиеся математикой, если большинство тут живет в рф и математикой тут не заработать?
Посметьев проигровает с тебя, попивая мартини на своей яхте.
Ну, можно попробовать сразу в тензоры вкатиться. Но лучше пролистай весь учебник, там много чего полезного и интересного есть
Внешняя алгебра это и есть алгебра антисимметричных тензоров.
объясните пожалуйста, из чего следует неравенство на картинке
А че спрашивать, вкатывайся смело, если понимаешь, о чем речь в книжке.
Просто еще раз повторю — тебе всё равно придется тоже самое учить и на русском, если учишься в этой стране.
В итоге, профита просто не вижу, кроме лишних сложностей, обусловленных языковыми проблемами.
Но если ты пишешь из англоговорящей и там учишься сейчас, то наоборот, вариков больше нет кроме как вкатываться таким образом
Хз, тут спрашивать или в топологии
Поч f,g:C/{0} -> C/{0}, f: z->z^2, g: z->z^3
Не гомотопны? Грубо говоря, для любого z != 0 я могу соеденить z^2 и z^3 эквивалентно заданию пуи из I в R^2 соединяющий 2 зависимые точки (изменение радиуса и угла по времени t, всё дело естественно в полярных координатах) т.е. z^2 = А, z^3 = B;
A = (r^2, 2a), B = (r^3, 3a), тогда F(z,t) = Сt заданное: Сt = (r^2(1-t) + r^3t, 2a + at), тут конечно возникает проблемка того, что 2а и 3а могут перевалить за 2pi, но этого можно избежать заменив 2а и 3а на b и c соответственно, и тогда будет изменение угла b(1-t)+ct что и даёт нам гомотопию. Я точно чего-то не понимаю, или ошибаюсь в рассуждениях, но я немогу понять где.
Также не могу понять, почему окружность не стягиваема (нет, я конечно понимаю, почему непрерывной деформацией мы не можем привести её к точке, но я не понимаю этого из определения гомотопии, точно также как и с С\{0} мы можем построить путь который начинается в 0 и заканчивается в хt, тем самым мы сможем непрерывно каждую точку перенести путём в 0)
Сяп откликнувшемся анонам, я прост туповат, по этому такие проблемы.
Поч f,g:C/{0} -> C/{0}, f: z->z^2, g: z->z^3
Не гомотопны? Грубо говоря, для любого z != 0 я могу соеденить z^2 и z^3 эквивалентно заданию пуи из I в R^2 соединяющий 2 зависимые точки (изменение радиуса и угла по времени t, всё дело естественно в полярных координатах) т.е. z^2 = А, z^3 = B;
A = (r^2, 2a), B = (r^3, 3a), тогда F(z,t) = Сt заданное: Сt = (r^2(1-t) + r^3t, 2a + at), тут конечно возникает проблемка того, что 2а и 3а могут перевалить за 2pi, но этого можно избежать заменив 2а и 3а на b и c соответственно, и тогда будет изменение угла b(1-t)+ct что и даёт нам гомотопию. Я точно чего-то не понимаю, или ошибаюсь в рассуждениях, но я немогу понять где.
Также не могу понять, почему окружность не стягиваема (нет, я конечно понимаю, почему непрерывной деформацией мы не можем привести её к точке, но я не понимаю этого из определения гомотопии, точно также как и с С\{0} мы можем построить путь который начинается в 0 и заканчивается в хt, тем самым мы сможем непрерывно каждую точку перенести путём в 0)
Сяп откликнувшемся анонам, я прост туповат, по этому такие проблемы.
Математика универсальный язык же, при чем тут на русском учить или на английском?
Сама математика универсальна, но во-первых, есть "наречия" — система обозначений, принятых в одном или другом месте. Во-вторых, текстовое дополнение пишется на естественном языке, что порой затрудняет понимание.
Не видел ни одной книжки, написанной только на языке математики
Лучше в топологии продублируй.
Еще добавлю к словам анона выше, что стиль изложения на разных языках может быть разный. Хотя может тут больше от научной школы зависит, не знаю.
Господа, посоветуйте хороший справочник или сборник схем по всем разделам вышмата, чтобы оперативно вспоминать весь курс, а то у меня все разбросано в виде лекций, обрывков шпор, кучи пдф файлов и думаю не у одного меня такая проблема.
Хотя, тут скорее нет универсального рецепта и задача решается созданием собственного сборника материалов, настроенного под себя.
Хотя, тут скорее нет универсального рецепта и задача решается созданием собственного сборника материалов, настроенного под себя.
Внезапно, сборник Математика в техническом университете.
Ого, раньше не видел.
Базаришь?
Для нематематиков хорошо зайдёт. Базарю.
https://rutracker.org/forum/viewtopic.php?t=3026772
>справочник или сборник схем
мимо
>оперативно вспоминать
мимо
не говоря уже о качестве...
Алсо, вот еще тред вспомнился, как раз под твой вопрос https://2ch.hk/sci/res/382343.html
Щас еще свои бумажки открыл. Обфапался как конь уже, а еще только начало. Уже чесаться начал от мысли что в универе НЕДОДАЛИ.
Пожалуйста, помогите студенту разобраться с долгами
/un/
Вообще говоря, ОП-хуй в след трэде напиши про проги (любая с step-by-step'ом), а то здесь половина трэда - это тупое прорешивание устных примеров
>напиши про проги (любая с step-by-step'ом)
Ок. Только нужны ссылки. Сам не пользуюсь пошаговыми, проверяю ответ или считаю, чтобы его узнать.
Math, подскажите пожалуйста, что это за действие с двухсторонней стрелкой и цифрами -1?
О сложении одной строки/столбца с другой я в курсе, но что на пике обведено синим - я хз.
О сложении одной строки/столбца с другой я в курсе, но что на пике обведено синим - я хз.
Нестандартная терминология. Спроси в своей шараге, что это значит. Обычно такое не используется.
Я заочник, за 800 км от своей шараги, училки в интернете нет, не смогу спросить.
Анончик, пожалуйста, подскажи как этот определитель после двухсторонней стрелочки мог так измениться, какое действие можно было использовать?
Я прогуглил все свойства определителя, но не могу найти такого, чтобы можно было сопоставить.
>Анончик, пожалуйста, подскажи как этот определитель после двухсторонней стрелочки мог так измениться, какое действие можно было использовать?
В душе не ебу. Сказал же
>Нестандартная терминология.
такое не используется обычно.
>Я заочник, за 800 км от своей шараги, училки в интернете нет, не смогу спросить.
Спроси в группе шараги, у однокурсников, у группы факультета.
>Я прогуглил все свойства определителя, но не могу найти такого, чтобы можно было сопоставить.
Потому, что :
>Нестандартная терминология.
Понял, хорошо. Спасибо за ответ.
очевидно вторая строка расходится в три других с разными множтелями.
действительно, тонны нефти, спасибо!
>очевидно
Бля. Мне вот не было такое очевидно. Ты не любитель олимпиад случаем?
https://www.google.ru/search?ie=UTF-8&hl=ru&q=Step-by-step%20solution%20math%20programm&gws_rd=ssl
ТЫСЯЧИ ИХ!
https://yandex.ru/search/?text=%D0%BA%D0%B0%D0%BB%D1%8C%D0%BA%D1%83%D0%BB%D1%8F%D1%82%D0%BE%D1%80%20%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%BE%D0%B2%20%D0%BE%D0%BD%D0%BB%D0%B0%D0%B9%D0%BD%20%D1%81%20%D0%BF%D0%BE%D0%B4%D1%80%D0%BE%D0%B1%D0%BD%D1%8B%D0%BC%20%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5%D0%BC&lr=2
----->
https://www.kontrolnaya-rabota.ru/s/predel/funktsii/?function=2xsin(x)%2F(1+-+cos(x))&X=x&x0=0&choicer_off=1
(Один из примеров того школьника)
Как называются такие интегралы?
Не прикрепилось
Картофан, вторая культура.
А без мемов можно?
Сап, учоные великие, подскажите что дальше делать(
Я то сам решал, но говна нарешал
Я то сам решал, но говна нарешал
Кратный (там где n переменных)? Тройной (там где 3 переменных)?
криволинейный интегралы второго рода
Добра тебе
Помогите плс, пропустил несколько пар по матану
Где я обосрался?
Где я обосрался?
В другом ответе нихуя не видать, так что напишу.
Первый правильно взял, во втором обосрался
Там -2sin(2x)sin(sin^2 (x))
И не обсирайся больше
Да и не матан это. Так, десятый класс максимум производные-то брать.
Да и как это, ошибиться и не пойти самому ошибку найти, весь кайф от математики проебать пиздец
>Да и не матан это
эта школьная поебота называется калькулус, мимо твой кэп
Кто сможет помочь 15задание 1-4 номер?с меня любые кайфы
Почему линейная часть поверхности второго порядка при поворотах переходит в себя?
Сап, матач.
Есть один знакочередующийся ряд.
Нужно доказать, что сходится, причём доказать нужно хитровыебанно, а именно доказать по критерию Коши, что данная последовательность является фундаментальной, а значит сходится, доказать, что сходится ряд по признаку Лейбница я бы смог и сам, а тут затруднения возникли.
Нужна помощь.
1. 0 порядок стремления в знаменателе выше
2. Бесконечность беззнаковая разложи по корням и снова смотри про порядок стремления (снова в знаменателе выше)
3. 0, стремится снизу умножить-поделить на сопряженное
4. e^(0.6) второй замечательный. Сделай степень такую же, как второе слагаемое в скобках (не проеби равносильность выражения), потом предельным переходом получишь нужную степень
Не за что, иди проходи пределы заново, пока не поймешь, что они пиздец простые как же их решать.
О, любитель пределов! Ну-ка разъясни
И дополненную реальность в режиме реального времени туда пихнуть, с интернетом вещей.
Да хуйня. Эти в уме уже не посчитаю, но принцип очевиден. Когда не знаешь, что делать, надо раскладывать в ряды Тейлора до нужного члена в предельной точке. И снова глядеть про порядки стремления.
Как вариант — правило Лопиталя применить, но тут сложновато, согласен.
В твоём случае, так как в нуле, то хватит первого члена разложения в каждом отдельно взятом случае.
Давай сам только, вообще не до тебя сегодня, анон.
Господа, а что же тогда есть тру- матан?Анализ бесконечно малых?
бле, почему у нас все так хуево структурировано...
Что думаете о моей - http://i.imgur.com/KgenuM4h.jpg - программе? Семинары Бурбаки, ясное дело, читать статьи только по алгебраияеской геометрии.
Обращаюсь к вам в надежде на нормальный ответ.
Я изначально учился в математическом классе, но не на отлично, а средне, и после школы в вузе поступил на ин-яз. Вуз окончил 4 года назад, так что можете себе представить, как я помню математику. Неважно нахуя мне это нужно, но я бы хотел подтянуть свои знания хотя бы до уровня класса 10-11. Программу школьную помню в общих чертах, как без калькулятора считать не забыл, но в целом пробелов очень много.
Не могли бы вы мне посоветовать какое-нибудь универсальное пособие, которое помогло бы мне быстро освежить в памяти как решать различные уравнения и прочее? В интернете огромное множество книг, но когда начинаю читать, одни, например, не полные, другие имеют очень кратное объяснение решения (т.е. предполагается, что многое я и без этого помню) и т.д. Или мне начинать гуглить школьные учебники и просто перечитывать их и идти дальше?
Я изначально учился в математическом классе, но не на отлично, а средне, и после школы в вузе поступил на ин-яз. Вуз окончил 4 года назад, так что можете себе представить, как я помню математику. Неважно нахуя мне это нужно, но я бы хотел подтянуть свои знания хотя бы до уровня класса 10-11. Программу школьную помню в общих чертах, как без калькулятора считать не забыл, но в целом пробелов очень много.
Не могли бы вы мне посоветовать какое-нибудь универсальное пособие, которое помогло бы мне быстро освежить в памяти как решать различные уравнения и прочее? В интернете огромное множество книг, но когда начинаю читать, одни, например, не полные, другие имеют очень кратное объяснение решения (т.е. предполагается, что многое я и без этого помню) и т.д. Или мне начинать гуглить школьные учебники и просто перечитывать их и идти дальше?
На самом деле таки важно, нахуя тебе это нужно, потому что от этого зависит, что тебе следует читать. А так - универсальный ответ: наверни Сканави.
>На самом деле таки важно, нахуя тебе это нужно
Мне может подвернуться работа связанная с образовательным процессом, а ИМЕННО с школьной алгеброй и геометрией. Т.е. никакой высшей математики или какой-то узкоспециальной области. Это не моя специальность, но и не предполагается, что я должен быть как олимпиадник или буду преподавать это дело, я только должен понимать, что я вижу и как оно работает. Как мне сказали, могу купить тесты для подготовки к ЕГЭ или еще что-нибудь такое и попробовать их решить. Даже если я там не наберу максимум, но буду врубаться, что и к чему, все будет хорошо.
>Сканави
Вот сейчас нашел, вроде бы то, что нужно. Сразу же попутно спрошу совет, как мне заниматься? Писать конспекты, решать задачи и все?
бля, опять ты?)))))))))00000000000000000
За это время ты мог бы её на половину освоить,
деды на dxdy хоть и картошечные, но замечания правильные сделали, учиться по бурбакам не имеет смысла, с парочки книг, типа ТМ и Очерков, можно начинать, остальное только для закрепления
Ткачук Математику - Абитуриенту, параллельно почитывай, это идеально для освежения и структуризации школьной программы
>Ткачук Математику - Абитуриенту, параллельно почитывай, это идеально для освежения и структуризации школьной программы
Тогда спасибо, очень хорошо
>Писать конспекты, решать задачи и все?
Конспекты - трата времени, как по мне. Можешь выписывать формулы, но для этого я тоже не вижу смысла, если всегда можно посмотреть в книге. Тем более, это школьная математика, которую ты должен пройти максимально быстро. То есть, просто решай все задачи после каждого прочитанного раздела.
Кстати, когда будешь читать книгу, после каждой прочитанной теоремы пытайся доказать ее самостоятельно в уме, или хотя бы наметить стратегию доказательства, и только потом читай само доказательство, предоставленное автором. Если нет идей для доказательства, прочитай первые несколько строк доказательства автора и т.д.
>когда будешь читать книгу, после каждой прочитанной теоремы пытайся доказать ее самостоятельно в уме
Ой, с этим связанны болезненные воспоминания. Я когда то так в школе пробовал, когда плохо помнил параграф, но всегда за подобные вещи получал 2. Один раз даже доказал, но получил 3 потому что, как мне сказали слишком сложным и долгим путем пошел.
Можешь в английский? Попробуй это
https://www.amazon.com/Mathematical-Proofs-Transition-Advanced-Mathematics/dp/0321797094/
На либгене есть как сама книга, так и решебник (правда, решебник для предыдущего издания, неполный).
Может кто подскажет, что лучше почитать, чтобы освоить школьную программу для последующей успешной сдачи егэ(профиль) и дви по математике? Сканави? Нашел еще Туманова - Элементарная алгебра, вроде ничего. Заниматься буду один.
Пратусевичь, там но некторые разделы можешь там пропустить. Дальше есть книга по уравнениям с параметрами, название не понмю, найду скажу. По геометрии ещё что-нибудь там посмотри. А лучше прорешай дохуя вариантов.
Спасибо. Отпишись как вспомнишь, чекну тред к ночи.
Итак, так как тут пидорнули таполагов и туповатого модера, повторю свой вопрос, есть что книжки для начинающих про поля и кольца связанные понятия? Для начинающих, это значит без теории множеств, залезания в залупу чтобы доказать очевидное невероятное после небольших преобразований и подобного мусора который предназначен для тех кто хочет погрузится на самое дно.
Ну да, лучше же вызубрить доказательство из учебника, нихуя не понимая притом, и получить 5.
Школа такая школа.
>Для начинающих, это значит без теории множеств
Нету. Даун, кольцо определяется через множества, как и прочие алгебраические понятия вроде группы или поля.
Поясню более подробно что я хочу.
Вот в вышмате если выучить теорию бесконечно малых/больших и действия с ними куча сложных доказательств, которые нужны при изучении интегралов при помощи пределов коши или кто там был волшебным образом становятся по настоящему очевидными, без небольших преобразований, из самой сути действий над бесконечно малыми/большими.
Я ожидаю получить точно такое же но только в пределах общей математики. Я не про подведения основы под ассоциативность/дистрибутивность в духе бурбакистов.
>Кольцо (также ассоциативное кольцо) в общей алгебре — алгебраическая структура, в которой определены операция обратимого сложения и операция умножения, по свойствам похожие на соответствующие операции над числами.
>АБИЗАТЕЛЬНА ЧЕРЕЗ МНОЖЕСТВА НУЖНА
>настоящему очевидными, без небольших преобразований, из самой сути действий над бесконечно малыми/большими.
После изучения множеств тоже всё будет по настоящему очевидно.
Хотя, можешь сразу категории ебать.
Определи ка мне число один через теории множеств.
>Определи ка мне число один через теории множеств.
{Ø}
Может прекратишь этот цирк про илитарность множеств и их богоизбранность и начнешь советовать книжки?
Винберг, Кострикин.
Ну ещё Бурбаки. Лучше с них и начни.
Надеюсь в аду у тебя будет свой личный котел, рядом с группой бурбакистов.
Блядь, как же меня бесит этот тупой сучий потрох, эту гниду с картинкой нигера я встречаю уже который раз, и все время она несет какую-то хуйню и ведет себя неадекватно. Собственно, на парашу пидора
мимо алтфак
Это разные люди, картинка популярная просто. А так меня она тоже бесят, лучше бы ебальник математика приклепил.
Как же бесят эти полтора уебка которые из треда в тред носят это говно. Один жрет картофан и орет как вкусно, второй мастурбирует кольцом вычета пока никто не видит
Аршинов, Садовский "Грани алгебры", "Коды и математика". Любые книги по основам теории чисел, например Михелович. Постников "Алгебраические числа и теорема Ферма". В конце первого тома Бурбаки Коммутативная алгебра есть исторический обзор, не лишним будет почитать.
Заодно список основных книг по алгебре:
Для выборного чтения: Rotman, Knapp особенно вторая часть, Aluffi
Для чтения подряд: Isaacs, Rowen, Lorenz, Onishchik-Sulanke
Название у всех этих книг одинаковое, "Algebra"
Безнадежно устаревшее: Ленг, Hungerford, Маклейн-Биркгоф, Ван-дер-Варден
Изначально бесполезное: M Artin, J Gallian, Dummit-Foote, Axler, Винберг с Кострикиным
Еще есть книги Грийе (Grillet), Weintraub'а и Adkins'а, Городенцева. Они менее стандартны в плане изложения, но может именно это тебе понравится.
Для выборного чтения: Rotman, Knapp особенно вторая часть, Aluffi
Для чтения подряд: Isaacs, Rowen, Lorenz, Onishchik-Sulanke
Название у всех этих книг одинаковое, "Algebra"
Безнадежно устаревшее: Ленг, Hungerford, Маклейн-Биркгоф, Ван-дер-Варден
Изначально бесполезное: M Artin, J Gallian, Dummit-Foote, Axler, Винберг с Кострикиным
Еще есть книги Грийе (Grillet), Weintraub'а и Adkins'а, Городенцева. Они менее стандартны в плане изложения, но может именно это тебе понравится.
Хоть бы аннотации какие написал для каждой книжки, а то малополезный список.
Ротман – задуман как замена Вардену и Маклейну, обширный материал, можно использовать как справочник по отдельным главам.
Кнэпп – то же самое, плюс база по алгебраической геометрии, есть схемы.
Алуффи – все с теоретико-категорной точки зрения, но гомологической алгебры нет.
Айзекс – приводятся подробные доказательства всех утверждений, но некоторые темы игнорируются, например нет тензорного произведения. Роуэн – похожая ситуация. Как и у Айзекса, изложение близко к элементарному, оба избегают категорий, пока это целесообразно. Модуль определяется раньше кольца.
Артин – плохая книга от неплохого математика, подразумевается крайне доступное изложение как у Винберга, но в итоге материала очень мало, большинство нужных вещей там не найти, в итоге книга просто бесполезна.
Винберг – хорош только последними главами про группы Ли и теорию представлений. Модули определяет в девятой главе.
А про Зуланке-Онищик чего скажешь? Это ж вообще чуть ли не популярная литература.
Э, а Городенцев куда делся? Топчик же
Первый том если только популярный.
Больше геометрического флейвора, что нравится не всем.
А как же Кострикин-Манин? Тензоры же топово рассказываются
Отучился давно в универе, и уже совсем не помню, как брать производные таких сложных выражений, оче надо помочь хорошему знакомому. Если тебе несложно, анончик, то выложи ход решения. Лично у меня вышло y' = 1/(1-e^x), но я не уверен.
> Безнадежно устаревшее: ... Маклейн-Биркгоф, ...
А что такого поменялось, что они устарели?
вопрос по функциональному анализу:
вот есть отображение Fx из пространства ограниченных последовательностей l_2 в пространство ограниченных последовательностей l_1, но мне не понятно, что это означает. Объясните пожалуйста, это является серией отображений? Почему на первом месте в этой последовательности находится 0? Во втором элементе последовательности есть x^2(1), это означает что первый элемент последовательности возводится в квадрат?
Решетки (lattice) более нн актуальны, кажется.
Школьник ИТТ. 10 класс, пошел на районную олимпиаду. Сам не смог адекватно решить, в интернете не нашел.
В 1 задании написал x^4095+x^4094+...+x+1
Во 2 задании написал, что sqrt2 примерно равен 1.4 и с таким расположением точки E окружность не может пересекать ту точку, которая сделала бы треугольник ABF равнобедренным.
В 3 задании подобрал все возможные варианты переключения маяков около того маяка, который был выключен пока остальные все были включены. В итоге аыяснил, что никак нельзя погасить всё одновременно.
Есть шансы?
В 1 задании написал x^4095+x^4094+...+x+1
Во 2 задании написал, что sqrt2 примерно равен 1.4 и с таким расположением точки E окружность не может пересекать ту точку, которая сделала бы треугольник ABF равнобедренным.
В 3 задании подобрал все возможные варианты переключения маяков около того маяка, который был выключен пока остальные все были включены. В итоге аыяснил, что никак нельзя погасить всё одновременно.
Есть шансы?
Каким образом можно удобно раскрыть (1+x+x^2+x^3..+x^10)^2 ? Вроде бы понятно что тут будто интервалы перемножаешь, ну то есть минимум при переумножении будет 1 и максимум x^20, значит без кэфов получиться 1+x+x^2...+x^20 , но как кэфы вычислить?
>А что такого поменялось, что они устарели?
У них две книги: Survey of Modern Algebra - этакое введение уровнем попроще и просто Algebra - очень плотная (в смысле стилистики) книга уровнем повыше, третье издание которой выходило в 99-ом. Думаю, он имел в виду первую книгу, первое издание которой вышло в 41-ом.
ну помогите же, неужели никто не знает функциональный анализ?
Господа, расскажите кратко, если будет время, свой алгоритм обучения и познания математики и актуализации банка знаний?
У меня почему-то получается так, что я ныраю из одной области в другую, и не могу увидеть границ.
У меня почему-то получается так, что я ныраю из одной области в другую, и не могу увидеть границ.
Математика мертва и денег на ней не заработать, иди в программирование
Не согласен с тобой, скорее.
Математика - один из самых богатых и старых языков описания мира, процессов. Для понимания многих прикладных дисциплин и для общего развития, я считаю, математика - это просто маст хэв, а лично для меня это еще и приятное хобби, отдушина.
Чаю. У меня знакомый преподаватель по математике, красный диплом, все такое, так тот бугуртит регулярно с одного знакомого, который в 8 раз больше зарабатывает и занимается программированием.
Рисовать пробовал? Вот для души вообще заебись рисование заходит.
По теме: какие у тебя знания уже есть? Calculus спивака осилить можешь?
>денег на ней не заработать
Да кому они нахуй нужны? Нужны деньги - пиздуй в /biz/
Я тоже так думал, пока наконец не осознал что без денег от мамки не сьехать.
(1...x^10)x(1..x^10) = (1..x^10)x1+(1..x^10)x+...+(1..x^10)x^10 = 1 + 2x + ... + 2x^19+x^20
А как без полного раскрытия скобок узнать коэффициенты?
первое верно, второе нет (если я правильно понял чертеж), третье расскажи какие варианты пробовал и почему это все возможные.
пока не пробовал. сейчас обмазываюсь мат логикой и теорией полей
у нас есть 10 слагаемых. В каждом из них одночлен какой-то степени может получить только +1 коэффициент. Но с какой-то скобки он перестанет их получать.
Я прочитал калькулус тотомаса.
Но всего я егг не понял. Возникли проблемы в полярных координтах и векторах из за языка. Ну и ряды что то я совсем не понял.
Есть что то другое по этой теме?
И сколько и что мне еще нужно читать чтобы понимать физику ландау лившица?
Но всего я егг не понял. Возникли проблемы в полярных координтах и векторах из за языка. Ну и ряды что то я совсем не понял.
Есть что то другое по этой теме?
И сколько и что мне еще нужно читать чтобы понимать физику ландау лившица?
Почему техмакер нихуя не делает, когда я нажимаю на сборку?
При этом если из командной строки компилирую, то всё работает.
При этом если из командной строки компилирую, то всё работает.
Курс теоретической физики Л-Л рассчитан на людей с выраженной склонностью к математике и развитой интуицией. Если тебе даже в калькулюсе что-то непонятным осталось, то Л-Л тебе не освоить никогда. Точно также, как не все люди могут стать выдающимися художниками, например. Попробуй курс попроще, лекции на ютьюбе поищи.
Тогда гораздо пизже бы с ней жить было.
Не хотел бы уезжать же.
могут, но какой ценой...
Как сделать b и c?
1 + aa + a + aaa =
1 + aa + a(1+ aa) =
(1 + a)(1 + aa)
Ну b понятно еще, а вот с (c) вообще не могу управиться.
группируй а куб а квадрат, а в четвертой а в пятой и т д. Затем выноси общий множитель за скобки
Хуй знает, у меня получилось (1+a^5+a^10)*(1+a+a^2+a^3+a^4)
ни математика ни программирование здесь не причем.
препод просто не хочет денег
Как не хочет то, он же бугуртит с программиста насчет денег.
>он же бугуртит с программиста насчет денег
если это все, что он сделал, мне жаль.
Вопрос, возможно, и глупый, но всё-таки: как доказывается то, что в любой группе ( и некомутативной тоже) порядок элемента ab равен порядку элемента ba?
В алгебре молчат, тут ещё запощу.
В алгебре молчат, тут ещё запощу.
пусть (ab)^n = e, тогда ba(ba)^n=bea=ba
Бля, это же очевидно. Спасибо, выручил.
Что ты несешь? По твоему тут кто угодно может ящик без задней мысли скрутить?
И при чем тут выдающесть? Карл саган по твоему был йоба математиком?
Ну и напоследок, я не понял из за инглиша много чего.
Дмитрий Анатолиевич, мы знаем, что вы скажите. Надо помимо основной работы заниматься туевой хучей вещей и абсолютни забить на личную жизнь. А можно было не быть таким лошком, а ПРОСТО пить в подъездах с другом Вовой, как вы и придти к успеху. Хули остальные так не сделали, вот дебилы бля, правда?
>не все люди могут стать выдающимися художниками
хуевый, однако, пример,
вспомни, что ты живешь в 21-ом веке :(
Как привести матрицу к диагональному виду?
Вот нахожу собственные числа,обнуляю числа вне диагонали, и тупо вместо Альфы вставляю?
Вот нахожу собственные числа,обнуляю числа вне диагонали, и тупо вместо Альфы вставляю?
>тут кто угодно может ящик без задней мысли скрутить?
Чего?
>И при чем тут выдающесть? Карл саган по твоему был йоба математиком?
"Выдающесть" здесь при том, что что курс Л-Л написан выдающимися физиками для выдающихся физиков, а уж точно не для тех, у кого проблемы с калькулюсом. Зато при чем тут Карл Саган непонятно уже мне.
>я не понял из за инглиша много чего.
Типичное оправдание. Уж не знаю насколько это правда, но о твоем интеллектуальном уровне свидетельствует уже хотя бы тот факт, что для изучения предметы ты выбрал книгу на плохо знакомом тебе языке.
Ах да, "по-твоему" пишется через дефис.
>вспомни, что ты живешь в 21-ом веке :(
В чем, собственно, проблема? В двадцать первом веке перевелись художники? Почему в конце грустный смайлик?
Посоны, вопрос от нематематика. Поясните, есть ли термины обозначающие внутреннюю поверхность какой-то %хуйни_нейм% и внешнюю поверхность. Если есть - то какие. И как вообще определяется внутренняя поверхность или внешняя.
Я надеюсь на на грани того "эту часть примем за внутрненнюю, эту за внешнюю, потому что нам так удобнее"
суп котаны, не совсем по теме но интересно к чему бы вы больше отнесли математику к физике или к метафизике (в соответствующих пониманиях)
>ландаулившиц самие знаменитие физеки от физеков для физеков ат души душевно в душу
>язека ти не знаишь вот и не панимаишь
А по существу есть что сказать? Или цепляться к ошибкам это верх математической мысли?
Не знаю, выглядит как хуйня на этом вот уровне
>надеюсь на на грани того "эту часть примем за внутрненнюю, эту за внешнюю, потому что нам так удобнее"
Т.к у нас не только 2D 3D, но и хуй знает сколько D. А после того что вообразить затруднительно могут быть пространства где хуй поймёшь что там снаружи а что внутри.
Нет, я в принципе не против если для 2D и 3D оно верно, но мне хотелось да, я еблан, не написал об этом чего-то универсального.
Размерность тут вообще не причём.
>Внутренность — объединение всех открытых множеств
Короче у окружности нет внутренности, так? С кругом то всё понятно.
Да.
Посоны, ещё один тупой вопрос от нематематика, если у нас есть некое (X Demensions) 2D пространство и 3D пространство, из 3D можно сделать проекцию в 2D пространство. Можно ли сделать проекцию из любого X D рандомного пространства с Х > 3 в пространство 2D и 3D ?
Ты очень толстый.
Да. Распиаренный тессеракт как раз и является проекцией 4д куба в 2д/3д пространства.
Чому Клён не считает сумму ряда? ЧЯДНТ?
Уже разобрался.
Ок, тессеракт является, Вас понял. Но именно по существу задачи ответа не увидел.
Алсо
> not perfect representation but it as close as we can get
Хотя, если подумать, любая проеция всегда упрощение. Передача данных только с одной точки зрения, не дающей картины в целом, а значит является полнейшей хуйнёй.
Возможно меня не интересует не проекция. Но люди на другое, наверное, не способны
Ну и да, наверное последний вопрос, если у нас X Dimensions, обычно, равно целому числу, оно может быть равно 1/2 например?
Да. Гугли фрактальную размерность.
И это "по существу"?
>Математический анализ. 1 топ Зорич.
Хули все эти учебники такие непонятные. Дайте нормальную книгу где каждая запись дублируется человеческим языком. Я ебал разгадывать эти ребусы.
>пик
Хули тут очевидного? как это вообще прочитать? Может кому не впадлу и он покажет мне как из знаний материала книги который был до этой строчки. (3 страницы, лол, мда) я должен оказаться способен прочесть это. Каждый раз когда я от нехуй делать пытаюсь посмотреть математику, то обнаруживаю, что через 20-30 страниц от начала я уже нихуя не понимаю, что написано и никак не могу понять обращаясь к взятому мной учебнику..... Не то как одно из другого выводится, а именно что же тут блять написано.
книга
http://www.alleng.ru/d/math/math460.htm
читаю теорвер, а с ней и комбинаторику Феллера.
Помогите дауну:
В примере про размещение 3 различных шаров в 3 коробки выходит 27 комбинаций, то есть 3^3=27, есть рисунок-отображение комбинаций. Все ок. А если типа будет 4 коробки, то будет 3^4 = 81 и т.д.
Тут мне присралось просто немного изменить условия, пускай будет 2 различных шара. Ну и отобразить это. Блядь, у меня получилось 9 ебаных комбинаций:
{ab| | } { |ab | } { | |ab }
{a |b | } {b|a| }
{a | |b } {b| |a}
{ | a|b} { |b|a}
Где даун совершил ошибку?
Помогите дауну:
В примере про размещение 3 различных шаров в 3 коробки выходит 27 комбинаций, то есть 3^3=27, есть рисунок-отображение комбинаций. Все ок. А если типа будет 4 коробки, то будет 3^4 = 81 и т.д.
Тут мне присралось просто немного изменить условия, пускай будет 2 различных шара. Ну и отобразить это. Блядь, у меня получилось 9 ебаных комбинаций:
{ab| | } { |ab | } { | |ab }
{a |b | } {b|a| }
{a | |b } {b| |a}
{ | a|b} { |b|a}
Где даун совершил ошибку?
Формула %количество коробок%^%количество шаров%, а не наоборот.
Обращайся
Если невозможно заиметь полную и не противоречивую аксиоматику, то нахуя вообще анус рвать с доказательствами хуиты которая в любой момент может оказаться говном говна?
Поищи книги по доказательствам и элементарной теории множеств (Velleman "How to Prove It: A Structured Approach" например, первые главы элементарных книжек по любой теме, из известных мне: Munkres "Topology").
По анализу можешь взять простой учебник для ПТУшников: Зельдович "Высшая математика для начинающих физиков и техников". Так же великолепный элементарный курс калькулюся для нубов на курсере: https://www.coursera.org/learn/single-variable-calculus
>Поищи книги по доказательствам и элементарной теории множеств
Там объяснят базовую нотацию.
Да, но почему??? Ведь до этого умножали именно на количество коробок
Вообще, неплохо бы добавить вот это в шапку большими буквами и поближе к началу. По (пре-)калькулюсу, кстати, на курсере еще аж два курса есть, для совсем начинающих.
Как научиться геометрии и словно Боженька проворачивать фигуры в уме и строить их? У меня пространственное мышление ниже среднего. Мне даже тяжело понять, что близко, а что далеко, хотя у меня и близорукость. Как стать знатоком геометрии? Как наверстать то, чему меня не учили от 1 года?
Это не геометрия, а архаичная муть. Геометрию Евклида упразднил Лобачевский в 19-м веке.
Современный подход к геометрии - это изучение объектов, представимых локально окольцованными топосами. Ничего там "представлять" и не надо. Картинки рисуют художники, а не геометры.
Как я без понимания такой базы буду топосы мучать?
Как сделать дабы тупо смотришь на формулу и как-бы пробежал мультик, где веселые циферки связываются за ручки, одна отрезает другой бензопилой часть и это типа дробь и тд
Мне кажется моя проблема в том, что у меня клиповое мышление. Как это побороть? Как захотеть читать книжки без картинок?
Посоветуйте книжку, которая бы охватывала весь уровень младших классов.
Можно ли извлекать фан от математики? Я просто хз даже как к этому говну подлезть. Чтобы выучить ЯП можно какие-нибудь говноигры делать. Чтобы выучить язык можно худлит читать. Чтобы в ТОЭ шарить можно схемки паять.А здесь все веселье исключительно от решенной задачки?
Можешь выёбыватся на дваче знанием теории категорий и модулей.
Какого из НМУшных лекторов алгебры и геометрии можно послушать с наибольшей пользой для себя, учитывая свой околонулевой уровень знаний? Естественно, предполагается параллельное чтение учебников с решением задачек.
Можно. Достаточно любить узнавать что-то новое.
Можно. Достаточно любить узнавать что-то новое.
Придумывать интересные задачки, играться с числами, применять матан в электронике, алгоритмах, криптографии, астраномии, машинном обучении.
двачик,помоги мне пожалуйста
Страшно, котаны. У меня от этих уравнений уже повысилось сердцебиение.
1. решить систему 5 уравгнений отн. 7 неизвестных. соотвктственно, будет 2 параметра - координаты точек на плоскости.
2. приравнять точку одной плоскости точке другой и посмотреть что получится
3. а) yi=xi и порешать б) подставить образ в аффинное и посмотреть
а можно по-подробней,я просто проебывал геометрию
Есть система дифференциальных уравнений от 3 переменных x1,x2 и t, попытка проинтегрировать которую методом Рунге-Кутты не выходит из-за возникающего переполнения. Можно ли доказать, что с этой системой что-то не так? И еще, в процессе отладки я обнаружил, что при увеличении t x1 остается относительно неподвижной, а х2 уходит в минус бесконечность.
У меня уже голова кипит, чему в 3а равен x:16, 4 или +-2?
>-2 не имеет смысла
чет проиграл
Подставь в уравнение и узнаешь.
Это же троллинг?
Нет, школьник 7-классник.
sqrt(x)-4=0
sqrt(x)-4+4=0+4
sqrt(x)+(4-4)=4
sqrt(x)=4
нетрудно доказать лемму:
x=y <-> xx=yy
(sqrt(x)sqrt(x))=44
дальше надо доказать, что произведение квадратный корней равно x и дело в шляпе...
Это друга. Как по мне, в этом уравнении x=16.
P.S.И нет, не 7 класс, а 8(хотя разницы почти никакой)
Можно по понятней(на уровне средней школы)?
Что такое ИВ?
Что такое явная скалярная функция ортогонального ряда, и как рассчитать частичные суммы?
>невозможно заиметь полную и не противоречивую аксиоматику,
Нихуя не понял.
Правелно множыства и прочийа оксиоматика прастое верунство толька конструктивная матемотика нипративаричива. Гилберта надо довно изгнать с его фармолизмам! Толька Хотт, толька уневалинтные аснавания математики!!! Брауэру слава!
Брауэер даказал что матиматика в ZCF ниправтиваричива ясно ок? Там ещё был Годель со сваей тиоремой о ниполноте любой фармальной сестемы.
Еще был Альфред Тарский, который доказал теорему о том, что если нумералы Гёделя заменить на действительные числа, то теоремы о неполноте не выполняются. И его ученица Робинсон, которая доказала, что если заменить на рациональные, то снова выполняются.
И тут я начал понимать, что мой уровень математики где-то на середнячок в 3 классе. Может посоветуете книжки для таких олигофренов? Или просто брать школьные и решать на бумажке до просветления?
>Может посоветуете книжки для таких олигофренов?
Бурбаки.
>Или просто брать школьные и решать на бумажке до просветления?
Да. Так и делай.
Вставь пропущенные цифры: 4 + 2*5 = 601. Найди сумму всех пропущенных цифр.
я даже это не могу, блеять
Даже с разметкой попутал.
Спасибо
Я же толстил с Бурбакоми. Лучше наверни Курант Что такое математика.
Арбуз весит 4 кг и ещё половину своего веса. Сколько весит арбуз?
Почему арбуз весит 8 кг? Он же должен весить 6, нет?
Почему арбуз весит 8 кг? Он же должен весить 6, нет?
Да я пытался. Но я тебе говорю, что у меня с 4 классом проблемы даже.
Тогда бери учебник за 4 класс и читай его.
w - вес арбуза.
w=4+w/2
w/2=4
w=8
Но может еще что-то посоветуешь вообще для дошкольников? Может мне когда-то чего-то недоказали, что всем очевидно?
Почему для меня это выглядит словно наперстки и попытка обмануть?
http://metaschool.ru/pub/test/index.php?testId=17
4 класс. Курс математики начальной школы
Вы набрали 25 баллов из 30.
[fail]
Надо еще потренироваться, чтобы набрать хотя бы 27 баллов.
А чтобы оставить свое имя в таблице результатов, нужно успешно сдать тест после входа в МетаШколу с паролем
И это при том, что я использовал калькулятор. Какой же я дебил.
Читай учебники с 1-го класса. Если что-то знаешь, что быстро прочитаешь. И так до 11.
Задача с арбузом подъёбка для школьников. И большинство людей её решать неправльно.
Посоны, а может у меня дискалькуляция? Что делать с ней?
Справка от врачей есть? Или это маня-само-диагностика?
Конечно же второе.
Тогда скорее всего у тебя её нет.
Но меня серьезно плющит даже от арифметики и сравнения чисел.
Пока нет справки от врачей нельзя говорить о диагнозе. Может ты ипохондрик?
Да, я ипохондрик. Даже сказал бы киберхондрик. В моем списке стоит от рака мозга до шизофрении. Но теперь я решил, что я вообще истероид с пограничным состоянием психики. Но как мне достичь хоть каких-то возможностей в обучении математике? Мне сложно сосредоточиться.
Начинай с простых задачек. Решай математику с самого первого класса. Не будет тревоги, сможешь сосредоточиться.
Да я вот только что начал. Там задание вроде посчитай сколько домиков и назови цвет самого высокого. Я не знаю название такого цвета и у меня начинается паника.
Скрин?
Выбрал совсем случайный учебник.
А на русском нет? Для меня это звучит, как шизофазия. Ну или переведи мне.
Да говорю, что совсем случайный выбрал.
Сколько этажей в каждом доме? Какого цвета самый высокий дом? Какого - самый низкий? А
дома одинаковой высоты? Составь еще вопросы
о домах со словом "сколько"?
Лол.
>Сколько этажей в каждом доме?
1 - 9
2 - 6
3 - 6
4 - 3
Ты смог это сделать?
>Какого цвета самый высокий дом?
Здесь косяк самих авторов учебников. Можно назвать цвет светло-коричневым.
>А дома одинаковой высоты?
Светло желтый и персиковый.
>Составь еще вопросы
Почему авторы не могли нормально покрасить дом и сколько же сил они вгрохали на такую ебанутуй задачу?
Всё.
Я пытался посчитать, но сорвался, ибо надоело.
Я выбрал случайный учебник, может попробуешь поискать за меня в гугле?
Лучше возьми решебников, там можно ответы проверить же.
Самый высокий - бежевого. Самый низкий - ээ, тоже бежевого?
Походу украинские учебники для младшей школы слишком сложны для русского взрослого мужика. Ох уж эти киберхохлы.
в средней школе не рассказывают про действительные числа? Вкратце: действительные числа это единственное непрерывное упорядоченное поле с точностью до изоморфизма. Доказательство единственности и существования малоинтересно, не буду его приводить. Главное, что можно применять аксиомы поля и делать из них выводы, соответствующие алгебраическим преобразованиям. Единственная сложность в определении корня: корень это решение уравнение x^2=a, т.е. такое и только такое число x, которое при умножение на себя дает a.
хуёлсто. Реши то же уравнение в Z/nZ раз такой нестрогий.
Аноны, WTF? Область сходимости [-1;1] получается, уже пару раз прорешал. Схуяли тут такой ответ? Вроде как правильный.
Может кто подсказать, как найти распространение электро-магнитных волн в волноводе, если при Z=0 у нас есть Ez (r, fi, tetta)
Сап, математикам и прочим цифроблядям, хелпаните с данным тестом, могу кинуть в текстовом варианте. В вкантактель можете кинуть ответ, заранее спасибо, добро двач!
Ссылка на Вкантактель:vk.com/id394715992
Ссылка на Вкантактель:vk.com/id394715992
Меня всё чаще посещает ощущение, что вопросы тут постят студенты с проблемами, а ответы - школьники.
This. Только школьники-математики, разбирающиеся лучше большинства студентов. Хотя в тредах в сци бывали потрясания импакт-факторами журналов со своими статьями.
Сап, аноны.
>Подсчет частичных сумм алгебраического ортогонального ряда для явной скалярной функции
Надо накатать об этом аж курсач. Нихуя не понимаю, чего от меня хотят. Чем обмазаться?
>Подсчет частичных сумм алгебраического ортогонального ряда для явной скалярной функции
Надо накатать об этом аж курсач. Нихуя не понимаю, чего от меня хотят. Чем обмазаться?
Я в шоке с этих математиков. Только что в книжке расписывал кванторы очень детально, хотя они и так ясны, но внезапно зашибал интеграл без пояснений.
Ребят очень прошу, докажите что предела не существует здесь. lim n->inf n*abs(sin(n))
И вот ещё доказать пикрелейтед.
Пожалуйста.
Аноны, поясните: если предел равен бесконечности, то грамотно ли будет сказать, что предела не существует?
Впервые вошел в раздел(!) и не создал отдельный, а сразу с вопросом сюда. Сейчас школьник 11 класс, где-то до 7-8 хорошо было и с геометрией, и с алгеброй. Менял школы, и теперь я вообще нихуя не понимаю на уроках и уже давно так класса с 10, даже вопрос уместный задать не могу, ни то что решать что-то.
Суть: какие книги по алгебре и геометрии мне нужные, самые базовые, чтобы и освежить память и дойти до производной,тригонометрии,логарифмов - все то, что мы сейчас как бы прошли, но я ничего не усвоил, а в вузике-то полюбому матан понадобится, поэтому вот. То же самое и с геометрией кстати. Спасибо
Суть: какие книги по алгебре и геометрии мне нужные, самые базовые, чтобы и освежить память и дойти до производной,тригонометрии,логарифмов - все то, что мы сейчас как бы прошли, но я ничего не усвоил, а в вузике-то полюбому матан понадобится, поэтому вот. То же самое и с геометрией кстати. Спасибо
Аленицын-Бутиков-Кондратьев, Дорофеев-Потапов-Розов
Но уже явно поздно, егэ тебе не сдать в этом году.
в ЕГЭ мне только база нужна. Не в этом вообще дело. Просто может я нахуй Перельман, а талант гроблю, не занимаясь
Возможно ли проверить неизвестное число на чётность или нечётность - без использования операций деления и деления по модулю?
Да. Отнимай единицы и считай их. Когда единиц не считается посмотри, каким будет их число чётным или нечётным.
Или ещё можешь взять индикатрную функцию f(x)=abs(sin(pi/2*x)), которая равна нулю при чётных и единице при нечётных.
Э, ну че вы, ёба. Судьба литра пива в ваших руках.
Нет. Предел не существует, если он разный с левой и справой стороны.
колькотам ящик считали с помощью вольфрама, напомни?
> без использования операций деления
> pi/2*x
Пусть дано эн и пусть икс и че равны нулю. Если икс равно эн, то четность эн соответствует четности че. В противном случае увеличим икс на единицу, а че сделаем единицей, если оно было нулем, и нулем, если оно было единицей - и повторим шаг еще раз.
Ну, анон выше то же самое по сути и сказал.
Про производную и логарифмы можешь прочитать в гугле, никаких проблем.
/Тригонометрия для школьников/
x^2+1 = 0 не имеет решений в R. Чтобы решать такие уравнения добавим к R элемент i такой, что i^2 = -1. После этого "добавления" появятся так же числа: 7i, 1+9i... Все такие числа называются комплексными и множество комплексных чисел обозначается: C.
Складываются/умножаются они как обычные двучлены. С делением возникает проблемы, непонятно, что будет если (a+bi)/(c+di). Но если домножить числитель и знаменатель на (c-di), то в знаменателе останется только c^2+d^2 - действительное число, на которое делить уже можно. Операция f(c+di) -> (c-di) называется сопряжением.
Комплексные числа можно представить в виде пары чисел: (a+bi) -> (a,b). Можно нанести их на плоскость и провести к каждому радиус-вектор. Модуль числа z - это длина соответствующего ему радиус-вектора. Аргумент числа z - это угол между радиус-вектором и положительным напр. горизонт. оси. |z| можно вычислить по теореме Пифагора: |z| = sqrt(a^2+b^2); т.к. (a+bi)(a-bi) = a^2+b^2, то |(a+bi)|^2 = (a+bi)(a-bi). Если сложить числа: (a,b)+(c,d) = (a+c,b+d), то видно что складываются они как обычные вектора.
|z1+z2| <= |z1|+|z2|(неравенство треуг.)
|z1z2| = |z1||z2|: sqrt((ac-bd)^2 + (ad+bc)^2) = sqrt(a^2+b^2)sqrt(c^2+d^2) => sqrt(a^2c^2+b^2d^2+a^2d^2+b^2c^2) = sqrt(a^2c^2+a^2d^2+b^2c^2+b^2d^2)
Пусть c1, c2 - два компл. числа, а |c1-c2| - расстояние между ними, |z| = 1, тогда: |c1-c2| = |zc1 - zc2| = |z(c1-c2)| = |z||c1-c2| = |c1-c2| и z0 = 0. Тогда умножение на z - это движение с 1 неподвижной точкой(0), то есть вращение на какой-то угол ф. Пусть Arg(z) = ф1 и z1 = 1, тогда zz_1 = z, то есть вектор z_1 повернулся на угол ф1.
Пусть так же |z| = 1 и Arg(z) = ф. Тогда z можно выразить как cosф+isinф. Пусть |c| = 1 и Arg(c) = п, тогда zc = cos(ф+п)+isin(ф+п) = cos(ф)cos(п)-sin(ф)sin(п) + i(cos(ф)sin(п)+sin(ф)cos(п)). То есть получаются формулы:
cos(x1+x2) = cos(x1)cos(x2)-sin(x1)sin(x2)
sin(x1+x2) = cos(x1)sin(x2)+sin(x1)cos(x2)
В последнем абзаце вся школьная тригонометрия.
Провёл хуем по губам вербиторебёнку. То, что ты говоришь вообще ему нахуй не надо. Дал бы ссылку на вики и то лучше было.
>В последнем абзаце вся школьная тригонометрия.
Нет. Ты не слова не сказал про триногометрическую окружность, графики синуса и косинуса, тангенса и котангенса, тригонометрические неравества и уравнения, свзять с треугольниками и их решения. Вместо этого ты начал поливать всё своей вербитодриснёй.
Почитай школьные учебники, ну ещё и тригонометрию гельфанда. А этого дебила не слушай. Комплексные числа для ЕГЭ не нужны, не трать на них время.
>не слова
*слова - фикс
Блядь. Сонный, вот и мысли сбиваются.
Ну и нагородил же ты своими буквами.
По сути это брут числа.
Можно было бы брутить большими 1 шагами, например шагами размером в 1^N, отнимая 1^N от исходного числа, и сравнивая его с числами, в диапазоне от 0 до 1^N, где последний бит числа в диапазоне явно показывает чётность числа.
Комплексные числа здесь нужны чтобы вывести тригонометрические тождества. В школах это дается через подобие треугольников, что занимает много времени и в итоге большинство нихуя не понимает и просто пытается запомнить эти формулы(у меня кстати не получалось их запомнить) оттачивая на миллиарде примеров аля: вычислить cos(75). Поэтому я и написал, что всё что нужно есть в сообщении. Графики и окружность нужны, ещё измерение углов в радианах нужно. Но всё это можно быстренько рассказать нарисовав картинку.
По поводу тригонометрии Гельфанда, ты её сам читал? Книга ахуенная, но довольно сложная, если он на уровне 8-9 класса то скорее всего он её бросит. Формулы суммы углов там вводятся с помощью скалярного произведения векторов, что не легче и не сложней способа через комплексные числа.
Почему на русском так мало годных книг? Мало того, что стиль изложения отвратительный, так и все были изданы еще хуй знает когда.
Дайте материал типа вспомнить все. Мол, начали с палочек, далее указали числом рядом с палочками. И так наростает и дошли до интегралов.
Чем вы тут занимаетесь? Какие синусы косинусов? Что за тригонометрия Гендальфа? Почему надо мерить грани куба, вырванного под квадратный корень? Чему равен x? Кто убил Ньютона? Что происходит?
Какие разделы математики я должен знать, чтобы вкатываться в криптографию?
Как минимум общую алгебру.
Теория информации, теория кодирования, теория вычислимости, теория вычислительной сложности, теория колец, теория полей, теория групп, можно еще алгебраической геометрии на пол-шишечки.
>Кто убил Ньютона?
этим человеком был Альберт Эйнштейн
Дайте гайд по разложению функции в ряд Фурье на рандомном промежутке. Я нихуя не понимаю из учебника ><
youtube://wildberger+math+foundations
я в целом хочу прокачать себя в математике, вне зависимости от тем наличествующих в ЕГЭ, но начинать мне необходимо с азов, поэтому вместо объяснения вещей, которые мне не понять в силу отсутствия некой базы, великолепным бы был исход, где мне бы был рекомендован фундаментальный математический труд, вмещающий в себя основные вещи школьные хотя бы, ну и что-то уходящее чуть дальше, но не обязательно. Хочу в целом математику знать, понимать ее место среди наук, чтобы хоть как-то отвлечься от ее абстрактности и пустой необходимости заучивать формулы, без понимания, где это, что это, зачем и куда. Чтобы бв и интеллектуально как-то качнуться, это ведь нагружает хорошо мозг, значит, это мне интересно
Хули вы на конктретные вопросы не отвечаете? Как школьники-космологи из спц, которые не могут квадратный корень из восьми взять, но зато поясняют за чОрные дыры.
Возможно ли, каким-то образом, с помощью операций умножения, сложения и вычитания,
найти неизвестное число,
являющееся множителем известного вектора-произведения на другой известный вектор?
Но у него же секта без рациональных чисел.
С рациональными.
интегральные уравнения Вольтерра: Ребят, можете объяснить, откуда в последней строке y(x)?
Что я делаю не так?
Вроде как должна была получиться
единица
Всё, понял.
Анон, здрасте.
Есть задача подготовиться к ЕГЭ. Познать, так сказать свои пределы.
Посоветуй литературы пожалуйста?
Сам я ВПЛ, если это важно, уровень знаний: знаю как делить в столбик
Есть задача подготовиться к ЕГЭ. Познать, так сказать свои пределы.
Посоветуй литературы пожалуйста?
Сам я ВПЛ, если это важно, уровень знаний: знаю как делить в столбик
А ну и под ЕГЭ и заточен, это, наверное, лучшее, что можно посоветовать
За Ткачука спасибо, но он начинает с тригонометрии, явно для уже крепко знающих или помнящих основы.
Помогите с чем-нибудь. Умоляю
Привет, господа, если вы решите мне хоть что-то из пикрелейтед, я буду Вам очень благодарен
273 лови
Прости, ты из какой-то трендовой англоязычной школы, где грамматику и лексику дают в перерывах, а потом пичкают вот этими счетоводными задачами, ублюдническая повторяемость которых любого здорового человека (а молодого/юного тем более) до смерти доведёт? Или это у вас в университете (что очень маловероятно)? На что вообще может быть рассчитан курс ВОТ ЭТОГО? Обидеть не хотел.
еще 2 лови
Спасибо огромное. И я хотел спросить, насколько вообще доверять ходу решения wolframalpha? По-моему там как-то упорото всё. Например решение пикрелейтед.
В 273 походу ошибка, я позже посмотрю и поправлю
Сап математики. Кто-нибудь может решить подобное?
Я могу. Просто по определению решай.
273 переделанный. Проебался с подстановкой. Ответ получился правильный, но решение говно.
Сознательно довести элементарные вычислительные операции до автоматизма так, чтобы их выполнение вошло в подсознание.
Многократным повторением...
HAL 9000, залогинься.
Парни а ошибкой ли будет в определении предела написать нестрогое неравенство вот такое типо abs(x(n)-A)<=epsilon ? По моему нет, это ведь просто будет значить включить ещё одно значение которое попадает на границу эпсилон радиуса предела. Но почему так нигде не пишут
собственно, заменить открытый шар на замкнутый и ничего не изменится.
Подскажите как можно начиная с (b) делать. Долго ломаю голову но чет плохо факторилизация полиминалов двется.
http://nasha-sasha.livejournal.com/420806.html?thread=6907846
Отсчёт о том, как Вербита мукой обсыпали.
Отсчёт о том, как Вербита мукой обсыпали.
Что это за быдло?
И рэпера из Лондона Оксимирона
Что такое 'картофан' ?
Современная математика, теория категорий, алгбераическая топология и геометрия.
Возможно ли изучать алгебру, но не лезть в анализ дальше производных?
Львовский охуел. Как к этому подступиться?
Sin(x)=(1-sqrt(5))/2
Я думал, что хорошо школьный курс помню.
Sin(x)=(1-sqrt(5))/2
Я думал, что хорошо школьный курс помню.
золотое сечение не узнал?
Узнал. В соседнем примере другой знаменатель прогрессии с +, вместо -. Но как от этой хренаны арксинус брать я не знаю.
одно Ф, другое 1/Ф. Попробуй осмыслить геометрически.
Посоны, define "картофан" в контексте доски, пожалуйста.
Изначально: матанализ каким его учат на мехмате в МГУ (пользуясь абстракциями начала 20-го века). Постепенно эволюционировало до пренебрежительного ярлыка для прикладных задач и методов, которые не привносят в современную математику ничего нового сами по себе.
Фанатики используют как синоним к "модно", "современно" и даже "хорошо".
>Фанатики используют как синоним к "модно", "современно" и даже "хорошо".
В смысле наоборот.
Фанатики используют как синоним к "не модно", "не современно" и даже "не хорошо".
быстрофикс
О, спасибо.
b) равен нулю при x=y,z=x...
e) тоже самое при a=-b
остальные небось какими-то трюками. c) можно попробовать поделить на a+1, a^2+a+1
>(b)
Превращаешь изначальное говно в пикрилейтед.
А как понял что нужно xyz прибавлять?
Сап, нужна помощь по геометрической задачке.
Треугольник ABC вписан в окружность.Хорда AD этой окружности является биссектрисой треугольника ABC и пересекает BC в точке L.Хорда DE окружности перпендикулярна стороне AC и пересекает ее в точке K. Найдите отношение AK/KC, если BL/LC =0,5
Треугольник ABC вписан в окружность.Хорда AD этой окружности является биссектрисой треугольника ABC и пересекает BC в точке L.Хорда DE окружности перпендикулярна стороне AC и пересекает ее в точке K. Найдите отношение AK/KC, если BL/LC =0,5
Гугли книгу "Кортафанская геометрия для превращения человека в калькулятор, 2016-2017". Очень популярная книга в российских школах.
Не все симметричные матрицы такие, а лишь какое-то подпространство.
Как найти длину проекции вектора на прямую, если проекция не перпендикулярная к прямой?
Например, есть прямая с наклоном к оси иксов 30 градусов, и есть вектор с углом 45 градусов к оси иксов. Как найти его проекцию на прямую?
Сперва найти перпендикулярную проекцию на ось иксов а потом с оси иксов так же перпендикуляром на прямую?
Объясните мне, что вообще здесь происходит, является ли это конечным примером или его нужно решить? Задали по программированию на c++
Это разложение в ряд -e^(-x)
А что за задание у тебя -- тебе лучше знать. Возможно реализовать функцию, которая с помощью такого ряда считает значение экспоненты в любой точке с заданной точностью
>Как найти длину проекции вектора на прямую, если проекция не перпендикулярная к прямой?
>Например, есть прямая с наклоном к оси иксов 30 градусов, и есть вектор с углом 45 градусов к оси иксов.
А проекция какая?
Рилейтед список валиден для того, кто проебал школьный курс полностью? Xотел начать с алгебры Гельфанда и геометрии Калинина.
Вполне. Если проебал совсем капитально, то добавь еще Сканави. Там много задач, прорешай побольше, чтобы в голове как следует уложилось.
Спасибо, анончик. Завтра же начну менять своё будущее. Как думаешь, школьный курс за полгода это фантастика?
Ты ебанутый? Решаешь алгебру Гельфанда, потом берешь Алексеева "Теорема Абеля в задачах и решениях". Из геометрии школьной нужно знать только теорему Пифагора, векторы, движения. По ТМ можешь прочесть английскую вики.
забыл ещё тригонометрию нужно. Гельфанда тригонометрию можешь взять.
Проекция в первом случае под углом к прямой, не перпендикуляр в пи/2.
>школьный курс
>Теорема Абеля
Это от создателей "бурбаки нужно в детсаду преподавать?"
> Фейман изучил матанализ в 13 лет
Способности к феноменальному счёту у Игоря Алексеевича Шелушкова из г. Горького (ныне Н.Новгород) проявились в 9-м классе школы (60-е годы ХХ в). Учителя предупреждали его о возможной перегрузке психики при неограниченном увлечении скоростным счётом, но Игорь не прислушался к советам по релаксации и отдыху. Первые несколько лет всё шло хорошо: поступил и успешно закончил Горьковский политех, стал в нём аспирантом, а затем преподавателем. Всё чаще и успешнее показывал свои способности к устному счёту, начал совершать гастроли по стране, а потом получил приглашение выступать и за границей. О нём писали в газетных и журнальных статьях (в частности, В. Д. Пекелис). Но через непродолжительное время упоминания о Шелушкове исчезли из печати, а он сам оказался на много лет в одной из психиатрических больниц, стал инвалидом. Вывод очевиден: И. Шелушков стал жертвой неграмотной и неумеренной нагрузки на нервную систему, своего рода «жадности» к использованию проявившейся у него выдающейся способности к счёту, мгновенному подсчёту числа букв в тексте, запоминанию таблиц логарифмов и т. д.
Тао и Нейман в ~8
Миша в 13 ходил на семинары Гельфанда в МГУ
Труъ пацыки из топологического трэда к 14 годам прочитывают алгтоп Хуйтчера
А есть какой-нибудь паззл Рубика с группой Ли?
Умер от избытка картофана в организме?
>A swimming pool is divided into 2 equal sections. Each sections has its own water supply pipe. To fill one section (using its pipe), you need a hours. To fill the other sections you need b hours. How many hours would you neeed if you turn on both pipes and remove the wall dividing the pool into sections?
Оцените решение. Возьмем половину бассейна как 1 юнит.
Первая руба ебашит со скоростью 1/a units/h , вторая 1/b u/h.
Если убрать стену, то общая скорость будет 1/a+1/b u/h.
Так как у нас 2 юнита, значит весь бассейн = 2. Получаем уравнение (1/a+1/b)*h=2
значит кол-во часов для заполнения всего бассейна :
h=2ab/(a+b)
Оцените решение. Возьмем половину бассейна как 1 юнит.
Первая руба ебашит со скоростью 1/a units/h , вторая 1/b u/h.
Если убрать стену, то общая скорость будет 1/a+1/b u/h.
Так как у нас 2 юнита, значит весь бассейн = 2. Получаем уравнение (1/a+1/b)*h=2
значит кол-во часов для заполнения всего бассейна :
h=2ab/(a+b)
Ни одного упоминания гомологии, очень недоволен тобой
Что с пикрил?
Все очень просто. Я дам ему 6 рублей, он даст мне 5. Итого у него рубль профита. И буду так делать пока у него 19 рублей профита не останется.
Я б еще жовки взял, или флэша бутылочку
>6×19 - 5×19 = 114 - 95 = 19
Объемы обменной операции не очень оптимизированы.
3x - 5y = 19;
3x = 19 + 5y;
x = (19 + 5y)/3;
инкремент y, пока x не станет целым.
y = 1; x = 8;
>3×8 - 5 = 19
>Объемы обменной операции не очень оптимизированы.
Зато кассиршу знатно потроллю
Чот весь этот пиздос мне напомнил дореволюционну книжку какой-то барышни, там еще первая задачка про золотой крест и брильянты. Уж даже и не знаю почему
http://www.myshared.ru/slide/626757/
Куда репортить
Куда репортить
Что за пздц? У этого вообще существует разумное решение?
Чет вообще не могу догнать
Репортить бессмысленно - все мочераторы на художественной гимнастике.
(Автор этого поста был забанен. Помянем.)
Возведи x+1/x в квадрат.
(a) корень из семи?
мимо великий математик
Токие няши. Вот еще бы не срались ине ссались бы первые зать лет, цены бы небыло
Ну йобана, 30 минут ломал голову.
Аноны, подскажите, какой раздел математики самый-самый фундаментальный выражаясь программистским языком, самый низкоуровневый?
Арифметика, не?
Мои познания в математике весьма малы, но я могу сказать что даже теория множеств ведь пофундаментальнее арифметики, не?
Фундаменталка это pure abstraction. Это циферки , сложение материи и пространства, вычитание материи.
Скачай рабочие программы с сайта министерства образования. А лучше грызи "Начала" Евклида.
>выражаясь программистским языком, самый низкоуровневый
Грызи систему команд процессора.
Алсо, математика и есть же.
Математика — фундаментальная наука,
предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы.
По определению.
низкоуровневый: комбинаторика
фудаментального одного нет, есть набор сюжетов, которые Атия называет
core mathematics, и который настолько тесно связан со всем остальным,
что его знание позволяет тебе ориентироваться в происходящем в науке
вцелом. во всяком случае, пытаться.
включает в себя (примерно) теорию Галуа, абелевы категории и
гомологическую алгебру, коммутативную алгебру, эллиптические
операторы, уравнение Монжа-Ампера, теорию схем, этальные когомологии,
теорию полей классов, теорию Ходжа, теорию деформаций, группы и
алгебры Ли, теорему Хирцебруха-Гротендика-Римана-Роха-индекса,
наверное, Д-модули и K-теорию. Атия не имел в виду, но с тех пор
времена изменились, и наверное в арсенал нормального математика
теперь входят начатки метрической геометрии и геометрической теории
групп, эргодическая теория и теорема Ратнер, что забыл?
Анон, довольно серьезная проблема. Сыну 9 лет, и я чет по приколу год назад начал ему перед сном читать математику, начал с гелфланда. Я думал ему станет скучно и он будет быстро засыпать, а он блин с интересом слушает, задачки в уме решает. Сейчас после года такого чтения мы уже с ним на калкулусе спивака и я реально начинаю его бояться. Он же в 10 лет станет более развитым в математике чем я и мне больше поговорить с ним не о чем будет даже, с его то быстрым развитием. Ну вот и реквестирую какой-нибудь книги, которая будет математической, но которая не будет его развивать, просто быдло вычисления по формулам, чтобы он меня умнее никогда не стал, и я мог по уровню всегда выше его быть. Желательно побольше таких книг. Он ато без математики на ночь не может заснуть.
Чет так и вижу заголовок в "Пусть говорят" : "Отец все детство делал из сына картофана"
Ты хочешь сказать, что твой сын в 9 лет щелкает интегральчики в уме как штатный садовод-картофолог?
Да, я сам в ахуе сижу. Мне срочно нужно его уровень понизить, я чувствую что скоро я его потеряю как собеседника.
Вот даже вчера я зашел в его комнату чтобы позвать сходить в кино на мультик, а он сидел спивака читал, и мне говорит что не хочет зря время терять в кино. Ну это уже перебор я считаю. Может мне у него все книги/тетрадки отобрать и насильно его заставлять гулять с нормальными детьми? Он же не социализируется сейчас и потом всю жизнь страдать будет, и для меня он все больше и больше отдаляется в свой мир математики. Я думаю ему и школьной математики за глаза хватит, ему же все равно для аттестата только.
>я реально начинаю его бояться
Сам себя накрутил и сцыт. Нахуй так делать?
Грызи лучше сам, на опережение, всю программу Вербицкого, раз ты такой...
http://verbit.ru/Job/HSE/Curriculum/all.txt
http://imperium.lenin.ru/~verbit/MATH/programma.html
Поговори с ним о математике в контексте его области интересов. Намечается ли у него какое-то особое видение того, что он изучает, решает. Спроси насколько это для него важно. Выясни его систему взглядов на математику. Попытайся понять, из чего это происходит. Сделай из простых чтений этих задач нечто дискуссионное, что способно будет его немного встряхнуть. И главное, чтобы у него эмоциональность не стала зависимой от чистки картофеля. А книги посоветую ровно те, что сука, и я это говорю в /math/ далеки от математики. Фикшн, короче. Если ты вообще начал его приобщать к хорошему книжцу.
> И главное, чтобы у него эмоциональность не стала зависимой от чистки картофеля.
Вот тут не понял. А при чем тут картошка?
> картофан
Дай названия книг Гельфанда и Спивака, плиз.
Анон, объясни смысл математики. Учусь на программиста. В школе приходилось решать однотипные задачи, где видишь пример и применяешь определённый алгоритм решения. Думал, что в универе будет по интересней, но нет блядь, продолжаю решать такие же однотипные задачи. Такое чувство, что из меня выращивают калькулятор, хотя очевидно, что машину превзойти я не смогу. Говорят, что математика развивает логическое мышление, но чтобы иметь хорошие оценки в моей шараге (дело не в шараге, а математике на инженерных специальностях) даже среднячком не нужно быть, а просто зазубрить возможные решения ряда примеров.
У меня такое чувство, что от меня всю жизнь прячут математику... Не ужели подражание калькулятору хоть чем-то полезно и это и есть математика, хоть и в узком понимании....
У меня такое чувство, что от меня всю жизнь прячут математику... Не ужели подражание калькулятору хоть чем-то полезно и это и есть математика, хоть и в узком понимании....
M.Gelfand Algebra
Spivak. Calculus
В российских вузах учат калькуляторству, смирись с этим. Математика есть в учебниках, оп-книгах, etc.
По-ангельски читаешь ему что-ли?
Ну да, на более менее нормальном уровне лет в 7 знали уже.
Кто такие картофан?
Второкультурщики
А кто такие второкультурщики?
Ну что за пездос творится
https://www.youtube.com/watch?v=Ozw4_L3TiBM
https://www.youtube.com/watch?v=Ozw4_L3TiBM
Те, кто занимается теорией категорий, гамалогиями и тапалогиями.
Вот полная лекция https://www.youtube.com/watch?v=KoVBe5ikgHQ
Не полная
Перекат.
https://2ch.hk/math/res/5474.html
https://2ch.hk/math/res/5474.html
выделить главную часть вида Cx^k при k->0 функции на пике. я прав? мне кажется, что нет. помогите
Как решать уравнение x^x = a?









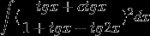



















































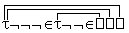






































Также приветствуется обсуждения самого процесса изучения и учебников/задачников
Архивы тредов
http://pastebin.com/kiRZGVHW
ВНИМАНИЕ! ВНИМАНИЕ!! ВНИМАНИЕ!!!
On-line LaTex. Формулы пишем в нём, а после прикрепляем картинками к посту
http://www.codecogs.com/latex/eqneditor.php
Львовский Набор и вёрстка в системе latex
http://www.mccme.ru/free-books/llang/newllang.pdf
Если ты только зашел в тред и хочешь спросить, какую книжку прочитать, то ответ, скорее всего, будет в этих списках, анон.
Список от ОП-а, бывшего тут до меня. Был составлен на протяжении 13 тредов, к ознакомлению обязателен.
http://pastebin.com/4iMjfWAf
Список от анона с dxdy. Довольно внушителен, тоже рекомендуется к прочтению. Является дополнением к списку старго ОП-а.
http://pastebin.com/YP1uaUyd
Goodbook.txt список книг с dxdy, рекомендованный тамошними обитателями.
http://pastebin.com/4FngRj6n
Литература - НМУ
https://docs.google.com/spreadsheets/d/1UWwIIAFwSwOQLK3m--LOaMOvHUivFDEz-JAnLa87i7Q/edit#gid=0
ОП-список 2. Составляйте список в реальном времени! Предлагайте в тред книги, критикуйте уже имеющиеся!
http://pastebin.com/szzZfkCM
Форчановский список, книги на английском.
http://4chan-science.wikia.com/wiki/Mathematics
Список с видеолекциями(в разработке):
http://pastebin.com/S3d7Jj6J
Качать книги тут:
http://libgen.io
А статьи тут(в разработке):
http://pastebin.com/3BfHPskz
Мемасы(в разработке):
http://pastebin.com/e38Yuj5V
СПИСКИ В РАЗРАБОТКЕ, НУЖНА ПОМОЩЬ АНОНА, ПОЖЕЛАНИЯ ОСТАВЛЯЕМ В ТРЭДЕ