Почему степень многочлена считается именно так?
Аноны, вы когда-нибудь себя мотивировали решать задачи и вот просто набивать руку по определенной теме? Знаю, что заставлять себя и нехотя пытаться решать упражнения, - все это путь в никуда, ведь должен же быть какой-то интерес. У меня какое-то ебанутое состояние, я очень хочу получать новые знания, а вот задачи решать ну пиздец руки опускаются, а если они ещё и нестандартные какие-то, то все. Вообще, конечно, все достаточно просто. Хочешь - решай, не хочешь - пиздуй, но я не могу понять как совладать с собой и просто получить удовольствие от решения задач.
>14888
>1488
>1488
Я пытаюсь решать задачи, чтобы лучше вникнуть в тему. Пока несколько задач не прорешал нет ощущения, что разобрался. Зато после задач приходит уверенность и лучшее понимание теории.
Анон, странное дело, но иногда бывает так, что ты можешь понимать что-то, не решая и не зная практически ничего по теме. Берёшь какую-то задачу из какой-нибудь теории чисел и внезапно для себя можешь её решить на интуиции, не зная ни методов, ни самой темы. Но такое бывает редко и полагаться на это не стоит.
ну с такими вопросами тебе скорее в психач
>они ещё и нестандартные какие-то, то все
А разве задачи без прошивки - это не самое интересное? Вот решать упражнения в промышленных масштабах - это пиздец.
>заставлять себя и нехотя пытаться решать упражнения, - все это путь в никуда
Нет. Главное решать, от твоего душевного состояния зависит примерно ничего. Если лень - значит борись и терпи. Всё. https://2ch.hk/psy/
Палю тебе секрет успеха многих деятелей науки.
Разреши себе фап только после выполненного упражнения. Если нарушишь, то бей по яичкам. Сильно. Чистая физиология.
Во время фапа часто приходит решение задачи.
Не у таких людей как автор поста, которые их скипают
Я к тому, что не обязательно после, давно использую это, когда не даётся задача,в тот самый момент приходит решение. На самом деле как-то неловко о таком писать, красный как рак сейчас сижу.
Но это работает.
Архивач: http://arhivach.org/thread/254519/
Это может работать для тех у кого уже есть внутренняя дисциплина, а не для тех у кого проблемы с волей.
Да, конечно, просто упомянули про фап и научников решил тоже написать.
Да какой психач, там просто люди накручивают себя выдуманной хуйней всякой. Я, видимо, плохо пояснил. Выше анон правду написал, что мотивация решать задачи - понять материал. А вот как получить удовольствие в ходе этого процесса, разве все, кто так или иначе занимается математикой постоянно превозмогают и уговаривают себя? Такого быть не может.
Анон, в общем есть такая проблема, у меня матан ведет чокнутая старушка, которая уже в маразме и не совсем понимает что происходит вокруг нее. В общем из каждого экзамена, а я сдавал ей в зимнюю сессию, она устраивает какой-то цирк, экзамен начинается в 10 утра, а заканчивается в 9 вечера. Так вот, чтобы получить у нее тройку нужно знать доказательства теорем, а перед этим решить задания (что-то типа допуска к теоретическим вопросам). Сейчас у меня идут ряды, числовые, функциональные, фурье и т.п. и я хотел спросить, есть ли где-нибудь хороший учебник по математике, где хорошо изложены вышесказанные темы?
Фихтенгольца не предлагать, читал, не очень понравилось. Подойдут в принципе книги и на англ. языке.
Фихтенгольца не предлагать, читал, не очень понравилось. Подойдут в принципе книги и на англ. языке.
Так, давайте еще раз.
Дифференцируемость функции это возможность замены функции бесконечно малыми прямыми отрезками.
Дифференциал это уже именно замена функции в каком то месте таким отрезком.
Производная это разложение дифференциала по осям, с делением этих разложений друг на друга.
Интеграл это сумма последовательных дифференциалов на каком то отрезке функции.
Все так или нет?
Калькулус тотомаса, понарин, лекции босса, ильин позняк, понтрягин
Как задать квадратичную форму в заданном базисе?
p.s. Вместо a подставьте 16.
p.s. Вместо a подставьте 16.
Куранта почитай.
ЭТО ЧТО ЗА НЕВМЕНЯЕМОЕ СУЩЕСТВО?
Зачем ты пытаешься консультировать по вопросам, в которых сам нихуя не понимаешь? Ты же тупое нулевое говно, натуральный идиот.
Не слушай шизика. Твой вопрос уже миллион раз обсуждался в каждом уголке интернета, а ты ленивый хуй даже не удосужился погуглить. У нас был отдельный топик
Годный учебник? Какой-нибудь порог вхождения есть?
Хорошо, спасибо анон, загляну в тред и прочитаю, если найду что нужно, то постараюсь больше не срать тут у вас.
Для начинабщих простым языком без топологий и гомологий. Даже множеств нет.
Дифференциал в точке - это бесконечно-малый отрезок касательной к графику в этой точке.
Производная - это угловой коэффициент этого отрезка. Всякая прямая описывается уравнением y=kx+b, вот производная - это k.
Интеграл - это сумма бесконечно-малых прямоугольников, у каждого из которых основание - дифференциал аргумента, высота - значение функции.
>Калькулус
Матаны, а почему в буржуйской литературе calculus и analysis считаются разными вещами? Что есть что тогда?
>Дифференциал в точке - это бесконечно-малый отрезок касательной к графику в этой точке.
Замена графика кривой прямой
>Производная - это угловой коэффициент этого отрезка. Всякая прямая описывается уравнением y=kx+b, вот производная - это k.
Может тангенс, а не угловой коэффициент? Иначе у функции у=х наклон 1 выражается в попугаях.
>Интеграл - это сумма бесконечно-малых прямоугольников, у каждого из которых основание - дифференциал аргумента, высота - значение функции.
Предел суммы дифференциалов
Аргументированный ответ почему книжки плохие.
Что-то я путаюсь сильно в модульной арифметике. Вы ее на зубок знаете? Я и признаки делимости-то не могу вывести или достаточно просто знать, что такое есть и если что поискать? Как делать с этим всем? А то какая-то китайская грамота... На часы глядеть?
Где почитать про то, как уравнения с двумя переменными решать?
Почему нищая и обоссаная лурочка советует мне книжки лучше чем уважаемые, по своему собственному мнению, математики с харкачей?
calculus — это часть анализа. По русски калькулус — анализ бесконечно малых. Сам анализ(как раздел) включает себя анализ бесконечно малых, функциональный анализ, теория меры...
Какие, например?
>calculus — это часть анализа. По русски калькулус — анализ бесконечно малых. Сам анализ(как раздел) включает себя анализ бесконечно малых, функциональный анализ, теория меры...
Век живи век учись! Спасибо.
2 десятка 5 десятков = 10 десятков = 100
НО ВЕДЬ! Это тоже самое что 2050=1000
Поясните. Это баг или фича?
Это вакаба. Иди с миром.
2 десятка (умножить) на 5 десятков = 10 десятков = 100
НО ВЕДЬ! Это тоже самое что 20(умножить)на 50=1000
Фикс.
>2 десятка (умножить) на 5 десятков = 10 десятков
Не равно. Равно 10 десятков десятков=1000.
Бамп.
Какой математический аппарат надо для понимания и применения p-адических чисел?
И посоветуйте, пожалуйста, что-то по модульной арифметики (разные уровни, да?).
И посоветуйте, пожалуйста, что-то по модульной арифметики (разные уровни, да?).
Здесь мало специалистов если вообще есть по теории чисел, здесь в основном алгебраисты.
Для понимания p-адических чисел достаточно мозгов, там определение очень простое. Ну, желательно знать, что такое норма и что такое метрика, порожденная нормой.
Это пэ или что за пуква?
пэ адические
Это буква пэ.
Лузина и задачник бермана.
Это простые книги же было бы странно, если бы ты не их понять. Вместо того Бермана взял бы лучше Демидовича, я даже уверен, что большинство задачь от-туда взято.
Почему тогда под реквесты не советуют его?
Я помню, взятие интеграла это математический спид, математики не считают а устанавливают изоморфизмы и т.д.
Книга может и не плохая, но для своих лет. Сейчас есть книги короче и с топологиями.
> Сейчас есть книги короче и с топологиями.
>Это простые книги
Зато новые книги сложные. А всё гениальное просто.
Рудин не сложный.
Похоже, что вас двое тут.
не понял
Сап, матанач. Решил изучать математику, но в 90% учебников натыкаюсь на такое, что вроде сначала все ясно, а потом ВНЕЗАПНО тебе выдают что-то, что выглядит как тезис основанный на других областях высшей математики, хотя об этом нигде не упоминается, который перегружен одновременно кучей разных понятий. Мои предположения небезосновательны или я просто даун, который трудно вникает в информацию? Пример на 1 и 2 пиках.
>о в 90% учебников натыкаюсь на такое, что вроде сначала все ясно, а потом ВНЕЗАПНО
Так будет всегда. Привыкай.
https://www.youtube.com/watch?v=duVq7cXWcYw
Такое может быть, но на пиках этого не вижу, так что скорее всего
>просто даун
То есть моего школьного бэкграунда должно быть достаточно для изучения таких вещей?
Опять про возраст. За 70 лет действие + и - изменились? Что за рыбникизация?
И раз есть такие же, с топологиями, множествами, векторным анализом и функциональным анализом, с доступным изложением то давай пиши их сюда.
инб4 курант/зорич/рудин
Разницы нет, только на первом пике всё записано словами, а на втором не всё записано словами. Может быть, что это такая зрительная иллюзия, ты боишься незнакомых обозначений, мозг сразу метит это как "сложная математика из фильмов", а на самом деле если это запихнуть куда-то поглубже и начать разбираться выяснится, что ты всё понял.
Ты про кванторы знаешь?
Что конкретно тебе непонятно в том, что ты скинул?
Нет. В данном случае я привел пример непонимания, но вообще интересно, что стоит почитать чтобы убрать разрыв между школьной математикой и вузовской.
Грубо говоря, есть язык сокращённой записи в математике: всякие "существует", "любой", "такой, что" и так далее, он используется повсеместно. Например, вот тут можешь почитать об этом.
http://mathprofi.ru/osnovy_matematicheskoj_logiki.html
Но я не уверен, что у тебя именно в этом разрыв, это моё предположение было. Что конкретно тебе там непонятно?
Мне даже стыдно отвечать, потому что прямо таки много чего. Может сейчас разум помутнен из-за сонливости, но завтра попробую сформулировать .
Нет, там мало по ссылке, не ходи. Я не могу найти где видел короткую табличку что есть что.
Рудин хороший, и не занимает 9томов. Почему здесь любят Зорича, я не понимаю, мех-мат ст@йл же.
Нет никакой "высшей", "вузовской", "школьной" математики. Т.к. их нет, то и разрыва между ними быть не может. Забудь эти словосочетания.
Хз, лучше ничего не могу найти
https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BE%D0%B1%D0%BE%D0%B7%D0%BD%D0%B0%D1%87%D0%B5%D0%BD%D0%B8%D1%8F
В общем, если дело в обозначениях разберись в них, потом попробуй перевести на естественный язык и если после этого всё равно будет непонятно, тогда уже пиши.
>За 70 лет действие + и - изменились?
Смотри, сама математика не изменилась, но тогда стране нужны были паровозы, отсюда сильно прикладная подача материала, то есть само отношение к науке(не только математике) тогда было сильно прикладным, наука должна обслуживать интересы пролетариата, быть инструментом построения коммунизма, являться самодостаточной ей вредно, наверное это имеется ввиду. Учась по таким учебникам ты прививаешь себе нехороший образ мышления. Но это неточно.
С другой стороны не думаю, что многих это устраивало, и авторы тех лет могли писать учебники с таким подтекстом, что вот
https://ru.wikipedia.org/wiki/%D0%9A%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D0%B8%D1%8F:%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B8_%D0%A1%D0%A1%D0%A1%D0%A0
Существует школьная математика.
Существует вузовская математика: синоним "высшая".
Также существует математика.
Все три не пересекаются.
>Все три не пересекаются.
Э?
Пересечение школьной математики и высшей математики пусто.
Пересечение школьной математики и математики пусто.
Пересечение высшей математики и математики пусто.
>Пересечение школьной математики и высшей математики пусто.
Функция синуса.
>Пересечение школьной математики и математики
Школьнвя математика.
>Пересечение высшей математики и математики
Высшая математика.
https://www.youtube.com/watch?v=3sQBGGn5VsY
Синус из школьной математики и из вузовоской математики - это два очень разных синуса.
Ни школьная, ни вузовская математика не входят в математику.
> это два очень разных синуса
Синус может быть только один. Да и синус просто контрпример, а так пересечение школьной и высшей школьная. Вот и получается, что есть одна большая математика, просто ты её частями знаешь.
>-- Вторая свежесть -- вот что вздор! Свежесть бывает только одна -- первая, она же и последняя. А если осетрина второй свежести, то это означает, что она тухлая!
Не нравится синус пусть будет единица.
Или "+". Ну ты понел. Что-то ты совсем, короче.
Простой и самоочевидный язык же. Иногда даже забавный. Просто понимать это лично я стал лишь когда выгнали из вуза, лол. Раньше тоже охреневал, потому что ничего не учил и не хотел учить, а двачевал и игорял.
Рудин довольно жесток для новичка. Сжатый, с упором на общие определения взамен частных, во введении к русскому изданию все написано. Не смотрите на то, что там 300 страниц, ведь каждую страницу придется переваривать весьма долго. Чем вам тот же Курант не угодил, я не знаю, как по мне весьма приятный курс.
Алсо, не все в восторге от Рудина.
>Vladimir Arnold, one of the champions of the “organic” approach to mathematics, reportedly called the book (in comparison to the lectures of Vladimir Zorich) “Bourbakian propaganda, stripping and sterilizing analysis of any soul or meaning beyond the symbols.”
> stripping and sterilizing analysis of any soul or meaning beyond the symbols.
Хм, он упрекал их в том, что они пытаются заглянуть в душу математики, систематизировать, рационализировать душу вместо того, чтобы? Верить? Типа Бурбаки убивают магию математики? Что-то у меня совсем иные представления были о "дедах".
Ну, Арнольд был довольно эпатажным товарищем. Можешь почитать его статьи, чтобы понять, о чем речь, и не пороть чушь.
Возможно.
Сомневаюсь что тебя не сделал батя с коммунистическим подтекстом.
В каком смысле?
+ из школьной математики и + из вузовской - два разных понятия. Равно как 1.
>Равно как 1
И в чём по твоему разница?
В школе единица - это символ, который можно писать на бумаге и действия с которым можно производить согласно таблицам сложения и умножения.
В университете 1 - это элемент множества с некоторой структурой.
> это символ, который можно писать на бумаге и действия с которым можно производить согласно таблицам сложения и умножения.
Это и для университета верно.
Нет.
Как это нет если да. Это не символ? Его нельзя писать на бумаге? Нельзя производить действия?
Множествопидора ответ
Содомит.
Если бы это было так, то в вузе бы изучали таблицу умножения. Этого не происходит.
Как из того, что это символ, который можно писать на бумаге следует то, что в вузе должны изучать таблицу умножения? Ты не болен, случайно?
Если бы в вузовской математике единица понималась бы как символ, то её изучение повторяло бы изучение единицы в школе. В частности, в вузе бы изучали таблицу сложения и таблицу умножения.
А что делать если максимум, что я могу это распознавать математику и некоторые выражения да подсчитывать чуть-чуть, но сам творить и не умею?
Если бы в строительном деле кирпич понимался бы как элементарный строительный блок, то все здания были бы одинаковыми.
Смотреть стримы доты.
Но обрушились бы без фундамента.
Это меня еще труднее заставить, чем учить математику.
Ну да. Они же одинаковые.
Тогда купи гитару и учись играть. Смотри, как чувак умеет, улетаешь натурально.
https://www.youtube.com/watch?v=7gphiFVVtUI
Так без таблеток никак?
Не знаю, это доктор решает. Может быть и как. Всё зависит от твоего состояния.
Возражай по существу. Аналогии не нужны, потому что любую вещь можно уподобить любой вещи и получить любой результат.
>Если бы в вузовской математике единица понималась бы как символ, то
Из первого не следует второе.
А если бы математика имела запах то как бы она пахла?
Ну, я и дурак. Так поставил вопрос неправильно. Что поделать.
Следует. Символ всегда даётся в совокупности с правилами оперирования им.
Здесь запрещён оффтопик. Пока тебя никто не зарепортил, но если ты не угомонишься кто-нибудь обязательно это сделает.
Нет, вообще нет. Символ это символ. Правила это правила.
Хорошо.
ы.
Вот тебе дан символ. Толку с такого символа без правил?
Что такое толк? Польза? Можно рисовать его на логотипах, например. Или нарезки делать смешные. В общем, применение есть, символ есть, а правил нет.
https://www.youtube.com/watch?v=z2Jd9zS8BnQ
Ок. В математике не так.
Причём тут математика к символу "ы"? Мы говорили о символах
>Символ всегда даётся в совокупности с правилами оперирования им.
Дошли до Ы и пришли к противоречию.
>Ок
Выходит, что символ не всегда даётся в совокупности с правилами оперирования им.
Мы говорим про математику, не про логотипы.
>Причём тут математика к символу "ы"?
Но теперь да, про математику.
>Следует. Символ всегда даётся в совокупности с правилами оперирования им.
Выходит, что символ не всегда даётся в совокупности с правилами оперирования им. Не следует.
>Не следует.
То есть из первого не следует второе.
>Если бы в вузовской математике единица понималась бы как символ, то её изучение повторяло бы изучение единицы в школе.
А другой путь убедиться в этом следующий: предположим, что данное утверждение верно. тогда
>все здания были бы одинаковыми.
Но это не так. Противоречие. Утверждение неверно.
>Если бы это было так, то в вузе бы изучали таблицу умножения
Значит и это утверждение неверно. Значит это не так.
> это символ, который можно писать на бумаге и действия с которым можно производить согласно таблицам сложения и умножения.
Значит это и для университета верно.
Значит единица из школьной математики и из вузовоской математики - это одна очень одинаковая единица.
То есть
>В университете 1 - это элемент множества с некоторой структурой.
это и многое другое будет верно и для школьной единицы и для любой другой единицы, потому что понятия другая единица просто нет. Единица одна и та же везде. Ты улавливаешь мысль?
А значит
>Пересечение школьной математики и высшей математики
Непусто. Как минимум там единица. В качестве упражнения предлагаю тебе взять все понятия школьной математики и проверить, принадлежат ли они множеству вузовской математики.
Это шутка.
В математике - всегда.
Ну допустим, давай так, какие ты можешь производить операции с символом ⊃ ?
Пример правила. Символ ⊃ может стоять только между двух термов.
Это не операция.
Это правило оперирования.
Такого понятия нет. Если хочешь говорить о математике давай говорить о математике.
>В математике - всегда.
Эх, а мне легко давалась метаматематика. Но как это использовать? Ведь это уже никому не нужно.
"В математике каждый символ имеет определённый смысл"
То, что ты хочешь сказать.
Такое понятие есть.
Пруфы, Билли.
>метаматематика
Сложна, сложна, ты к чему?
Гуглить и я умею, у меня эта же ссылка открыта. Не думай, что я об этом не думал. Это речевой оборот, а не строгое понятие.Пруфы, Билли.
Про что угодно можно сказать "это речевой оборот, а не строгое понятие". Ты меня понял, очевидно. Давай дальше.
Нет, есть строгое математическое понятие. А есть речевой оборот. Ты сам решил говорить о математике, так давай говорить о математике. Без пруфов дальше двигаться не получится.
>"В математике каждый символ имеет определённый смысл"
>То, что ты хочешь сказать.
Вот это правда, но это как бы и есть "обозначение", когда ты в символ смысл вкладываешь.
Не мешало бы завести "нытья тред", ну или я по недальновидности своей не нахожу его. Или тогда сразу в /b/ катиться, дабы не мешать умняшам своими быдлопроблемами.
То чувство, когда ничего не понимаешь в математике, потом смотришь на успешную молодежь со всяких матфаков, года на 4 младше, и разумеешь, какой же тупой люмпен по сравнению с ними.
То чувство, когда ничего не понимаешь в математике, потом смотришь на успешную молодежь со всяких матфаков, года на 4 младше, и разумеешь, какой же тупой люмпен по сравнению с ними.
Процитированную тобой фразу написал не я.
Слова "символ всегда даётся в совокупности с правилами оперирования им" тебе понятны, не спорь.
Как ты собрался оперировать операциями? Есть символ, есть правила оперирования, есть само оперирование,обозначается как "+" какой-нибудь. Ну и что делать в таком случае?
>Есть символ
Ну там 1 и 2. Для них верно, то что ты говоришь. А с плюсом как быть? Он сам и означает операцию.
Символ + является просто символом +. Речь строго о синтаксисе.
>символ всегда
То есть твоё "всегда" означает, что это ко всем применимо символам. Да я понимаю, синтаксис, но есть же разница. Есть то, чем оперируют, число, например, для него верно то, что ты сказал. А есть целый класс символов, означающих сами операции, или другие какие-то вещи.
>Символ + является просто символом +
Не просто, у него строго определённый смысл.
Вспомнил: понимаешь разницу между объектом и субъектом? Вот часть символов субъекты и к ним применимо то, что ты сказал. А к части нет. Твоё всегда неверно. Не всегда.
Ну так то, даете книги, нет?
В том что ты ищещь скрытый смысол там ге его нету.
Ну нет так нет. А вдруг есть?
Значит мы все русиш коммишвайне. ШИНЕЛЬ ШВАЙНЕ, ПИТ РУСИШ ФОТОФКА С КАРТОФАНСЧИКОМ!!!
Полностью сводящийся к описанию, какие комбинации с другими символами он может образовывать, какие не может.
Символы, обозначающие операции, являются символами. Символы для обозначения операций ничем принципиально не отличаются от букв латинского алфавита или цифр.
Короче, анон, мне к тян пора бежать, не знаю траливалируешь ты или нет, в любом случае время убили и норм, но если вдруг нет я чего тебе сказать пытался. Нет никакой школьной математики или не школьной. Есть математика. Следующую часть не понять без понимания предыдущей части, но это не отдельные какие-то сущности. Да как и с любой другой наукой, наверное, не слышал, чтобы говорили о школьной биологии и вузовской биологии.
Это противоречит формальному методу.
Много ли биологов ты видел на этой доске? Их вообще мало после лысенковщины. Те, что есть, до сих пор сусликов выращивают вместо науки.
Так к чему ты это, лол? Причём тут коммунизмус? Я говорил о том, что их могли прижать сверху и сказать стране нужны бля паравозы а не ваши гамалогии, а они могли задачки хитрые туда вставлять и прочий подтекст, как итог дохера математиков в совке было годных. Вроде того.
Без понятия, что это. Если ты прошаренный и сильно умнее меня, всякие там Гёдели неполные и прочая, то тогда это бесконечный разговор был бы, нельзя доказать заведомо ложную чушь не прибегая к демагогии.
>Я говорил о том, что их могли прижать сверху и сказать стране нужны бля паравозы а не ваши гамалогии, а они могли задачки хитрые туда вставлять и прочий подтекст, как итог дохера математиков в совке было годных. Вроде того.
Это ты сейчас сказал
>партия сказала "напихайте в учебники картофана с водовкой" а математики такие "не, нихуя" и получились арнольды с колмогоровыми
Так что ли?
Формальный метод провозглашает, что математику можно свести к синтаксису. Не нужно изучать "смысл" значков - достаточно изучить правила комбинирования этих значков друг с другом. Без разницы, означает ли значок сущность или же утверждение о сущностях, - все значки равноправны. Значок + не имеет качественного отличия от значка 1, различаются лишь правила оперирования этими значками.
>а математики такие "есть!", а сами "не, нихуя"
Вроде того.Но
> наверное это имеется ввиду
>Но это неточно.
Я там заблаговременно оставил дисклеймер на случай, если несу полную ахинею.
Я не могу понять, как можно оперировать операцией. Применять или не применять? Да сложно, анон, я ещё слаб для такого.
> как можно оперировать операцией
>Не нужно изучать "смысл" значков
Всё, понял. Тогда это ничем не отличается от рисования кракозябров на песке.
Оперируют символом.
Если кракозябры рисуются по точным правилам - не отличается.
>Анон, в общем есть такая проблема, у меня матан ведет чокнутая старушка, которая уже в маразме и не совсем понимает что происходит вокруг нее. В общем из каждого экзамена, а я сдавал ей в зимнюю сессию, она устраивает какой-то цирк, экзамен начинается в 10 утра, а заканчивается в 9 вечера. Так вот, чтобы получить у нее тройку нужно знать доказательства теорем, а перед этим решить задания (что-то типа допуска к теоретическим вопросам). Сейчас у меня идут ряды, числовые, функциональные, фурье и т.п. и я хотел спросить, есть ли где-нибудь хороший учебник по математике, где хорошо изложены вышесказанные темы?
>
Тер-Крикоров, Шабунин - Курс матана
Будак - кратные интегралы и ряды
В самом учебнике пишут что курс краткий и опускаться в самую суть математики не нужно и вообще зачем, если мы прикладники?
Но тем не менее арнольд как то получился из этой книжки.
Какой смысл в правилах ради правил? Язык нужен для записи мыслей, не наоборот. Это форма ради формы, высшее извращение, возведённое в абсолют. Такая математика мне чужда.
> арнольд как то получился из этой книжки.
Ну мне кажется такое, или похожее, могло происходить.
Формальный метод позволил найти и устранить пробелы у Евклида, остававшиеся незамеченными тысячи лет. Кроме того, он позволил устранить противоречия в теории множеств. Его польза неоспорима.
Может быть.
А может деление на две культуры придумали коньюктурщики которые ящик решить не могут но острые анальные боли из за этого давали о себе знать, вот и получилися учебники для начинающих с уровнем изложения как для доцентов.
Тогда математика нахуй не нужна. Комплюктер уже сейчас может решать все что угодно по формальным правилам совершенно не понимая сути введенного в него.
>устранить пробелы у Евклида
> он позволил устранить противоречия в теории множеств.
На парадоксах держится мироздание. Устранить его значит обменять поиск истины на почёсывание ЧСВ.
И потом, за две единицы, когда суть единицы в том, что она одна, блядь, единица, однаааа. Евклид бы тебе ебало разбил.
https://www.youtube.com/watch?v=Hc5ysppl-pk
Это называется "пруф-ассистант". К сожалению, компьютер не умеет строить формальные теории. Для человека формальные теории не равноценны. Одни ценнее других. Компьютеру эту разницу пока никто не смог объяснить.
Единица как натуральное число, как целое число, как рациональное число, как вещественное число, как комплексное число и как кватернион - это уже шесть разных единиц.
Шесть раз бы набил.
Не соглашусь.
Но он может все что сейчас работать на высочайшем уровне абстракции, до которого бурбаки так и не дошли, оперировать с понятиями совершенно наплевав на их внутреннюю структуру. К этому же ты стремишься в своемизучении математики, или нет?
Компьютер не умеет абстрагироваться. Он не сможет пронаблюдать за коровами, яблоками, камнями и написать формальную теорию на основе своих наблюдений.
Не советую упоминать Бурбаки.
Зачем они ему нужны, если мы работаем с числами с которыми все понятно еще с аксиом пеано?
Он не сможет получать новое математическое знание - предлагать новые формализмы и устанавливать в них нетривиальные изоморфизмы. Его потолок - проверка синтаксической корректности текста и перевод из одной формальной системы в другую.
Сам так решил или кто то сказал? Или ты забыл что ты сам набор логических конструктов ошибочно отождествляемый скелет психики как себя?
>Хм, он упрекал их в том, что они пытаются заглянуть в душу математики, систематизировать, рационализировать душу вместо того, чтобы? Верить? Типа Бурбаки убивают магию математики? Что-то у меня совсем иные представления были о "дедах".
>ты сам набор логических конструктов ошибочно отождествляемый скелет психики как себя
Арнольд был прав.
Нет, дружок, таким конструктом являешься ты. Каждому воздаётся по его вере.
Теперь опровергни что каждое решение в жизни ты выбираешь исходя из прошлого опыта.
Зачем?
Затем что ты пытаешься подебить в споре, а не прийти к истине.
Тебе виднее, дорогой ты мой телепат.
Тебе уже два разных человека про одну и ту же мысль говорит а ты извиваешься как уж на сковородке, как вошь на гребешке, как еот когда пытаешься её обнять, как тригонометрическая функция вокруг оси иксов.
Так. И? Ты что-то хотел?
Хорошо, я придумал. Докажи, что ты не верблюд, тогда и поговорим.
Давай определение верблюда.
Верблюд это то, что ты понимаешь под "верблюд".
Рудин, писал же. Он короткий, есть топология.
>чебники для начинающих с уровнем изложения как для доцентов.
Форма и содержание, анон, форма и содержание. Как говорил какой-то умный дядька:"Если профессор не может объяснить пятилетнему ребёнку чем он занимается, то он ничем не занимается."
Если учёный не может объяснить восьмилетнему мальчику чем он занимается — он шарлатан. Оригинальная фраза: «Если ученый не может объяснить уборщице, которая убирается у него в лаборатории, смысл своей работы, то он сам не понимает, что он делает» — приписывается Резерфорду.
Бамп.
Но ведь это очевидная ерунда.
Дмитрий Каледин опроверг это высказывание, назвав его хуитой.
Тут Калоедин без базара прав.
Не стоит всё так буквально воспринимать.
ОП, добавь список Павлова
=====
Теория множеств:
1 уровень: Н. К. Верещагин, А. Шень: Начала теории множеств.
2 уровень: F. W. Lawvere, S. H. Schanuel: Conceptual Mathematics: A
First Introduction to Categories.
3 уровень: F. W. Lawvere, R. Rosebrugh: Sets for mathematics.
Линейная алгебра:
1 уровень: И. М. Гельфанд: Лекции по линейной алгебре.
2 уровень: М. М. Постников: Лекции по геометрии. Семестр 2: Линейная алгебра.
2 уровень: А. И. Кострикин, Ю. И. Манин: Линейная алгебра и геометрия.
3 уровень: Н. Бурбаки: Алгебра, главы 2 и 3.
Алгебра:
1 уровень: И. Р. Шафаревич: Основные понятия алгебры. (Это обзор, и
читать его надо соответствующим образом.)
1 уровень: Н. А. Вавилов, Конкретная теория колец, Конкретная теория групп — содержат много примеров и занятных комментариев, стиль очень специфический, на любителя.
2 уровень: Э. Б. Винберг: Курс алгебры.
2 уровень: F. Lorenz: Algebra (2 тома).
3 уровень: С. Ленг: Алгебра. (Немного устарела.)
3 уровень: P. Aluffi: Algebra: Chapter 0
Общую топологию, видимо, отдельно учить не стоит, ибо ничего
приличного я не знаю. Можно довольствоваться тем, что уже есть в
других книгах, вроде Рудина и Хелемского.
Впрочем, при надобности можно смотреть книгу Дж. Келли, Общая топология,
главы 1-3 и более поверхностно 5-7, но в последних уже сильно больше
материала, чем надо.
Одномерный вещественный анализ:
1, он же и последний уровень: У. Рудин: Основы математического анализа.
Теория меры:
1 уровень: П. Халмош: Теория меры.
1 уровень: W. Rudin: Real and complex analysis. Первые 8 глав.
Одномерный комплексный анализ:
1, он же и последний уровень: А. Картан: Элементарная теория
аналитических функций одного и нескольких комплексных переменных.
Функциональный анализ:
1 уровень: А. Я. Хелемский: Лекции по функциональному анализу.
1 уровень: А. А. Кириллов, А. Д. Гвишиани: Теоремы и задачи
функционального анализа.
Гладкие многообразия:
1 уровень: Дж. Милнор: Теория Морса.
1 уровень: Дж. Милнор, А. Уоллес: Дифференциальная топология.
2 уровень: Джет Неструев: Гладкие многообразия и наблюдаемые.
3 уровень: J. M. Lee: Introduction to smooth manifolds.
[Между 2 и 3 разница небольшая, можно читать вместе.]
Алгебраическая топология:
1 уровень: A. Hatcher: Algebraic Topology.
2 уровень: P. May: A Concise Course in Algebraic Topology.
2 уровень: Tammo tom Dieck: Algebraic Topology.
Категории: [К сожалению, я не знаю книг с достаточным количеством примеров.]
1 уровень: Тоже, что и 2 уровень теории множеств.
2 уровень: С. Мак Лейн: Категории для работающего математика.
Коммутативная алгебра:
1 уровень: М. Атья, И. Макдональд: Введение в коммутативную алгебру.
http://lj.rossia.org/users/dmitri_pavlov/12706.html?replyto=536226
=====
=====
Теория множеств:
1 уровень: Н. К. Верещагин, А. Шень: Начала теории множеств.
2 уровень: F. W. Lawvere, S. H. Schanuel: Conceptual Mathematics: A
First Introduction to Categories.
3 уровень: F. W. Lawvere, R. Rosebrugh: Sets for mathematics.
Линейная алгебра:
1 уровень: И. М. Гельфанд: Лекции по линейной алгебре.
2 уровень: М. М. Постников: Лекции по геометрии. Семестр 2: Линейная алгебра.
2 уровень: А. И. Кострикин, Ю. И. Манин: Линейная алгебра и геометрия.
3 уровень: Н. Бурбаки: Алгебра, главы 2 и 3.
Алгебра:
1 уровень: И. Р. Шафаревич: Основные понятия алгебры. (Это обзор, и
читать его надо соответствующим образом.)
1 уровень: Н. А. Вавилов, Конкретная теория колец, Конкретная теория групп — содержат много примеров и занятных комментариев, стиль очень специфический, на любителя.
2 уровень: Э. Б. Винберг: Курс алгебры.
2 уровень: F. Lorenz: Algebra (2 тома).
3 уровень: С. Ленг: Алгебра. (Немного устарела.)
3 уровень: P. Aluffi: Algebra: Chapter 0
Общую топологию, видимо, отдельно учить не стоит, ибо ничего
приличного я не знаю. Можно довольствоваться тем, что уже есть в
других книгах, вроде Рудина и Хелемского.
Впрочем, при надобности можно смотреть книгу Дж. Келли, Общая топология,
главы 1-3 и более поверхностно 5-7, но в последних уже сильно больше
материала, чем надо.
Одномерный вещественный анализ:
1, он же и последний уровень: У. Рудин: Основы математического анализа.
Теория меры:
1 уровень: П. Халмош: Теория меры.
1 уровень: W. Rudin: Real and complex analysis. Первые 8 глав.
Одномерный комплексный анализ:
1, он же и последний уровень: А. Картан: Элементарная теория
аналитических функций одного и нескольких комплексных переменных.
Функциональный анализ:
1 уровень: А. Я. Хелемский: Лекции по функциональному анализу.
1 уровень: А. А. Кириллов, А. Д. Гвишиани: Теоремы и задачи
функционального анализа.
Гладкие многообразия:
1 уровень: Дж. Милнор: Теория Морса.
1 уровень: Дж. Милнор, А. Уоллес: Дифференциальная топология.
2 уровень: Джет Неструев: Гладкие многообразия и наблюдаемые.
3 уровень: J. M. Lee: Introduction to smooth manifolds.
[Между 2 и 3 разница небольшая, можно читать вместе.]
Алгебраическая топология:
1 уровень: A. Hatcher: Algebraic Topology.
2 уровень: P. May: A Concise Course in Algebraic Topology.
2 уровень: Tammo tom Dieck: Algebraic Topology.
Категории: [К сожалению, я не знаю книг с достаточным количеством примеров.]
1 уровень: Тоже, что и 2 уровень теории множеств.
2 уровень: С. Мак Лейн: Категории для работающего математика.
Коммутативная алгебра:
1 уровень: М. Атья, И. Макдональд: Введение в коммутативную алгебру.
http://lj.rossia.org/users/dmitri_pavlov/12706.html?replyto=536226
=====
У Стругацких ещё было:
Выбегалло отреагировал немедленно.
— Эта... — сказал он. — так ведь я и говорю, ценное же начинание. Элемент необъяснимого имеется, порыв снизу... почему я и рекомендовал. Эта... — сказал он. — объясни, мон шер, товарищам, что тут у тебя к чему.
Старичок словно взорвался.
— Высочайшее достижение нейтронной мегалоплазмы! — провозгласил он. — ротор поля наподобие дивергенции градуирует себя вдоль спина и там, внутре, обращает материю вопроса в спиритуальные электрические вихри, из коих и возникает синекдоха отвечания...
Часто не очень сведущий, но очень самолюбивый человек прибегает к такому приёму, чтобы нагородить смысловой забор и спрятать за ним собственную некомпетентность. Математика тут не причём, это сплошь и рядом встречается.
Анон выше написал:
>А может деление на две культуры придумали коньюктурщики которые ящик решить не могут но острые анальные боли из за этого давали о себе знать, вот и получилися учебники для начинающих с уровнем изложения как для доцентов.
Это так удачно вписывалось сюда по смыслу, что я не удержался. Конечно, было бы странным считать, что математики идиоты и не могут распознать шарлатанов в их рядах, так что это всё просто художественный ход. Хотя, я склонен думать, что какое-то разумное зерно в этом есть.
Спасибо большое!
А кто это такой?
> Категории: [К сожалению, я не знаю книг с достаточным количеством примеров.]
> 1 уровень: Тоже, что и 2 уровень теории множеств.
> 2 уровень: С. Мак Лейн: Категории для работающего математика.
0. Schanuel, Lawvere: Conceptual mathematics
1. Tom Leinster: Basic category theory
2. Steve Awodey: Category theory
2. Herrlich, Strecker, Adamek: The joy of cats
3. Mac Lane: Categories for working mathematician
God-tier: Leinster: Higher operads, Lourier (не знаю, кому это вообще может понадобиться)
>нумерация с нуля
>теория категорий
Это не нумерация. Мне просто было лень копировать и тем более самому писать слово "уровень". 0 - это кагбе совсем вот граунд-зиро по-моему.
test
Математик из Бёркли.
Тут какие-то частные случаи. Что в моём случае делать?
Там есть твой случай. За тебя решать никто не будет.
Как найти НОД(x; 1-x) при 0<x<1?
В каком кольце?
А?
Китайская комната. Маняматик вроде говорит разумные вещи, но когда просишь его пояснить о чем он он теряется и не может что такое тангенс.
Это я к тому что разобраться действительно ли человек понимает то то знает или нахватался понятий без понимания их сути очень сложно, долго и муторно.
Проверить знает человек математику или нет просто, даешь ему задачку и смотришь может он её решить или нет, а для проверки знает ли он суть гомоморфоного образа из пустого в порожнее нужно самому знать что это и сидеть с ним и разбирать это вот все.
Вот из книжки фейнмана отрывок про знания которые ты якобы знаешь, но на самом деле не знаешь
Потом я был в Инженерном институте на вступительном экзамене. Экзамен был устный, и мне разрешили послушать. Один абитуриент был просто великолепен. Он отлично отвечал на все вопросы.
Его спросили, что такое диамагнетизм. Он ответил совершенно правильно.
Потом его спросили: «Что происходит с лучом света, когда он проходит под определенным углом через слой материала определенной толщины и с определенным показателем преломления?»
— Он выходит, сместившись параллельно самому себе, сэр.
— А на сколько он сместится?
— Я не знаю, сэр, но я могу посчитать.
Он посчитал. Все было прекрасно. Но у меня к этому времени уже были подозрения.
После экзамена я подошел к блестящему молодому человеку и объяснил, что я из Соединенных Штатов и хочу задать несколько вопросов, которые никак не повлияют на результат экзамена.
Для начала я спросил, может ли он привести какой-нибудь пример диамагнетика.
— Нет.
Тогда я сказал: «Представьте себе, что эта книга стеклянная, и я смотрю сквозь нее на что-нибудь на столе. Что случится с изображением, если наклонить стекло?»
— Изображение повернется, сэр, на угол, в 2 раза превышающий угол наклона.
— А вы не путаете с зеркалом?
—Нет, сэр.
Он только что сказал на экзамене, что луч света сместится параллельно самому себе, и, следовательно, изображение сдвинется в сторону, но не будет поворачиваться ни на какой угол. Он даже вычислил, насколько изображение сдвинется, но он не понимал, что кусок стекла — это и есть материал с показателем преломления и что его вычисления имели самое непосредственное отношение к моему вопросу.
Надо ли время от времени перечитывать книги по математике?
МАТЕМАТИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ВСЕЛЕННОЙ ИЗ НИЧЕГО ЧЕРЕЗ РЯДЫ https://youtu.be/JjDTXFL-j0k
Корень квадратный из два плюс корень квадратный из три равны округленно числу Пи! Почему так?
Да,в точности это имел ввиду! Прекрасно помню эту историю, да и вообще Фейнман торт! В некотором роде мой кумир, я вдохновляюсь им ежжи!
Не знаю, но это любопытно.
Сумма первого ряда равна 0, сумма второго -1. Каким местом у него -1=-0?
Это просто лулз. У него логическая ошибка в рассуждении.
Скорее арифметическая,там хоть как бред получается. Лишь бы мозги людям пудрить. А ведь кто-то поверит.
Перейдет ли еще человечество на двенадцатеричную систему счисления вместо десятичной или какую-то другую еще?
Оно использует сразу несколько систем. Сейчас во всю используется шестнадцеричная и двоичная для компов.
Удельное натуральнологарифмическое число кодов (чисел) (плотность записи информации) описывается уравнением y=lnxx, где x — основание системы счисления. Из уравнения следует, что наибольшей плотностью записи информации обладает система счисления с основанием равным основанию натуральных логарифмов, то есть равным числу Эйлера (е=2,71…). Эту задачу решали ещё во времена Непера при выборе основания для логарифмических таблиц. Из целочисленных систем счисления наибольшей плотностью записи информации обладает троичная система счисления.
Я тут начитался всякого, мол теория топосов в теории может иметь самые различные применения. Описывают языки, музыку, кучу всего такого. Это правда? Какие применения могут быть по вашему мнению?
Всё, до меня дошло, это канал с приколами. Он гомункула делал.
Ну, а я о чем
Хотя... Я тут в вики глянул... Написано, что ирл > На самом деле, оба утверждения могут быть точно сформулированны и формально доказаны
https://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D0%BA%D1%82%D0%BE%D1%80%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D0%BA%D0%BE%D0%BB%D1%8C%D1%86%D0%BE
Если это Z кольцо целых чисел, то задача некоретна, поскольку таких x не существует.
Если это Q кольцо рациональных чисел, то задача коректна, раскладываешь числа на простые множители и смотришь пободные.
Если это R, то задача некоректна. Поскольку существует разное разложение на простые множители.
Там что-то вроде биекции получается мысля, если не ошибаюсь.
S = 1-1+1-1+1-1...
S-1 = -1+1-1+1-1+1...
Где каждому 1 из S соответствует один -1 из S-1. Если же помножить S на -1, то каждому -1 из -S будет соответствовать один -1 из S-1, аналогично же и с положительными единичками. Поэтому, наверное, получается, что так
S-1 = -S
Но это больше похоже на софизм. Не очень хорошо получается.
Да там суть в том, что n опускается, вспомни в матане сколько раз из-за n+1,n-1 наёбывался?
Ну типа n тый элемент либо -1 либо 1, от n зависит, вот он с этим играется и получает всякие глупые результаты. В одном случае говорит, что 1 последнее, а потом какого-то хуя n смещает и уже -1 последнее.
Не софизм в общем, а наёбка. Так дела не делаются.
Cпасибо анону посоветовавшему мат. логику.
Разобрался?
Ты про Σn=0(-1)ⁿ?
Ну да. Где-то ошибся хочешь сказать?
Я просто подумал, что с формальной точки зрения тут все хорошо вроде как... Ну, ты же согласен, что Σn=0(-1)n равномощно Σn=0(-1)n+1? Разве нет? По-сути то (-1)Σn=0(-1)n=Σn=0(-1)n+1. Нет?
Σn=0(-1)n равномощно Σn=0(-1)n+1 , но не равно. И Σn=0(-1)n+1 не равно Σn=0(-1)n-1.
Вернее, что я несу, сумма это одно, множество это другое. Короче нет, не согласен. Множества равномощны, суммы их элементов не равны.
Короче, мне эта ерунда ломает сознание. Сами разбирайтесь https://ru.m.wikipedia.org/wiki/Ряд_Гранди
>округленно
Значение знаешь?
https://ru.m.wikipedia.org/wiki/%D0%A7%D0%B5%D0%B7%D0%B0%D1%80%D0%BE%D0%B2%D1%81%D0%BA%D0%BE%D0%B5_%D1%81%D1%80%D0%B5%D0%B4%D0%BD%D0%B5%D0%B5
Вот, смотри. Это не сумма, а сумма по Чезарро. Это не сумма в обычном смысле. Что-то вроде сумма натурального ряда равна -1/12.
Это конечно хорошо, но книжек для начинающих это не даст.
То есть наёбка в подмене понятий.
>Иногда называемый рядом Гранди в честь итальянского математика, философа и священника Луиджи Гвидо Гранди (англ.). В обычном смысле, этот ряд является расходящимся. С другой стороны, его сумма по Чезаро равна 1/2.
Понял. А то я думаю, что за херня.
Ещё у меня к этому вопросы.
1-1+1-1=0; n=4
1-(1-1+1-1)=1-1+1-1+1=1; n=5
(-1)^5=-1
1!=-1
А, наебался. Но всё равно тогда получается n=4, 1=0. Это хрень какая-то.
Наебался ещё раз. С 0 по 3. Блин, я уже сам запутался.
Так, ещё раз:
1-1+1-1=0; n от 0..3 допустим.
1-(1-1+1-1)=1-1+1-1+1=1; n 0..3
0=1 получается. Ну и какого хрена? Если там бесконечность это не значит, что можно произвольное n ставить. Если я в sin(pin/2) в одном месте возьму n=10, а в другом 11 sin(10pi/2), sin(11*pi/2), первое 0, второе -1. Чё теперь тоже приравнять их? Корочое херня это. Не вижу я, как тут "оба утверждения могут быть точно сформулированны и формально доказаны". Второе утверждение неверно попросту.
Вот среднее взять согласен, будет 1/2. Короче, может оно и верно, но я не понимаю почему. Может кто-то из анонов объяснит?
Как тебе объяснить манялогику которая верна только в пределах этой самой манялогики?
Еще спроси почему все тян шлюхи, по мнению битардов.
Проиграл. Ладно, короче, не буду забивать голову. Тем более он монахом был каким-то в средневековье, Коши придэ порядок навидэ.
Кстати, книжек от меня, просто настоятельно рекомендую:
Сканави. Элементарная математика.
Гашков. Современная элементарная алгебра.
Мендельсон. Введение в математическую логику.
Шварц. Анализ (в двух томах).
Львовский. Лекции по математическому анализу. Лекции по комплексному анализу.
Винберг. Курс алгебры.
Варден. Алгебра.
Курош. Курс высшей алгебры. Лекции по общей алгебре. Теория групп.
Ленг. Алгебра.
Виро. Элементарная топология.
Зейферт. Топология.
Милнор. Дифференциальная топология (нач. курс).
Хатчер. Алгебраическая топология.
А физику надо совать? На всякий случай впихну:
Кингсеп. Курс общей физики в двух томах (для техников и физмата).
Феймановские лекции по физике (в десяти томах).
Сивухин: Механика. Термодинамика и молекулярная физика. Электричество. Оптика. Атомная и ядерная физика.
Матвеев: Механика и теория относительности. Молекулярная физика. Электричество и магнетизм. Оптика. Атомная физика.
Накидал говна, кушайте. Ну, не совсем говна.
Понял что проблема именно в незнании "синтаксиса". Буду учить.
Молодец!
Так может оказаться, что высшая математика будет легче для понимания чем школьная (и даже возможно школьная будет легче пониматься через высшую)?
Первое вполне, но далеко не всегда, второе точно.
Что значит высшая математика?
В каком смысле легче?
Элементарная алгебра разве не используется в построении и изложении "высшей математики"? И если да, зачем делить их?
Набор утверждений, входящих в программу Лупанова (утверждена минобром)
Для элементарной алгебры есть "Алгебра" Гельфанда/Шеня, а есть что-нибудь в таком духе для качественного повторения школьной геометрии?
Спасибо.
уже был этот вопрос
минимум 2 раза
ГЕОМЕТРИЯ ШЕНЯ
Выходит, что при возрастании скорости масса движущегося объекта возрастает, но и масса стоящего наблюдателя для движущегося возрастает?
https://www.youtube.com/watch?v=Kf76d5sadmE
https://www.youtube.com/watch?v=Kf76d5sadmE
Посоветуйте какой-то раздел математики, который поможет мне быстро сойти с ума (хотя я и не уверен в наличии последнего).
Ээээ, а какой у тебя уровень-то? Кто-то и с тригонометрии с ума сходит.
Вроде того, что почти дочитал Куранта "Что такое математика" и имею совсем небольшие представления. Тригонометрия мне еще не сворачивает горы.
Посоветуйте книгу, где выводятся "Преобразования Лоренца" с нуля и по пунктам.
математика русов
Тогда и никакого совета нельзя дать. ЧТМ - это уровень 6 класса максимум, а чтоб "сходить с ума" нужно потратить на математику много лет.
во двачую
или православная арифметика
Метаматематика.
>это уровень 6 класса максимум
Ну так уж и шестого.
Прекалькулус тотомаса лучше намного. Поясняют зачем нужны мнимые единицы, тащемта например.
Элементарная алгебра.
идиот
При ем тут достоевский? Мы же про математику.
Тем более преобразования это описание одного и того же понятия но разными способами.
>При ем тут достоевский?
Как ты его!
бамп
Анон-тополог, выручай, жутко туплю.
Сказано следующее: Метрическое пространство компактно тогда и только тогда, когда любая последовательность точек в нём содержит сходящуюся подпоследовательность.
Однако если рассмотреть открытый интервал (a, b) в одномерном евклидовом, то он тоже является метрическим пространством, и в нём любая последовательность точек содержит сходящуюся подпоследовательность. Однако (a, b) компактным не является. В чём тут подвох?
Сказано следующее: Метрическое пространство компактно тогда и только тогда, когда любая последовательность точек в нём содержит сходящуюся подпоследовательность.
Однако если рассмотреть открытый интервал (a, b) в одномерном евклидовом, то он тоже является метрическим пространством, и в нём любая последовательность точек содержит сходящуюся подпоследовательность. Однако (a, b) компактным не является. В чём тут подвох?
Помогите вывести преобразования Лоренца, не получается с t.
Какую сходящуюся подпоследовательность содержит последовательность, сходящаяся к b (в объемлющем пространстве)?
Дело в том, что она должна содержать последовательность, сходящуюся внутри самого метрического пространства.
Можно взять какую-нибудь последовательность точек из (a, b), сходящуюся к b в смысле вещественной прямой. Любая её подпоследовательность тоже будет сходиться к b, т.е. будет сходиться в смысле прямой, но не в смысле интервала.
Он просто не содержит нужный предел. Если рассмотреть его отдельно от прямой, такая последовательность "сходится к дырке" в пространстве, другими словами, сходится в себе, но не сходится.
Понял! Спасибо вам!
Давайте истории восхитительные рассказывать уже.
Аноны, выручайте.
Есть один несобственный интеграл.
(1/((9(x^2))-(9x)+2))dx
Нижний предел 0
Верхний предел 1/3
После нахождения первообразной остается
-1/3(log|3x-1|)+1/3(log|3x-2|)
При подстановке пределов вылезает log|1-1|=log(0), то бишь оно не считается
Затем я беру значение (1/3)-ε, ε=1/6. При подставлении нового верхнего предела получаю 0,195, значит он сходится.
И что далее делать? Тут надо бы применить критерий Коши, но можно ли сравнивать эти два интеграла?
Есть один несобственный интеграл.
(1/((9(x^2))-(9x)+2))dx
Нижний предел 0
Верхний предел 1/3
После нахождения первообразной остается
-1/3(log|3x-1|)+1/3(log|3x-2|)
При подстановке пределов вылезает log|1-1|=log(0), то бишь оно не считается
Затем я беру значение (1/3)-ε, ε=1/6. При подставлении нового верхнего предела получаю 0,195, значит он сходится.
И что далее делать? Тут надо бы применить критерий Коши, но можно ли сравнивать эти два интеграла?
Как же хочется почитать Фихтенгольца.
>Феймановские лекции по физике
Хуйня.
.start crying
Пришел поплакаться.
Пребывая в плену иллюзий о собственной компетенции, сел за чтм куранта и роббинса, и тут же, не сходя с места, соснул в главе о индукции. Вообще алгебру простейшую забыл, все забыл.
crying end
Пришел поплакаться.
Пребывая в плену иллюзий о собственной компетенции, сел за чтм куранта и роббинса, и тут же, не сходя с места, соснул в главе о индукции. Вообще алгебру простейшую забыл, все забыл.
crying end
Пруфируй
>сел за чтм куранта и роббинса, и тут же, не сходя с места, соснул в главе о индукции. Вообще алгебру простейшую забыл, все забыл.
Кто там говорил, что это уровень 6 класса?
Мало того, что шестые классы бывают разные, бывают еще и шестиклассники такие себе. Вот я из этих был, лол.
Ну если говорить о 6 классе какой-нибудь 57 школы, то может быть, да.
Как строго обосновать, что функция при малых приращениях становится линейной? Просто в матанализе это "интуитивно понятно из геометрических соображений" или что-то вроде этой хуйни.
Я такой же, как и ты, а может, вообще тупой. Обычный анон, во время учебы гонявший дотку и наивно считавший, что вот завтра поступлю в место получше и все автоматом станет заебись. Но не стало, конечно же, ведь оснований для заебися не было от слова совсем.
Для таких как я, проебавших школьную математику, есть переизданный в современной орфографии учебник элементарной алгебры Киселева в 2-х маленьких томах. Вот там даже мне все понятно, а в примерах и задачах нет ничего лишнего, выходящего за рамки курса. В школе жутко бесило, что в говнокнижки по АДгебре пихают задания, о которых вообще ничего не сказано, как их решать, и как вообще надо думать, чтобы приблизиться к решению этой хуйни. В общем то, чего крайне не хватало нищуку без репетитора в 7 классе сельской школы, по сравнению с упомянутыми говенными и скудными на разъяснения учебниками в паре с бестолковыми училками.
Есть разумеется более современный курс элементарной алгебры Гельфанда и Шеня, ясно, что её тоже будет не лишним прошерстить параллельно этому или попозже, порешать задачки, для повторения и разумления вещей, которых не было в вышеуказанном курсе.
Разница в том, что хайпящийся некоторыми гражданами товарищ Киселев больше педагог, чем математик, а его курс школьной алгебры шлифовался опытом на протяжении долгого времени, чтобы было понятно даже таким сельским колхозникам и дауничам, как я.
В общем, неважно, что ты в итоге выберешь, мне лично нравится копаться в истории математики и упарываться рассуждениями о том, что элементарные алгебра и геометрия это не просто хрень собачья, которой по приколу мучают в школе, а вполне реальные науки древности, всяких Вавилонов и Египтов, и от этих мыслей повторять их легче и приятнее.
Всякие адепты нму, мнцмо конечно скажут, что ЧТМ Куранта это изи. Ну в принципе так оно и есть, там совсем немного и по верхам, но без определенной тренировки мозга и элементарной привычке к языку математики читать её будет сложно. Вот тут, внезапно, мне очень понравилась маленькая книжка "Основы анализа" Эдмундо Ландау, также адресованная для таких, как я. Там много небольших теорем и доказательств, что лично мне например очень помогает учиться более-менее грамотно рассуждать.
Ещё можно почитать первые главы к любому курсу калькулюса, там кратко и в общих чертах дается то, что называется у буржуев precalculus. Замечу, что некоторые такие главы богаты именно математическими рассуждениями и простыми заданиями по оным, и они дали мне то, чего не давали в школе, пока я был слеп и безынициативен.
Не знаю, зачем я это пишу, просто захотелось об этом поговорить. Все же тред читают не только вундеркинды и пятидесятисемиты, коих упомянули аноны выше.
>мне лично нравится копаться в истории математики и упарываться рассуждениями о том, что элементарные алгебра и геометрия это не просто хрень собачья
Двачую, вообще не хрень. Совсем.
>Не знаю, зачем я это пишу
Чтобы помочь ещё большим нубам, чем ты и я. Всё правильно делаешь. Добра тебе.
А сейчас есть какой-то аналог пифагорейцев и пифагористов? Единственное что нашел, так то, что во всяких квантовых теориях сознания любят выделять типа пространство идей как у Платона, но с натуральными числами. Что-то вроде того, что натуральное число основа мира и с него все строиться, а мозг это приемник этого пространства (ну, тут, я вспоминаю моментальный подсчет и сравнения чисел в мозгу).
И как вообще с религиозностью и верованиями у математиков?
И как вообще с религиозностью и верованиями у математиков?
Сейчас много псевдоговна, любое такое сообщество с большой долей вероятности антинаучная хуета. Если ты ищешь чего-то эдакого, то бери гугл и гугли отдельные работы или заметки, рассуждения математиков древности, средних веков, современности и выстраивай собственную (религиозную?) систему.
А вообще также, как и у всех остальных. Эти вещи никак не связаны. Среди математиков полно атеистов, буддистов, христиан, индуистов. Тот же Рамануджан формулы у Иштар выпрашивал, например.
Он начинает дрочить сразу квантовую механику с теорией относительности, хотя уже тогда было видно и ясно что они конфликтуют друг с другом, что означает что они либо ошибочны либо не доработаны. Плюс, такая глубокая физика нахуй не нужна для того чтобы посчитать ящик и сколько энергии нужно чтобы забить гвоздь.
Короче, пруфировал тебе в пищевод.
>Иштар
Вот это я наврал, конечно. Это вообще шумерская богиня, лол. Уже всё перемешалось в голове.
>Сам Рамануджан говорил, что формулы ему во сне внушает богиня Намагири Тхайяр (англ.) (Махалакшми) (хинди नामगिरी), почитаемая в Намаккале (там. நாமக்கல்).[
>что означает что они либо ошибочны либо не доработаны.
Не означает же. С чего ты взял?
>оват
кривые на бесконечно малых расстояниях становятся прямыми.
Плюс там же доказательство в арифметическом виде есть, если задан эпсилон переменной, то нужно на основании этого числа задать дельту для значения функции, чтобы числа были меньше дельты и эпсилона.
Теория относительности запрещает перемещение быстрее света, квантовая механика имеет в себе квантовую телепортация ко-ко-ко ничаво ни пириносится, смена спина/импульса/энергии/вектора движения квантово запутанной частицы по воле ктулху происходит
Дальше, по ото гравитация должна квантоваться и существовать гравитационные волны, но при этом элементарные частицы подчинятся силе тяжести так же само как и яблоки с ананасами, что говорит о том что квантования или нету или оно должно быть охуительно маленьким, ведь даже свет притягивается звездами.
>Маа Махалакшми – Богиня богатства, успеха, процветания (как материального, так и духовного), мудрости, плодородия.
>Иштар[1] (аккад. dIštar, логографика: dINANNA, d30) — центральное женское божество аккадской мифологии, богиня плодородия и плотской любви
>Махалакшми-врата — один из священных дней индуизма, в которой замужние женщины-индуски проводят пуджу богине удачи, счастья и процветания Лакшми, ища её благословений на обретение материальных богатств и благосостояния членов семьи. День Махалакшми-враты определяется в соответствии с индуистским лунным календарём, согласно которому он выпадает на пятницу перед полнолунием месяца шравана (июль — август по григорианскому календарю).
>Ворота Иштар — восьмые ворота внутреннего города в Вавилоне. Построены в 575 г. до н. э. по приказу царя Навуходоносора в северной части города.
Максимум кек, вот так опечаточка. Мб я и не опечатался вовсе.
Ньютоновская механика и теория относительности тоже противоречат друг другу, но это не мешает им быть верными, у них разные области приложения, то что верно для макромира неверно для микромира, и наоборот. С чего ты взял, что утверждение про скорость света будет верно для разъединённых квантово запутанных частиц?
Вроде бы недавно была какая-то инфа по гравитационным волнам
>О первом прямом детектировании гравитационных волн коллаборациями LIGO и VIRGO было объявлено 11 февраля 2016 года[3]. Результаты опубликованы в журнале Physical Review Letters[1] и ряде последующих статей.
>Существование гравитационных волн впервые было предсказано в 1916 году[5][6] Альбертом Эйнштейном на основании общей теории относительности[7]. Эти волны представляют собой рябь пространства, распространяющуюся во времени со скоростью света: при прохождении гравитационной волны между двумя свободно падающими телами расстояние между ними изменяется. Относительное изменение этого расстояния служит мерой амплитуды волны[8].
Научные результаты[править | править вики-текст]
Открытие привело к следующим новым научным результатам[26][44][45]:
Прямое обнаружение гравитационных волн.
Прямое доказательство поперечности гравитационных волн[46].
Открытие нового способа наблюдения за Вселенной (гравитационно-волновая астрономия).
Объяснение проблемы гравитационного дальнодействия.
Прямое доказательство существования чёрных дыр.
Прямое доказательство существования двойных чёрных дыр.
Доказательство правильности геометрического подхода к гравитации, на котором базируется ОТО[47].
Обнаружение самой тяжелой из когда-либо наблюдавшихся чёрных дыр звёздных масс.
Установлен верхний предел массы гравитона (10−55 грамм)[48][32].
Кроме того, открытие гравитационных волн не опровергает никаких рабочих версий теории гравитации[49].
Спасибо, аноний, Киселева потом Шеня обязательно проштудирую. На прекалькулюс Стюарта вот поглядывал еще
А насчет линейности что? Может же быть и такая функция, которая не линейна ни на каком промежутке. Может же быть такое?
Я это к тому, что и ОТО и квантовой механике находится всё больше подтверждений. Обе теории скорее всего верны, я не вижу тут противоречий.
Может быть. В любом случае, упоминание имени Богини в треде это знак, что стоит перестать скроллить и дочитать главу учебника.
Мне не нравится такая шизофрения от слова совсем. Нет, конечно, пусть каждый дрочит, на что хочет, но я лучше почитаю нормальную историческую или художественную книжку, чем это мракобесие в духе постмодерна.
>Ньютоновская механика и теория относительности тоже противоречат друг другу
Хуй там стоял.
ОТО это допиленная версия ньютона для охуительных масс.
Нихуя там не нашли, очередные вбросы от журнализдов уровня "ученые сказала, а журналюхи написал ОТКРЫТИЕ ВЕКА!!!!"
Еще ведро сюда принеси и скажи что оно не работает. И это не реактор пахомова-росососси, у него чертежи по всему интернету валяются.
Нет, ибо читай выше и плюс большие аттракторы, стены слоуна, сверхпустоты эридана, черные дыры, воиды между галактиками, гроб гроб кладбище применение теории о дрейфе перигелия меркурия на все подряд
>всяких квантовых теориях сознания
>шизофрения
Вот-вот. Антинаучная хуета.
> что стоит перестать скроллить и дочитать главу учебника.
Действительно. Тоже пойду.
>Нихуя там не нашли
Врёти? Ну как знаешь, дело твоё.
Я нихуя не понял из того, что ты сказал. Спорить не хочу, потому что я не физик.
>Хуй там стоял.
В Ньютоновской механике скорости аддитивны. Скорость света не аддитивна. Противоречие? Противоречие.
>Врёти?
Эфир тоже вроде как открыли. Только намеряли чего то там в три раза больше чем нужно.
Тут так же, вроде чего то намеряли, а что намеряли и почему нихуя не понятно. Получится небось такая же ерунда как с сверхсветовым нейтрино, которое случилось из за того что хуево шнур в пекарню ткнули и получился пинг сколько то там микросекунд.
Есть, это Церковь Чисел. Я ее придумал, когда сидел в битардск тредах. Правда есть большой недостаток в ней, я там единственный участник
Нет, изменяется частота которая тут выступает заместо скорости.
То же самое со звуком, доплер например.
Не знаю, я много всякой хуеты читал по этому эксперименту, ещё до того, как произошло открытие, лет за пять, и мне казалось убедительным всё это. Даже вспомнил где читал, у Пенроуза, ща отрою цитату, там прям эксперимент описывается.
Скорость света не обладает аддитивностью. Скорость в ньютоновской механие обладает. И то и то скорость, из-за этого много срача было поначалу и Эйнштейна хуесосили. А потом смирились. Почему тут также быть не может?
Оно тебе надо? Вся математика - это и так сплошная схоластика.
Я бы не выбрасывал из внимания геометрию хотя бы потому, что она неплохо так подкрепляет интуицию и дает множество наглядных примеров и эмпирических подтверждений простых математических теорем.
Просто её уже обсуждали выше, да у тех же авторов есть книжки и по геометрии. Читай - обчитаешься. Было бы желание.
Недавно вот глянул одну книжку господина Дьедонне "Линеная алгебра и элементарная геометрия", сам не знаю зачем, видно, привлекла небезызвестная фамилия. Так вот, во введении этот товарищ то ли тонко троллит, то ли я вообще не знаю, что все это значит, но он открытым текстом предлагает выбросить известную нам евклидову геометрию с наглядными примерами из школьного курса, утверждая, что все это на изичах решается методами линейной алгебры. И без единого чертежа.
Однако мозги у обычного человека попросту расплавятся от такой геометрии, ибо ценность и смысл той предельно выхолощенной алгебры по отношению к действительности очевидны, как рукав, пришитый к пизде.
Да я и не выбрасывал, думал после алгебры Адамара начать, хз правда хорош он или плох. А тред выше не читывал, но теперь прочту чего там по геометрии упоминается
А алгебру можно решать с помощью геометрии?
Последний раз когда я читал про детекторы гравитационных волн самый многообещающй проэкт описывалс примерно так.
Они собирались запустить три спутника в космос с лазорами, сделать из них равносторонний треугольник с длинной ребра 3n километра в котором лазорные лучи будут играть роль ребер, обвешать спутники передатчиками для точного позиционирования, сделать еще на земле/космосе/аллахе сеть передатчиков для еще более точного позиционирования, и сверху еще нацепить на спутники систему взаимосвязи чтобы спутники отправляли друг другу и сети передатчиков тайминги времени когда лазорный луч отправился от одного спутника и когда пришел к другом спутнику.
А тут намеряли что то в лаборатории на земле еще и на 80 метрах.
Так суть в том, что произошло естественное событие, моделью которого должен был быть такой эксперимент, повезло типа, осталось только снять показания.
Звук тоже не обладает аддитивностью. Ультразвук распространяется с такой же скоростью как и инфразвук.
Если ты будешь ехать на машине к сирене звук будет выше, а если от сирены то ниже.
Ту так быть не может потому что колебания. Колебания не могут стать быстрее или медленнее в смысле скорости, у них только может меняться частота амплитуда и прочее.
Странный вопрос. Алгебра и геометрия в общих смыслах идут рука об руку в том числе и в современной математике, со всякими изощренными топологиями и прочим, но я до этого лвла не дошел.
Где-то геометрическое решение/истолкование вполне очевидно и просто, где-то может быть иначе, удобнее рассуждать аналитически, чем пытаться вообразить НЕХ.
Ну да. Свет это колебания пространства, тока не бей, это мой манядомысел.
Я к тому, что пиздели на Эйнштена сильно с такими вот аргументами. А оказалось зря пиздели. Казалось бы да, скорость и там скорость, тут аддитивна а там нет, но может оказаться что противоречия нет на самом деле. Так и в твоём случае с ОТО и квантмехом. А может и нет,сука, я не физик, я физику на уровне двух курсов МухГУ знаю и по книжкам типа той, что скинул. Отстань, короче.
Я не понимаю... Ты ведь, как я понимаю, математик? Почему некоторые математики так плохо знают физику? А если точнее, вообще не знают.
Эксперимент уровня "поставим БАЛЬШОЕ" зеркало между европой и африкой чтобы проверить отодвигаются ли континенты друг от друга или нет."
Это я к тому что масштаб сильно маленький. Чтобы бозон хиггса открыть пришлось коллайдер строить на 30 километров и гонять по нему протоны по кругу под сабатон пару лет, а тут за джва дня буквально после постройки из говна и палочек уже все зафиксировали, получили премию и открыли шампсик.
Я любопытный двачер, по образованию геолог. На парах пинал хуи. Что-то я знаю и готов спорить с тобой, чего-то я практически не знаю и спорить об этом не готов.
>Свет это колебания пространства
Может, а может и нет.
Непроверяемо, пока, из за того что мы пространство померить не можем из за того что все наши инструменты в самом пространстве. Пытаемся померить линейку этой же линейкой другими словами.
Да блядь там две чёрные дыры столкнулись. Представился шанс и измерили.
Ну понятно, да. Аналогия с линейкой охуенная.
>где то там, в далеком и неизведанном угольном мешке пернул шуршунчик. У меня в этот момент стрелка двачехаркачеметра немного дернулась. Это значит что БОХ ЕСТЬ!!!! ПОКАЙСЯ!! ПОКАЙСЯ ИБО ГРЯДЕТ!!!!!!!
Нашёл всё правду про лживого Лоренца и его "преобразвоания", что скажете?
первое сообщение
http://www.e-science.ru/node/105300
первое сообщение
http://www.e-science.ru/node/105300
Обосрался. Ну да, ну а что ты предлагаешь? Шуршунчик, лол.
Повторить эксперимент в большем масштабе, так как я описал, со спутниками и сетками. Ведь так у нас будет большая чувствительность и можно будет действительно зафиксировать пердеж шуршунчика, как перемещение масс материи.
>Повторить эксперимент в большем масштабе, так как я описал, со спутниками и сетками.
Проблема в том, что эти большие масштабы должны быть чуть ли не размером в галактику.
Да, точно оно. Рассказывает о подробностях эксперимента, как его делали и тд.
А он сам разработчик зеркала был вроде.
Вот пусть он тебе расскажет, один хер я своими словами пытаюсь пересказать то, что когда-то, когда ещё телевизор смотрел видел и содержание книжек. Типа моё доверие к эксперименту 2016 году и результатам на этом основано.
Нет, чем больше масштаб тем больше точность.
Вот нам нужны метровые доски с точностью, чтобы каждая доска не больше/меньше чем на скажем один миллиметр отличалась от метра.
Берем значит таких досок метр/миллиметр=1000 доско и ставим их друг к другу в ряд. Меряем расстояние которые они занимают. Если отличается расстояние от километра делим избыток/недостаток на количество досок и узнаем сколько нам еще нужно отрезать/приклеить к каждой доске.
Тут все так же примерно.
Так почему нет, если я о том же говорю? Нужен масштаб в галактику. Тогда да, будешь удовлетворён экспериментом. Попали, анон, то видео, там рассказывается и об этом, ну про галактику, и о том, как можно его на Земле провести и о многом другом. Не смотри, что там Гордон. Тогда ещё тв можно было смотреть, тогда ещё к нему в ночную программу ходили интересные люди.
Скорость света поднимать будешь? Пока из одно конца галактики свет дойдет до другого экспериментаторы скопытятся. Так что треугольники в 30-3000 км это самый простой из необходимых вариантов.
Я мог наврать про галактику, я помню, что большие масштабы и в блишайшие годы сделать это невозможно будет, я это 14 лет назад смотрел, запарил ты.
Анон, ну не хочу я спорить о том, в чём не разбираюсь. Я тебе всё скинул, я тебе как испорченный телефон пересказываю всё это. Просто на этой информации основывается моё доверие к недавнему открытию. Ознакомься и может поменяешь своё мнение. А может и не поменяешь.
Я до сих пор не нашёл ни одного вменяемого вывода "Преобразований Лоренца" с нуля, от сих, до сих, с объяснениями и рисунками. Без академической шизофрении, без пропусков логических ходов итд.
Просто дегенераты какие-то кругом, совок тупой, бля.
Зато нашёл кучу проблем и свидетельств того, что "Преобразования Лоренца" - фуфло чистое.
Просто дегенераты какие-то кругом, совок тупой, бля.
Зато нашёл кучу проблем и свидетельств того, что "Преобразования Лоренца" - фуфло чистое.
Попроси откровения у своей богини. Той, которая с сосульками за спиной, нутыпонел
Восполняй логические ходы сам, выводи формулы, доказывай теоремы, рисуй геометрические интерпретации, обращайся в случае чего к другим книгам или к помощи профессионалов. Это конечно может раздражать, но в учебных целях весьма полезно, так как стимулирует мышление обучающегося и дает понять одну простую вещь - никто не будет лично тебя тащить к знаниям и подгонять все курсы под одного человека. Добывай все сам. У мудрецов древности и вплоть до bleeding-edge моченых современности тоже не было книжек с картинками по интересующей их области.
нет, ты
У меня одна жизнь.
И мне нужно официальное, а не то, что я сам выведу.
Сейчас вот пересмотрел то видео и возник вопрос:"Случаи сталкивания чёрных дыр достоверно известны. А известны ли случаи раздвоения чёрных дыр?" Есть же физическая доска какая-то? Просто когда он заговорил про геометрию, когда процитировал учёного, который сказал, что внутри чёрной дыры нет ничего, кроме пространства-времени, что типа хоть точек на самом деле нет, но можно так рассуждать будто есть некий геометрический каркас, который колеблется и получаются волны разных частот, которые мы называет свет, звук, пук,и так далее, тип геометрический подход вполне допустим, то я сразу вспомнил этот видос(там ссылка по времени). Фигура сначала появляется, точки множатся, она полностью раскрывается, а затем идёт обратный процесс схлопывания. Если нет ни одного случая, когда дыры бы делились, то это на забавные мысли наводит. Короче, с вопросом в кавычках мне куда? В /fiz/ физкультура какая-то?
https://youtu.be/rG6aIVGquOg?t=465
https://youtu.be/rG6aIVGquOg?t=465
Вы занимаетесь лично какими-то либо вычислениями или даже стараетесь самые простые поручить компьютеру?
/sci
Сам вывел, сходил к нотариусу. Куда официальней?
У меня не выводится, мне не понятно хотя бы откуда берутся те идиотские коэффициенты, на которые мы умножаем и почему они именно такие?
Чем |a + a1| отличается от |a| + |a1|?
Подставь a=-a1
Всем 3-3=0, 3+3=6.
>математика
>ото, чёрные дыры
Пиздуйте в свой загон, ушлёпки.
>ото, чёрные дыры
Пиздуйте в свой загон, ушлёпки.
да, действительно полный пидор, я вот с Преобразованиями Лорценца и СТО разбираюсь.
Мне там говорят
>Чо? Дыра в пространстве может делится?
Тоже, считай, слияние, потому и интересно стало.
> Короче, с вопросом в кавычках мне куда?
Ты читать умеешь или только агриться на пустом месте способен?
и человек со звездой сольётся? Он же практически полностью из воды состоит, если сжеть, остаётся совсем ненмого пепла.
у тебя тоже есть сестра с кошачьими ушками, у которой ты хотел бы ковыряться в пизде пальцами?
>звездой
А не факт, что это бывшие звёзды, в том и прикол.
Различают четыре сценария образования чёрных дыр:
два реалистичных
гравитационный коллапс (сжатие) достаточно массивной звезды;
коллапс центральной части галактики или протогалактического газа;
и два гипотетических
формирование чёрных дыр сразу после Большого Взрыва (первичные чёрные дыры);
возникновение в ядерных реакциях высоких энергий.
Не зря Платон писал:"Не знающему геометрии вход воспрещён"
Для начала мы должны определиться в каком агрегатном состоянии находится человек в момент слияния, либо столкновения.
При подлёте к звезе, он испарятеся, получется небольшое газовое облко с частицами микропыли. Верно?
Над Звездой газ, газ сливается с газом, теорема доказана.
При подлёте к звезе, он испарятеся, получется небольшое газовое облко с частицами микропыли. Верно?
Над Звездой газ, газ сливается с газом, теорема доказана.
>"Не знающему геометрии вход воспрещён"
И "Оставь надежду всяк вюда входящий", дада читали это всё в своё время, знаем, масоны, все дела.
Тож думаю, а куда делись старые чёрные дыры, ну были же Мегазвёзды, странно, что обошлось без дыр, не считая чд в центрах галлактик.
Так и над чёрной дырой газ, да пыль. А два газо-пылевых облака должны слиться.
Вот-вот, почему бы им не быть просто точками, максимальная кривизна в них и всё. Тот учёный говорил, что такой подход вполне допустим. А другой его друг говорил, что внутри чд нет ничего, кроме пространства-времени. То есть кроме некоторой геометрии.
https://www.youtube.com/watch?v=rG6aIVGquOg&feature=youtu.be&t=465
Вот представь, что есть многомерное нечто, которое проходит через наш трёхмерный мир, вызывая в нём колебания разной частоты, гравитацию, свет, звук. Оно сначала раскрылось, а теперь схлопывается, дыры сливаются.
https://www.youtube.com/watch?v=rG6aIVGquOg&feature=youtu.be&t=465
Что-то вроде этого представил и захотел спросить, вдруг были случаи деления дыр, лол. Но не было их, да и это по всем канонам было бы странно, два массивных объекта не должны отталкиваться. Короче, пища для размышлений.
В сци я, кстати, больше не пойду, они там эфир обсуждают.
Открывай только не тут, а на ютубе, а то ссылка на время сбивается почему то.
>а теперь схлопывается
Вернее это мы так воспринимаем, на деле же просто двигается дальше, типа если бы мы были двумерными и через нашу плоскость пропускали 3д фигуры. Так и тут, только фигуры большей размерности.
Логическая сумма = объединение множества = дизъюнкция,
логическое умножение = пересечение множества = конъюнкция.
Верно? Или не совсем?
логическое умножение = пересечение множества = конъюнкция.
Верно? Или не совсем?
Сумма это объединение плюс пересечение.
>логическая сумма
>логическая
А, и первое тоже правда.
Но ведь закон сохранения энергии не работает, свет - электромагнитная волна исчезает пройдя большое расстояние.
Рассеивается энергия и всё, нет её. Так что если этот путь запихать в закрытую систему, тут закон сохр энергии уже не работает.
Рассеивается энергия и всё, нет её. Так что если этот путь запихать в закрытую систему, тут закон сохр энергии уже не работает.
Всё, что существует имеет массу. Даже ваши фантази имеют массу.
Как раз квантовая гравитация и должна дать ответ на то, почему информация в чёрной дыре исчезает.
Нихуя там не исчезает. Если бы что то исчезало то проделав противоположный процесс можно было бы получить новую энергию из нихуя.
Съебите нахуй, черти ебаные, итак все засралили своей гавнофизикой.
Вообще, всё это к чему
>Феймановские лекции по физике
>Хуйня.
Не хуйня. Фейнман торт. Я всё.
Допустим свету (электромагнитной волне) для прохождения расстояния, т.е. для движения нужно затрачивать энергию, что звучит вполне логично. Тогда рассивание света (исчезающая энергия вникуда) уже объясняется.
Съеби на хуй, тварына, никому твоя залупа, где пучков нет, не интересна.
Энергия света поглощается при столкновении с материей.
А нечего говорить, что лекции Фейнмана хуйня! Сказал? Пруфируй!
>явление, которое должно происходить
Значение знаешь?
>если она действительно подчиняется термодинамическому описанию, предложенному Стивеном Хокингом.
>В этой ситуации становится очевидным следующий парадокс. Если мы рассмотрим падения в чёрную дыру и последующее испарение для квантовой системы, находящейся в каком-либо чистом состоянии, то — поскольку чёрная дыра в результате не изменилась — получим преобразование исходного чистого состояния в «тепловое» (смешанное) состояние. Такое преобразование неунитарно, а вся квантовая механика строится на унитарных преобразованиях. Таким образом, эта ситуация противоречит исходным постулатам квантовой механики.
>Разрешение этого противоречия — необходимый шаг на пути построения квантовой гравитации.
Знаю.
Пиздишь, не было такого. Пост давай сюда.
И вообще, определения информации нормального нету. Так что некоректно искать то что мы не можем определить.
>бляя, пацаны, у нас уравнения не сходятся, вся вселенная должна сейчас же уничтожится
>определение информации
Их даже несколько. Любое выбирай. Да, это не математика, что поделать.
Кто тебе сказал, что она должна уничтожиться? Нахуй ты додумываешь?
В любом случае все сводится к энергии.
Энергия неуничтожима.
То что в квантовой механике энергия может проебыватся проблемы исключительно квантовиков и нормальных физиков не колышут.
Даже отвечать тебе не хочу, чмо. Игнорирую.
Пизда треду причем уже давно, но я надеялся что не всё так плохо, нахуй эту доску.
треду не пизда
моча проснется - забанит, почистит надеюсь
>В любом случае все сводится к энергии.
>Энергия неуничтожима.
Если не сохраняется информация, то не сохраняется и энергия.
>Закон сохр энергии прочитай, а не дебилов всяких.
>То что в квантовой механике
>нормальных физиков
Нет нормальных и не нормальных физиков. Есть физика и её разделы. Как нет высшей и школьной математики. Есть нормальные физики, а есть Катющик.
Ясно. Математик не смог в доказательство. Зато словами бросаться смог. Иди пучки считай.
>ЧТМ - это уровень 6 класса максимум
Серьезно?
В предыдущий раз тебя предупредили, теперь будет бан за говнофорс в прикрепленной теме.
>Есть нормальные физики, а есть Катющик.
Есть физики, а есть Катющик.Есть математики, а есть пучкисты.
фикс
Это не говнофорс, а вполне соотвествующая реалиям треда сатира. Неужели тебе нравится засилия таких вот людей, которые кричат - ТУТ НЕТ ПУЧКОВ ОЛОЛОЛО.
Он безусловно долбоеб. Но не больший, чем ты.
Мем про пучкиста никому не понравился, ты просто засрал доску идиотскими шутками. Даже сиплоглота забыли.
Я всегда просто репортил и скрывал твои посты, ты не создаешь годного контента, ты только срешь.
>Мем про пучкиста никому не понравился
Мне понравился. Чрезвычайно ёмко и точно.
>>153580-кун
>Он безусловно долбоеб. Но не больший, чем ты.
И почему ты так считаешь? Я надеюсь, посты "ТУТ НЕТ ПУЧКОВ НИ МАТЕМАТИКА", ты тоже скрываешь?
>Даже сиплоглота забыли.
Я не имею к ниму никого отношения. Я бы не стал создавать настолько некачественный мем.
>некачественный
Спорно. На мой взгляд очень ёмко описывает вот таких людей.
таких Вот потому и ёмко, не хочу простыню писать и ещё больше мусорить.
Я не понимаю, каких. Напиши пасту, раз уже начал шитпостить.
Я не шитпостил, я пытался понять, почему человек так отзывается о лекциях Фейнмана. То, во что это вылилось мне не нравится и дальше мусорить я не хочу.
Суть Бытия
Из-за маленькой массы носителей, энергии на движение электромагнитной волны тратится немного, но всё-таки она через время кончается и свет исчезает, рассеивается.
Но имеющиеся сегодня формулы и законы не позволят нам найти эти велечины.
Зато, в принципе, можно собрать статистики, от каких галактик свет доходит, а от каких нет, и взять растояния до них.
Мы узнаем на какой путь у света хватает энергии распространения.
В зависимости от показателей света количество энергии будет варьироваться, это нужно учесть.
Тоже самое можно говорить и о гаммаизлучении, звуке, гравитационных волнах и всём остальном.
Да, в идеальном случае нет сил трения, хуё-моё, и любой объект должен лететь бесконечно в такой системе. Но волна - не прямолинейно летящий объект, волне нужно самовоспроизводиться, вот на это и уходит энергия - на волнение. Само волновое движение отнимает энергию.
Волна затухает, т.к. пропадает энергия, проверьте на кружке с водой.
А квантовая физика - вообще говно, забудьте. Типа у каждого объекта есть соответствующая волна, идиот, слов нет. У движущейся машины свои свойства, у электромагнитной волны - свои. Вот и всё, бля.
А в среде, свет аналогично - идёт, идёт, чпок, эта энергия для самовоспроизводства кончилась и дальше он не идёт. Без энергии распространения электромагнитная волна не существует, либо скрывается из поля зрения и застывает до полного развала на кратчайшее мгновение.
В среде и скорость распространения замедляется, но при выходе из объекта, скорость распространения вновь возвращается в первоначальное состояние, т.к. у света есть "память". Но энергии распространения уже мало. Теряется и остальная энергия.
Между атомами свет прыгает со световой скоростью в среде и как только исчезает барьер, свет "вспоминает" кто он и уже херачит на полную.
На огибание объектов энергия распространения опять же расходуется.
Да, полностью и поэтому мы не видим себя в зеркале.
ты про пылинки и прочий мусор на пути света?
это несущественно
Нет, не полностью и поэтому мы видим себя в зеркале.
Нет, я про то, что энергия света поглощается при столкновении с материей.
>Поглощение электромагнитного излучения — процесс потери энергии потоком электромагнитного излучения вследствие взаимодействия с веществом.
Тогда я не понял, зачем ты защищаешь точку зрения, на которую я отвел своими картинками с пучкистами и делаешь мне замечание по поводу картинок.
Звезда огромна и хуярит свет постоянно, забуть про костический мусор на пути света.
Я, ващето, не пучкист. Про пучки я написал затем, чтобы указать, что для мат. треда лекции по физике имеют около-нулевую ценность и не нужно их здесь восхвалять и вообще тащить это сюда, обсуждать.
За последние несколько тредов для начинающих я помню только 1 вменяемый вопрос - что-то там про перестановки. Остальное - что мне прочитать чтобы прочитать учебник по физике/программированию, вопросы из вступительной математики, как представить себе четыреДЭ и прочее. И всё это разрастается на десятки постов с ссылками на википедию или на науч-поп видосы с ютуба.
>что для мат. треда лекции по физике имеют около-нулевую ценность и не нужно их здесь восхвалять и вообще тащить это сюда, обсуждать.
Обязательно было для этого из целого списка хорошей или нет литературы для новичка выделить лекции Фейнмана и устроить срач на 200 постов?
Раз тут такие восхитительные истории по физике, то спрошу.
Как бы воспринималась бы геометрия, если бы вместо "фотографии" подавалась бы голограмма и строилось бы поверх голограммы уже все представления, в том числе и не отраженные реальным миром?
Как бы воспринималась бы геометрия, если бы вместо "фотографии" подавалась бы голограмма и строилось бы поверх голограммы уже все представления, в том числе и не отраженные реальным миром?
И ты вместо своего недовольства высказал подъёбку про пучки? Ладно, раз уж я запостил ПУЧКистов, то запощу качественный пост. Как доказать непрерывность в (i)? Я понимаю, что надо сделать какую-то оценку для нормы, но не знаю, какую именно.
Или в человека уже почти что голографическое зрение, а я выгляжу глупо?
Видимо, "хуйня" потому что, согласно летописям, мистер Фейнман сам был не в восторге от выхолощенной абстрактной математики, слишком, с его возможной точки зрения, оторванной от физической реальности. Но я могу быть не прав.
Анон, я честно попытался представить то, о чём ты говоришь, и соснул. Не знаю, вроде не выглядишь.
Это, несомненно, весомый аргумент, чтобы так отзываться о его лекциях по физике.
Дело в том, что можно было бы, конечно, пройти мимо, но тред для новичков и висит на самом видном месте. Прочитав такой пост новичок скорее всего поверит на слово.
Ну это просто предположение. Может, у кого-то обычная человеческая обида. Всякое может быть.
Но так-то его лекции, разумеется, содержат математические выкладки. Просто полный смысл выражения "X хуйня яскозал" мне видится, как попытка самоутверждения молодого человека, не старше 25 лет.
Я полагаю, что это верное предположение. Но всё дело в том, что Фейнман физик, притом блестящий, он мог что угодно думать о чистой математике, но на его труды по физике и на качество и понятность изложения это никак не повлияло, как не должно влиять и на оценку его трудов по физике. Со второй частью я полностью согласен, мне тоже всё видится именно в таком свете, поэтому и потому, что тред читает много новичков таких "математиков" нужно призывать к ответу.
Может. Называется недиффиренцируемая. Производной у неё не будет.
Потому что физики АБСОЛЮТНО не знают математику. Физиков математика, мягко говоря, не ебёт. А точнее - ебали они математическую строгость пиздоблядским хуйпроёбищем в сраку двести раз, и ссали в дырку.
Так он спрашивал почему математик не знает физику.
Ааа, я понял.
Охуительных историй тред.
Ну ебана, в прошлом треде разбирали же.
Физика это абстракция реальных вещей у которых усилены нужные и убраны ненужные нам свойства в какой то конкретной задаче.
Математика это совсем оторванная от реальности хуита, у которой даже нету примерного образа понятия количества три дома, три кирпича, три пепяки, три разуплотнения.
Но из за того что она полностью оторвана и замкнута на саму себя ею удобно исследовать другие науки.
А некоторые начинают считать что математика это и есть физика. Вон выше по треду писалось что в черной дыре информация пропадает, физика нироботоет((, а по факту в черную дырень все проебывается без проблем, ничего никуда не пропадает.
Может, называется фрактал. На практике встречается только у цветной капусты.
Бамп интересной задаче.
Нет. Я попросил аргументировать и найти мне число три в реальной жизни а мне про углы комнат начали рассказывать.
Архивач треда: http://arhivach.org/thread/254519/
Если кто-то хочет продолжить обсуждение физики на этой доске, то ему необходимо создать для этого отдельный тред.
Если кто-то хочет продолжить обсуждение физики на этой доске, то ему необходимо создать для этого отдельный тред.
Тред для общематематических разговоров и вопросов о философии математики: https://2ch.hk/math/res/10487.html
А как доказать именно то, что функция на маленьких промежутках становится линейной?
Закину ещё раз.
Как доказать непрерывность для гомеоморфности? Я понимаю, что надо сделать какую-то оценку нормы, но как не знаю.
2+2*2
Я правильно раскрываю скобки? Проверьте просто ход мыслей, а то мало ли.
2(3-5x) - (1+2x) (-5)
6 - 10x - (1-2x) (-5) - т.к. перед скобкой минус, знак в скобке меняется(?)
6 - 10x + 5 + 10x = 11
Все верно?
2(3-5x) - (1+2x) (-5)
6 - 10x - (1-2x) (-5) - т.к. перед скобкой минус, знак в скобке меняется(?)
6 - 10x + 5 + 10x = 11
Все верно?
-(1-2x)(-5)=(-1)(-5)(1-2x)=(-1)(-1)5(1-2x)=5-10x
знак меняется у всех чисел в скобке и перед скобкой
на чем основывается математика?
> т.к. перед скобкой минус, знак в скобке меняется(?)
Да. Но, -(1-2x)(-5) представим, как -ab, где a=1-2x, b=(-5). Умножение - это первое действие. Посему -(ab)=(-(1-2x)b)=(-b+2xb)
На понятии натуральных чисел.
На смысле математематических объектов и их взаимоотношениях.
а понятие о натуральных числах на чем? получается на чувствах и опыте?
Некоторые математические объекты получаются путем идеализации свойств реальных, а так же путем отвлечения от некоторых сторон реальных(или не совсем) объектов с целью выделения их взаимоотношений между собой.
ну мне вот просто интересно рассмотреть определения базовых понятий математики(и не только). ведь определния базовых понятий не формализованы. они обьясняются просто на пальцах, понятия эти могут иметь много разных определений. получается что эти понятия напрямую связаны с нашим восприятием внешнего мира и особенностями мышления? ведь если бы у нас было другое восприятие, то наверное и математика была бы другой
> определения базовых понятий математики
Я тебе больше скажу, они просто неопределяемы. Чувствуются/понимаются/щупаются на очевидном интуитивном уровне.
> получается что эти понятия напрямую связаны с нашим восприятием внешнего мира и особенностями мышления?
Да, именно так, ты абсолютно прав.
Покупаете ли вы бумажные книги?
Редко. По ним, конечно, удобнее и увлекательнее. Но нет. И, вообще, хорошая литература не всегда есть в продаже.
На dxdy покупают
Ананас, вкочусь еще раз, вопрос по тн программе матшкальник.
Первое что бросается в глаза в этой программе - КОЛЦО ЦЕЛЫХ ЧИСЕЛ. КОЛЬЦА, ПОЛЯ ВЫЧЕТОВ вот это все.
Чтож должен прочесть мимокрокодил, чтоб понять и освоить? Может в шапке все есть, а мне и невдомек
Первое что бросается в глаза в этой программе - КОЛЦО ЦЕЛЫХ ЧИСЕЛ. КОЛЬЦА, ПОЛЯ ВЫЧЕТОВ вот это все.
Чтож должен прочесть мимокрокодил, чтоб понять и освоить? Может в шапке все есть, а мне и невдомек
Да. Я эстет и люблю книги.
Пикрелейтед. Для алгебры (к ней относятся кольца и поля) достаточно ван дер Вардена.
Любой учедник открой и тебе там пояснят с 2эпсилон и 2дельта как доказывается.
Объясните-ка кое что пожалуйста - вот начал я читать, допустим, Курс Высшей Математики от Смирнова (с самого начала, естественно), и наткнулся на логарифмирование. Он к нему относится как к известной операции, посему вопрос: Куда относится логарифмирование в математике? В какой теме его искать, либо какой книге прочитать про логарифмы? Возможно ли что я ещё какие-то основы пропустил?
Прочитай справочник по математике для школьника.
Дублирую из другого треда:
Сколько из алгебры/мат.логики/дискры/матана можно заботать за лето ? При условии что что с полного нуля .
Сколько из алгебры/мат.логики/дискры/матана можно заботать за лето ? При условии что что с полного нуля .
Полный нуль - понятие относительное.
Лемма Йонеды
Первая теорема об изоморфизме.
Векторное пространство
Определение степенной, показательной, логарифмической и тригонометрической функций
Системы из двух линейных уравнений
Решение квадратных уравнений
Решение линейных уравнений
Таблица умножения
Таблица сложения
Рисование цифр
Умение писать
Умение читать
* Умение разговаривать
Ты на каком уровне?
> Куда относится логарифмирование в математике
Переформулируй, непонятно что ты хочешь
А вы на каком уровне математики?
Дан N. Как можно найти количество всех решений для уравнения:
1a+5b+10c+25e+50e=n
??
1a+5b+10c+25e+50e=n
??
> Определение степенной, показательной, логарифмической и тригонометрической функций
This с включением всего предыдущего.
Элементарная теория множеств, первый семестр матана (вплоть до теоремы Тейлора), простая алгебра - определение основных структур, операции с матрицами, решение уравнений, элементарная общая топология (вплоть до критериев компактности).
Поинтересуюсь, хоть это субъективно, но такой результат будет при каких усилиях?
Ежедневно по нескольку страниц каждый день лета. Сначала будет охуевание от абстрактности, но самое большее через месяц мозг адаптируется и обучение резко ускорится.
Благодарю.
Если что, запланированное государством количество часов можно посмотреть во ФГОСах.
http://www.edu.ru/db/cgi-bin/portal/spe/spe_new_list.plx?substr=&st=all&qual=0
Но когда учишься сам - это не то же самое, чем когда сидишь в душной поточной аудитории.
Есть задачка сделать выборку по кусочному рекурсивному распределению. В мате я шарю на уровне школьного курса, то есть вообще не шарю. Прошу, направь меня в нужную сторону, анончик. Ну и литературы годной посоветуй по теме, плз.
Масса не изменяется, почитай про это у Окуня https://mipt.ru/education/chair/physics/S_I/method/Okun.pdf
>Возможно ли что я ещё какие-то основы пропустил?
Скорее всего
Ничего не понимаю в этом построении правильных многоугольников, какая-то квадратура круга... Можно это пропустить без вреда для дальнейшего понимания?
В матане*
Слоуфикс
А что думает по этому поводу Карасик?
Категорически воспрещено пропускать непонятное
А вот мне, да, полагаю, и другим просвященным товарищам, было бы интересно узнать мнение уважаемого научного сообщесвта.
Особенно интересно было бы услышать выдающегося ученого де Хованье
http://www.inp.nsk.su/~telnov/mech/lectures/telnov-mechanika-and-TO.pdf
Вот тут весьма понятно, да и сам учебник интересный
Это нормально, что если не понял интуитивно, то значит, что не понял от слова совсем, сколько ни бейся в закономерности построения всяких выражений из буковок и символов?
И что с первого раза некоторые понятия не даются, и всё же полезно иногда побиться лбом, пытаясь уразуметь хоть что-нибудь? Сейчас вот непонятным образом допер до смысла теоремы, которую раза два пытался осилить с частичным результатом.
И что с первого раза некоторые понятия не даются, и всё же полезно иногда побиться лбом, пытаясь уразуметь хоть что-нибудь? Сейчас вот непонятным образом допер до смысла теоремы, которую раза два пытался осилить с частичным результатом.
Понял - расскажи другому. Иначе как понять, что и вправду понял? Вдруг не только не понял, а еще и наебал сам себя, вздумав, что понял?
Короче, как Фенмэн делал - сможешь так же пояснить теорему?
Ну, этот рассказ будет абсолютно неформальным, с точки зрения того, как заковыристо излагал автор учебника или лекции.
Да, было бы неплохо обсудить, но не с кем, знакомых, знакомых с математикой, у меня нет.
>Понял - расскажи другому.
Двачую. Очень эффективно. Причём чем больше объясняешь тем лучше понимаешь сам.
Вот и у меня беда такого же рода, хочется пообсуждать простейшую математику, и не с кем. Кот убегает, знакомые не заинтересованы. По тырнетам - не то. А так хотелось ы собираться по вечерам пятницы с посонами и решать задачки из олимпиад для 6го класса! Увы.
А здесь почему не обсуждать? Или нерелейтед? Может быть тогда есть соответствующий тред на доске? Потому что мне бы тоже хотелось пообсуждать где-то.
Мне стыдно. Это т-такое интимное дело, а тут шизики всякие туда-сюда ходят...
Лол.
Блядь, такое позорище, кстати. Скачал сегодня с рутрекера сборник книжек по арифметике, там была книга с олимпиадными задачками. Среди них была одна. Я 12 листов исписал ебанутыми формулами и дробями, пока не сдался и не подсмотрел решение, оказавшееся унизительно простым.
> пока не сдался и не подсмотрел решение
Вот так вообще нельзя делать, сам много воли потратил, чтобы так не делать.
Соглашусь. Пока шел самостоятельно, хоть и не туда, все таки думал башкой. А так глянул решение, и весь интерес пропал.
Небось была на уровне ящика, да!?
Вы просто ненавидите все ящиковое.
>ящика
А что за ящик, уже который раз его вижу.
Вторая культура это
А сама задача?
Еще при маттредах в сци я написал что долго реал одну простую задачку.
Меня спросили какую.
Я написал что нужно рассчитать сколько дерева нужно взять чтобы сделать ящик для песка с квадратным дном на 40 литров с минимальными затратами дерева.
Эту задачку где то три треда решали в вольфраме и маткаде и пришли к выводу что это н-мерная сфера с н стремящимся к бесконечности.
охуетьПонятно, лол.
Ты о какой задачке?
Хороший был тред, как щас помню
Да про ящик.
Создайте тред про олимпиадные задачки, чо вы как это самое. Чувак вон про книжку Мендельсона создавал, но только как-то не особо взлетело. А вас тут двое уже, шансы повышаются. Только модерируемым его сделать не забудьте, а то засрут-с.
х^2 площадь основания квадрата ящика
у высота
x^2y=40 объем
y=40/x^2
160x/x^2+x^2 площадь дерева на ящик
(160/x)+x сокращаем на х
-160/x^2+1 производная
-160/x^2+1=0
x=~12.64
y=~0.25
Хуйня, в первые же пару постов решили.
Как тот анон в сци, с началами эвклида.
Дададда, было бы круто.
Знач, ОП должен будет задавать темп чтения книги - решения задач, остальные будут бурлеть вокруг.
Нет-нет, олимпиадки точно не мое. Я с основами ковыряюсь.
>И что с первого раза некоторые понятия не даются, и всё же полезно иногда побиться лбом, пытаясь уразуметь хоть что-нибудь?
Это нормально, если, конечно, ты не на каждом определении спотыкаешься. На усвоение некоторых понятий может уйти очень много времени, но нужно их долбить (либо ждать, когда они сами в голове уложатся). Очень хорошо в этом плане помогают различные примеры, иллюстрации, практика. Где их взять? Если всё совсем плохо, можно и самому придумать (недаром же тебе мозг дан). Конечно, если ты неделю сидишь над одной теоремой, то есть смысл посмотреть в другом учебнике, спросить знакомого, etc. Если у тебя так с каждой теоремой/определением, стоит, наверно, взять учебник полегче.
>Сейчас вот непонятным образом допер до смысла теоремы, которую раза два пытался осилить с частичным результатом.
Что у тебя вызывало затруднения?
Как доказываются формулы площадей в планиметрии? Найти не могу доказательства, лишь формулы даны.
Площади плоских фигур?
Да.
Записать уравнение Эйлера для задачи со свободными концами и недостающие граничные условия
Что делать дальше? помогите пожалуйста, уже ничего не понимаю
Где можно почитать про корни уравнений и их свойства?
Задача о размене монет или как-то так.
Cмотрите, какая беда, поцыки. У Зоорича окрестность точки a для функции на E f : E → ℝ обозначается как UE(a), что буквально означает E ∩ U(a). И я вот что-то не вдупляю в упор, какой в этом смысл, если U(a) ⊂ E ⇒ E ∩ U(a) = U(a)?
То есть, это видится как очевидная тавтология, мол собственное подмножество области определения, содержащее точку a есть собственное подмножество ножества E. Или всё-таки нет?
>U(a) ⊂ E
Это неверно. Простой пример: функция задана только в рациональных точках, то есть f : ℚ → ℝ. Окрестность U(a) точки a — множество, включающее в себя все действительные числа, поэтому для f смысла иметь не будет, а ℚ ∩ U(a) смысл иметь будет, ибо в таком случае в каждой точке окрестности функции определена.
>U(a) ⊂ E
Это не так.
U - это интервал вида (a;b), где a и b дейси. числа.
Возьми E={0}.
*дейст.
Бамп задаче. Ну же топологи, где вы?
Ага. Понял. Спасибо.
А Борсук-Улам не на эту тему, случаем?
Как такое делать?
графически
О, тоже идея, благодарствую. А аналитически никак?
Никак. Можно вводить функции которые дают решение уравнению 3^{x}=x. Однако авторы задачника данные вещи не подразумевают.
>А Борсук-Улам не на эту тему, случаем?
Если ты про это, то нет.
>https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%91%D0%BE%D1%80%D1%81%D1%83%D0%BA%D0%B0_%E2%80%94_%D0%A3%D0%BB%D0%B0%D0%BC%D0%B0
Нет. Там, там непрерывность уже подразумивается. А здесь мне её и нужно доказать.
Ачто вот это
>{x}
значит, если не секрет?
Просто скобка.
А как вольфрам получает это?
>Можно вводить функции которые дают решение уравнению
Через такие функции и решает.
a^{b} нотация для: a возвести в степень b
В английской вики, кстати, есть явный вид решения твоего уравнения.
https://en.wikipedia.org/wiki/Lambert_W_function
>Example 1
Насколько я знаю так обозначается дробная часть числа, но тут может быть другой смысл.
https://ru.wikipedia.org/wiki/%D0%94%D1%80%D0%BE%D0%B1%D0%BD%D0%B0%D1%8F_%D1%87%D0%B0%D1%81%D1%82%D1%8C
Cкорее это просто латех-синтаксис для Xn = X^{n}, который часто используют по привычке.
А как гуглить "степени" в в теории вычислимости что это за зверь? Обозначались как идеалы "(а)"
Начал читать "Начала" Евклида. Столнулся с тем, что на вики цитаты из книги с другим переводом, чем последний вроде изданный русский перевод Петрушевского. И перевод на вики мне нравится в разы больше. Например:
Вики: Прямая линия есть та, которая равно лежит на всех своих точках.
Петрушевский: Прямая линия есть та, которая равно расположена по отношению к точкам на ней.
Вики: Плоская поверхность есть та, которая равно лежит на всех своих линиях.
Петрушевский: Плоская поверхность есть та, которая равно расположена по отношению к прямым на ней.
Вопрос: Откуда взят перевод на вики? Или это чисто перевод сделанный на википедии? Есть ли таки альтернативы Петрушевскому? Мб есть изначально англоязычные издания, переведенные на русский?
Вики: Прямая линия есть та, которая равно лежит на всех своих точках.
Петрушевский: Прямая линия есть та, которая равно расположена по отношению к точкам на ней.
Вики: Плоская поверхность есть та, которая равно лежит на всех своих линиях.
Петрушевский: Плоская поверхность есть та, которая равно расположена по отношению к прямым на ней.
Вопрос: Откуда взят перевод на вики? Или это чисто перевод сделанный на википедии? Есть ли таки альтернативы Петрушевскому? Мб есть изначально англоязычные издания, переведенные на русский?
Забавное наблюдение:
Если читая предисловие к Математической шкатулке заменять слова математика или занятия математикой на что-то вроде "революционная деятельность", или "вооруженная борьба", то получится полупризыв полу гайд к этим самым занятиям.
Совейские книги такие совейские
Если читая предисловие к Математической шкатулке заменять слова математика или занятия математикой на что-то вроде "революционная деятельность", или "вооруженная борьба", то получится полупризыв полу гайд к этим самым занятиям.
Совейские книги такие совейские
У кого-нибудь было такое, что сперва математика не очень, нравилась, а потом начала заходить?
> У кого-нибудь было такое, что сперва математика не очень нравилась, а потом начала заходить?
Фикс
> Последнее по времени полное академическое издание было опубликовано в 1949—1951 годах, перевод с греческого и комментарии — Дмитрия Мордухай-Болтовского.
Этот перевод ты скорее всего и читаешь, а перевод Петрушевского был сделан в 1819—1835 гг. Вот твои определения из Петрушевского:
> Прямая линія есть та, которая лежитъ равно своими точками.
> Плоская поверхность или плоскость есть та, которая лежитъ равно своими прямыми линіями.
Было и есть так, что я поначалу терпеть не мог матешу, и сосал в ней по всем фронтам. А теперь вдруг доставляет.
Вот я про нее и говорю, в сицп задание реализовать итеративный вариант процедуры размена
>Как можно найти количество всех решений для уравнения:
Если не ошибаюсь, то это комбинаторика, производящие функции и всё такое. Составляешь производящую функцию, ищешь коэффициент при zn/
Сейчас тетрадь по комбинаторике отрою.
Или не нужно, сам разберёшься?
Бамп
Каких именно уравнений?
Различных дзета-функций
Степенных.
Есть теория о том что у уравнения н степени есть н корней, разных или одинаковых, про произведение разности корней которое равно самому степенному уравнению
Ананас, сейчас упорно тружусь в постижении арифметики, автор Никольский.
У меня сложилось впечатление, после нескольких часов, что меня наебывают. Хуже чем в b.
Задачка - восстановить вычисления, считая что одинаковые буквы это одинаковые цифры, а разные буквы - разные цифры.
Либо я упоролся, либо задачка не имеет решения
ДЕТАЛЬ
+ ДЕТАЛЬ = ИЗДЕЛИЕ
Пример записан в столбик.
Почему я вдруг решил, что меня троллят? Потому что Ь + Ь = Е, и тут же Т + Т = Е. Так быть не может, посему предполагаем, что в Т + Т = Е есть единичка перенесенная из младшего разряда. А ВЕДЬ БЛЯТЬ ЕСЛИ ЕДИничка делает удвоенное Т четным, то блять Т + Т само чтоли нечетное чтоли? Моск кипит уже.
У меня сложилось впечатление, после нескольких часов, что меня наебывают. Хуже чем в b.
Задачка - восстановить вычисления, считая что одинаковые буквы это одинаковые цифры, а разные буквы - разные цифры.
Либо я упоролся, либо задачка не имеет решения
ДЕТАЛЬ
+ ДЕТАЛЬ = ИЗДЕЛИЕ
Пример записан в столбик.
Почему я вдруг решил, что меня троллят? Потому что Ь + Ь = Е, и тут же Т + Т = Е. Так быть не может, посему предполагаем, что в Т + Т = Е есть единичка перенесенная из младшего разряда. А ВЕДЬ БЛЯТЬ ЕСЛИ ЕДИничка делает удвоенное Т четным, то блять Т + Т само чтоли нечетное чтоли? Моск кипит уже.
Это которая в самом начале там?
>реализовать итеративный вариант процедуры размена
Блядь, а я рекурсивный стал делать. Ща сек, уже всё вспомнил.
два нуля и два пятака мб
Пробовал, не подходит.
Аж голова тяжелая, пойду прогуляюсь
Я запутался, например 7 мы сколькими способами можем разложить? Или 10?
7 по идее четырьмя, 10 девятью?
Да, залупа, я считал, что 1 1 5, 5 1 1, 1 5 1 три разных способа.
В процессе решения другой задачи, вышел к такой. Рассмотрим кортежи длины n:
(a1, a2, ..., an), при этом
- Каждый элемент натуральное из [1, m]
- Каждый элемент строго больше предыдущего (ai > aj), при i > j
Сколько существует таких кортежей?
Сам пришел к рекуррентной формуле, в виде суммы от числа кортежей длины на 1 меньше, но не знаю как получить точное число.
Для оригинальной задачи по комбе надо найти сумму всех таких комбинаций, при длине от 1 до m
На случай, если где-то плохо описал, примеры:
При n = 3, m = 4, все кортежи:
> (1, 2, 3)
> (1, 2, 4)
> (2, 3, 4)
(a1, a2, ..., an), при этом
- Каждый элемент натуральное из [1, m]
- Каждый элемент строго больше предыдущего (ai > aj), при i > j
Сколько существует таких кортежей?
Сам пришел к рекуррентной формуле, в виде суммы от числа кортежей длины на 1 меньше, но не знаю как получить точное число.
Для оригинальной задачи по комбе надо найти сумму всех таких комбинаций, при длине от 1 до m
На случай, если где-то плохо описал, примеры:
При n = 3, m = 4, все кортежи:
> (1, 2, 3)
> (1, 2, 4)
> (2, 3, 4)
>Для оригинальной задачи по комбе надо найти сумму всех таких комбинаций, при длине от 1 до m
до n фикс
Ты про какую задачу?
>Дан N. Как можно найти количество всех решений для уравнения:
1a+5b+10c+25e+50e=n
Эту? Если да, то тебе нужно написать функцию разложения в ряд Тейлора в 0 по сути, коэффициент при z^n будет искомым числом.
http://www.wolframalpha.com/input/?i=series+1%2F((1-z)(1-z%5E5)(1-z%5E10)(1-z%5E25)(1-z%5E50))
Сожрало.
Я понял, про какой ты пост, но я вообще другой анон. Моя задача из комбинаторики Виленкина, и решается без числа кортежей
Нифига не понял, ты тот или не тот?
А у тебя что за задача?
Я вот сейчас сижу уже хз сколько, пытаюсь явную формулу вывести для коэффициентов, роюсь в тетрадях, лол.
Может поможет кто-то?
То есть нужно по сумме ряда найти формулу для частичной суммы. Наверняка ведь тут кто-то знает, как это сделать.
Там может быть и двойка перенесена. Суммирование дало 19, 10 перенесли, а потом с прошлого разряда пришла единичка, стало вместо 9 10 и перешло в следующий разряд.
На окружность есть n точек. Сколько выпуклых многоугольников можно построить?
Решение мега простое, проблем нет. Но пока думал, задумался над . С этим есть проблемы
Если я в математике полный нуль (дико проёбывал школу), но сейчас решил взяться за неё, потому что по работе есть такая необходимость, за какую книжку или учебник браться? Неужели учебники со второго и по одиннадцатый класс?
Алсо, в шапке большинство книг для нубов в каких-то всратых допотопных форматах, а вот в fb2, mobi или pdf ничего почему-то нет.
Стандартный формат математических книг - djvu. Советую поставить ридер.
Да, тебе нужно прочитать школьные учебники. Лучше читать не сами учебники (они нечитаемые), а какие-нибудь типа справочники по школьной математике.
Если знаешь арифметику, то можешь начинать с 7го. Если нет, то класса с 5го.
Суммирование в примере не может дать 19, к сожалению. Там же одинаковые числа складываются, друг с другом, тобишь умножаются на джва
Короче, анон это пиздец, лол. С комбинаторикой лучше не связываться, с виду простенько, а на деле весь день потратил.
def h(n):
if n==0:
return 1
if n<0:
return 0
return h(n-1)+h(n-5)+h(n-10)+h(n-25)+h(n-50)\
-h(n-1-5)-h(n-1-10)-h(n-1-25)-h(n-1-50)-h(n-5-10)-h(n-5-25)-h(n-5-50)-h(n-10-25)-h(n-10-50)-h(n-25-50)\
+h(n-1-5-10)+h(n-1-5-25)+h(n-1-5-50)+h(n-1-10-25)+h(n-1-10-50)+h(n-1-25-50)+h(n-5-10-25)+h(n-5-10-50)+h(n-5-25-50)+h(n-10-25-50)\
-h(n-1-5-10-25)-h(n-1-5-10-50)-h(n-1-5-25-50)-h(n-1-10-25-50)-h(n-5-10-25-50)\
+h(n-1-5-10-25-50)
print(h(40))
Вот рекурсивное решение, раскручивай в цикл, упрощай, делай массив с первыми значениями, динамическое погромирование вся хуйня. Ебал я комбинаторику вот что.
Знак \ это не деление а перенос строки, так то это всё одна строчка.
>массив с первыми значениями
По идее с первыми 50ю, но могу ошибаться, мб это не нужно.
>реализовать итеративный вариант процедуры размена
>найти количество всех решений для уравнения:
>1a+5b+10c+25e+50e=n
Ладно, короче, лови.
def h(n):
if n<0:
return 0
n+=1
bottom = 0
border = 10
bottom += 1
solutions = [1,1,1,1,1,
2,2,2,2,2,
4,4,4,4,4,
6,6,6,6,6,
9,9,9,9,9,
13,13,13,13,13,
18,18,18,18,18,
24,24,24,24,24,
31,31,31,31,31,
39,39,39,39,39,
50,50,50,50,50,
62,62,62,62,62,
77,77,77,77,77,
93,93,93,93,93,
112,112,112,112,112,
134,134,134,134,134,
159,159,159,159,159,
187,187,187,187,187,
218,218,218,218,218]
if n<=len(solutions):
return solutions[n]
i=len(solutions)
while i<n:
solutions.append(solutions[i-1]+solutions[i-5]+solutions[i-10]+solutions[i-25]+solutions[i-50]-solutions[i-6]-solutions[i-11]-solutions[i-26]-solutions[i-51]-solutions[i-15]-solutions[i-30]-solutions[i-55]-solutions[i-35]-solutions[i-60]-solutions[i-75]+solutions[i-16]+solutions[i-31]+solutions[i-56]+solutions[i-36]+solutions[i-61]+solutions[i-76]+solutions[i-40]+solutions[i-65]+solutions[i-80]+solutions[i-85]-solutions[i-41]-solutions[i-66]-solutions[i-81]-solutions[i-86]-solutions[i-90]+solutions[i-91])
i+=1
return solutions[-1]
print(h(166))
Если нигде не наебался, что возможно, в формуле, например, то количество всех решений, количество способов разменять n это коэффициенты при z^n. Вроде всё верно.
>bottom = 0
>border = 10
>bottom += 1
Это удали, это для отладки.
Возможно, тут можно вообще без массива обойтись, как например с вычислением нтого Фибоначчи тупо две переменных, тут будет 32 правда, но в теории вроде можно, уже сам посмотри.
Откуда ты вообще эту задачу нарыл?
Если ты знаел, что это за задача, почему ты просто не нагуглил решение?
https://stackoverflow.com/questions/1485022/sicp-making-change
Ь = 9, Т = 4.
Если я правильно понял,то то, что он предлагает, это делить каждое следующее n, и если да, то прибавлять к результатунаивное решение, то, что изначально подумал, проблема в том, что это неверно, например на 10 мы прибавляем 2, на 15 тоже 2, на 20 3, на 25 4, на 30 уже 6, 40 7, 45 8, а на 50 уже 11. Если я правильно понял то, что он предлагает, это не сработает.
>In short, (fact 5) "evolves a linear recursive process", since it uses stack space linear in its argument, and (fact-iter 5) "evolves an iterative process", since it uses constant stack space, no matter how big its argument is.
>By "iterative process", they mean one that doesn't use more than a fixed, small amount of stack space (in SchemeLanguage, which does TailCallOptimization).
http://wiki.c2.com/?SicpIterationExercise
Вот тут вроде бы пишут, что под итерацией там имелась ввиду не совсем итерация.
Хотя мб я не понял. Фиг с ним, короче.
Спасибо, господа.
бамп задаче
Какой смысл у перпендикуляра к кривой в точке и подкасательной?
Переделал с циклическим стеком. Хз, это всё ок, конечно, но там ни слова не сказано о том, как находить коэффы сами. Без них можно только за щеку взять на мой взгляд.
class List(list):
def __getitem__(self, key):
key %= len(self)
return super(List, self).__getitem__(key)
def __setitem__(self, key, value):
# optional processing here
key%=len(self)
super(List, self).__setitem__(key, value)
def f(n):
solutions=List(0 for x in range(91))
solutions[0]=1
i=0
while i<n:
solutions=(solutions[i-1]+solutions[i-5]+solutions[i-10]+solutions[i-25]+solutions[i-50]-solutions[i-6]-solutions[i-11]-solutions[i-26]-solutions[i-51]-solutions[i-15]-solutions[i-30]-solutions[i-55]-solutions[i-35]-solutions[i-60]-solutions[i-75]+solutions[i-16]+solutions[i-31]+solutions[i-56]+solutions[i-36]+solutions[i-61]+solutions[i-76]+solutions[i-40]+solutions[i-65]+solutions[i-80]+solutions[i-85]-solutions[i-41]-solutions[i-66]-solutions[i-81]-solutions[i-86]-solutions[i-90]+solutions[i-91])
i+=1
return solutions[n-1]
print(f(16600))
>коэффы
Вернее само соотношение в общем, ты понял.
h(n)=h(n-1)+h(n-5)+...+h(n-91), я не представляю как читатель без матподготовки, комбинаторики, производящих функци и прочего говна должен был до этого допереть. Хотя мб это интуитивно, а я тупой.
>с циклическим стеком
Ну не циклическим даже, по сути тут 32 переменных.
В которых хранятся нужные на данном этапе значения. Это не стек ни разу, 32 переменных,просто для удобства сделал.
> 32 переменных
Только их 91, 32 мало, съедаются, ну не мудрено, всегда же если рекуррентная ебала, нужно вычислить первые значения. Только обычно степень 10, а не 91, блядь. Ебанутая задача.
Короче вот решение
, если тебе нужно ещё. Но наверняка ты забил хуй ещё днём. Ну и фиг с ним.
>while i<n:
Только тут больше либо равно
>solutions[n-1]
А тут без минус 1.
Да, но во второй версии ее нет , только в draft версии.
Это что за пиздец мужик? Короче вол полная задача:
Итеративная процедура размена n центов, используя 50,25,10,5,1 цент. Для 100 центов ответ 256.
Какой смысл в задаче когда просто смотришь ее решение? Азарта даже нет.
>Для 100 центов ответ 256.
Нет, не может быть. Ответ 292. Ты уверен? потому что я уверен, для сравнения дам тебе ссылку на задачу, похожую на твою, там ответ 343, логика такая же, я проверял у меня там тоже 343 выходит(в вольфрам альфа), если замену в формуле сделать. Я сейчас делаю в общем случае: ввёл 1,5,10,25,50 и n, получил ответ, для произвольного числа короче. Вот ссылка
http://dxdy.ru/topic10235.html
В list scheme нет массивов.
У тебя странное рекурсивное решение, оригинальный процесс образует древесную рекурсию. Пикрелейтед
Сочетания из m по n. Сумма C(m, n) для n от 0 до m равна 2^m. И ты забыл ещё один кортеж: (1, 3, 4).
>Итеративная процедура размена n центов, используя 50,25,10,5,1 цент.
Вот тут ответ самый оптимальный по времени и памяти. Если подождёшь, я сейчас допиливаю для произвольного числа.
Да, извини, ответ 292
Это рекурсивное решение. Я его развернул в последней версии. Если подождёшь полчаса, доделаю для произвольного уравнения и N.
А может два часа. как пойдёт, уже спать хотел, лол,встал и решил доделать.
А зачем ты тогда на дваче решение спрашиваешь, если тебе азарт нужен?
Да ладно, анон, он её хуй бы когда решил без математики.
>Азарта даже нет.
Если хочешь, могу тебе расписать решение.
Короче вот, даёшь на вход массив коэффициентов и N, получаешь количество искомое. Проверил для того случая, получил 343, вроде не должно таких совпадений быть, лол. Так скинуть могу, но засирается тред, к тому же вакаба скобки в посте выше съела.
Функция Поверсет это булеан по сути, все подмножества множества, дальше от этого пляшем, создаётся массив с особыми свойствами, ну типа как циклический, туда закидываются значения и тд, значения индексов от булеана вычисляются, по сути туда весь тот ужас с цифрами спрятал. разберёшься.
Объяснить почему так?
Бля, coefficient через k, подобосрался.
По моему что то неправильно посчитано.
В общем у нас есть n неразличимых предметов и k различимым ящиков неограниченной вместимости, но в хотя бы одном ящике должен быть хотя бы один предмет вот это важно, без этого мы не можем применять аппарат производящих функций, при условии, что порядок не важен. Тогда мы можем составить производящие функции:
f1(z)=1+z+z2+z3+..+zn=1/(1-z)
f5(z)=1+z+z2+z3+..+zn=1/(1-z)
f10(z)=1+z10+z20+..+z10n=1/(1-z10)
f25(z)=1+z25+z50+..+z50n=1/(1-z50)
f50(z)=1+z50+z100+..+z50n=1/(1-z100)
Про производящие функции можешь почитать тут, например
http://www.genfunc.ru/
если коротко, то это сорт оф индикаторная функция, z здесь это элемент (0,1,0,0...), z2 это (0,0,1,0,0...), гугли формальные степенные ряды в общем. Грубо говоря, если у нас есть z в какой-то степени n, то это значит, что в ящик, описываемый этой функцией, мы можем положить n предметов(или не положить ни одного, z0=1). Для всей этой братии введены операции сложения, умножения и свёртки, но это хуй с ним.
Дык вот, к чему я всё это:
Наша искомая функция будет произведением функций выше:
h(z)=f1(z)f5(z)f10(z)f25(z)f50(z)=пикрелейтед
Дальше мы можем разложить пикрейтед в ряд Тейлора в точке z0=0 и получить многочлен, коэффициенты которого при zn и будут тем самым количеством способов разложить
>n неразличимых предметов и k различимым ящиков неограниченной вместимости, но в хотя бы одном ящике должен быть хотя бы один предмет
Проблема в том, что охуеешь это вычислять, вычислялка не выросла%%ну у меня так, вольфрам молодец, конечно, но о 1000 члене производной хотя бы речи не идёт. Но можно охуеть и заметить, что данную формулу можно вывести рекуррентно по формуле включений-исключений, например для 2, 4 это было бы:
h(n)=h(n-2)+h(n-4)-h(n-2-4)=h(n-2)+h(n-4)-h(n-6)
Для 1,2,3 это было бы:
h(n)=h(n-1)+h(n-2)+h(n-3)-h(n-1-2)-h(n-1-3)-h(n-2-3)+h(n-1-2-3)=h(n-1)+h(n-2)-h(n-4)-h(n-5)+h(n-6)
Ну а для твоей задачи я ебал это выписывать, 25-1=31 член.
Дальше понятно, делаем рекурсивную версию программы, затем оптимизируем, разворачиваем рекурсию с помощью массива с динамически увеличивающимся размером, дальше оптимизируем, делаем размер фиксированным, дальше решаем в общем случае. Как-то так. Я не ебу, что хотел сказать автор, помещая эту задачу в учебник для вкатывающегося погромиста, может быть он знатный троляка, да.
Забыл: эта задача имеет несколько переформулировок, одна из которых про монетки, а другая про количество решений уравнений в положительных числах.
Натуральных. Ну ты понел.
>вот это важно, без этого мы не можем применять аппарат производящих функций
Я тебя наебал, это верно только когда мы юзаем композицию функций.
Нет, не наебал.
Там же есть более хитрый способ. В книге Полиа Сеге одно из первых заданий про размен монет. Там была задача подсчитать при n=60. И в ответе была ссылка на то, как хитро считать. Я уже постил в тред подобную задачу и просил мне перевести ту статью на немецком, но на это резко все забили.
Частично наебал, это разрешено только если a0=0. Вся проблема в том, что там получается деление на z, а z не имеет обратного по отношению к операции умножения.
Ну способ с включениями-исключениями относительно хитрый. Иначе пришлось бы в ряд раскладывать, искать 1000 производную и 1000 факториал и всё такое прочее.
господь, какой я долбоеб
В итоге на первую и вторую задачу ответ один и тот же, лол. Почему ты не посмотрел ответ на вторую задачу? Там же всё описано.
ой, соряныч. Там другое условие. Ну ка ща прожку проверю.
Фишка то в том, что эта задача в книге дедов 64 года. У них не было компа и я хотел узнать, как они решали без него.
В первой надо получить имено числовой результат.
Где-то с минусом наебался, но в целом ок.
>У них не было компа и я хотел узнать, как они решали без него.
Ну комп не нужен, есть же формула рекуррентная, брать да составлять, я хз. А может ты и прав и есть какой-то хитрый способ.
А, не с минусом, чётное количество элементов просто, тогда на минус 1 домножить нужно.
Я даже ту статью, на которую указывает ответ находил. Но! Она на немецком.
>n=100
фикс
Скинь мб, позырю, я не немец, конечно, но мало ли, хотя бы посмотрю верный ход мыслей или там и правда нечто другое.
Ниже скрин ответа. И у тебя в учебнике такой же.
Ладно, пойду искать.
Ща сижу, короче, простые числа туда подставляю, хз чего добиваюсь, лол.
Ок, спасибо.
Не, это не оно. Да хз, он там вроде тоже рекуррентно выводит.
Лол, анон, статье сто лет.
>1918
АвторDr. W. Ahrens (auth.)
Бамп
Ты прав.
Анонасий, ты читал Высшую арифметику Девенпорта? Стоит ли прочесть, если я вот только вот школьную арифметику повторил, а за алгербу даж не брался еще?
> у уравнения н степени есть н корней
Это так, но пруфануть, привести теорему не смогу, вообще забыл, откуда это.
>Число комплексных корней многочлена с комплексными коэффициентами степени n, учитывая кратные корни кратное количество раз, равно n.
Полистай, посмотри что внутри. Наверное и алгебру придётся повторить.
НУ так а почитать где про это вот можно?
Я же говорю
>но пруфануть, привести теорему не смогу, вообще забыл, откуда это.
Используй гугл, Люк!
Я решил стать адептом функционального программирования, и ковыряюсь в алгоритмах. Сейчас ебусь с возведением в степень по модулю. Все ок, только не могу понять, почему a^n mod b равно (a * (a^(n-1) mod b)) mod b.
Буду рад, если кто-нибудь объяснит.э
Буду рад, если кто-нибудь объяснит.э
Привет, math.
Вопрос такого рода у меня:
в книгах где описывается задача о четырёх красках даётся визуально понятное объяснение эквивалентности сферы и плоскости(протыкаем любую область, начинаем растягивать, укладываем на плоскость), а вот эквивалентность плоскости сфере не встречал.
Не встречал ли кто-нибудь подобное доказательство(объяснение)?
Из того что я попробовал, всё идёт скорее всего к индуктивности, что не так интуитивно понятно.
Спасибо!
Вопрос такого рода у меня:
в книгах где описывается задача о четырёх красках даётся визуально понятное объяснение эквивалентности сферы и плоскости(протыкаем любую область, начинаем растягивать, укладываем на плоскость), а вот эквивалентность плоскости сфере не встречал.
Не встречал ли кто-нибудь подобное доказательство(объяснение)?
Из того что я попробовал, всё идёт скорее всего к индуктивности, что не так интуитивно понятно.
Спасибо!
В учебнике алгебры (Винберг, Кострикин, etc).
(a (a^{n-1} mod b)) mod b = (a (a^{n-1} - qb)) mod b = (a^n - aqb) mod b = a^n mod b
Спасибо! Теперь не буду читать про быстрые алгоритмы сортировки, буду думать, почему я такой тупой. большое спасибо, бро
Как тут вообще одно к другому и причём тут функциональное программирование?
Дифференциал это то что на картинке, а дифференируемость что тогда? Возможность сделать то что на картинке или что?
Я то думал что дифференциал это превращение бесконечно малого отрезка какой то кривой в касательную прямую
Я то думал что дифференциал это превращение бесконечно малого отрезка какой то кривой в касательную прямую
Есть задачка:
Написать функцию, делающую одну выборку по кусочному рекурсивному распределению.
- вход: распределение
- выход: число
В матане я вообще не шарю, но вот что нагуглил:
на первом пике похоже та самая функция распределения которую я должен принимать на входе. 0, 0.1, 0.7 это вероятность события, а дальше идет интервал. На втором пике определение выборки, которую мне нужно найти, только это не число, а массив. Хз чому так.
Отсюда вопрос,все ли я правильно понимаю и как мне это распределение превратить в ту самую выборку.
Написать функцию, делающую одну выборку по кусочному рекурсивному распределению.
- вход: распределение
- выход: число
В матане я вообще не шарю, но вот что нагуглил:
на первом пике похоже та самая функция распределения которую я должен принимать на входе. 0, 0.1, 0.7 это вероятность события, а дальше идет интервал. На втором пике определение выборки, которую мне нужно найти, только это не число, а массив. Хз чому так.
Отсюда вопрос,все ли я правильно понимаю и как мне это распределение превратить в ту самую выборку.
Тебе в /pr
Причем тут пр? Мне с распределением нужно разобраться, а это математика, так что я по теме тут, всю эту хуйню я сам писать буду, как разберусь, меня просто на правильный путь нужно направить. Не гони меня, анончик, лучше подскажи.
>Причем тут пр?
Действительно, не читай отвечай. Погорячился.
Простым языком, дифференцируемость в точке — возможность построить в этой точке касательную, но строго говоря, дифференцируемость в точке — возможность найти такое линейное отображение, что приращение функции от приращения аргумента будет равно дифференциалу от этого приращения плюс функция бесконечно малая от приращения (если приращение стремится к нулю), а дифференциал — это то самое линейное отображение, то есть функция df(x) : h → f'(x)h.
Короче, если h — приращение аргумента, то f(x+h) - f(x) — приращение функции. Функция дифференцируема, если f(x+h) - f(x) = df(x)(h) + a(x; h), где df(x)(h) — функция линейная по h, a(x; h) — функция бесконечно малая при h→0.
На твоей картинке dy — это значение дифференциала от приращения dx, а не сам дифференциал.
Если правильно понял, у тебя даны вероятности чисел, по ним выдаёшь число. Имитация рандома.
Похоже на то, вот пример, который к задаче приводят:
кусок 1: 0 (вероятность 70%)
кусок 2: нормальное с центром в 1, дисперсия 0.3, мин 0.5, макс 1.5 (вероятность 25%)
кусок 3: равномерное от 2 до 5 (вероятность 5%)
Не совсем понятно, что там на вход подаётся. Есть ссылка на оригинал?
Написать функцию, делающую одну выборку по кусочному рекурсивному распределению
Пример:
кусок 1: 0 (вероятность 70%)
кусок 2: нормальное с центром в 1, дисперсия 0.3, мин 0.5, макс 1.5 (вероятность 25%)
кусок 3: равномерное от 2 до 5 (вероятность 5%)
Вложенность распределений может быть любая, в примере выше - до 2го уровня
Типы поддерживаемых распределений:
- дискретное (+частный случай - точка)
- равномерное
- нормальное
- экспоненциальное
Нужно:
- написать саму функцию
- вход: распределение
- выход: число
- придумать адекватный формат данных для кусочного рекурсивного распределения
- написать тесты показывающие разные варианты использования
Это вся задача.
Ну по идее да, тебе нужно реализовать рандомайзер, в него забиваешь функцию, затем он тебе выплёвывает число, как я понимаю, сколько раз вызовешь, столько раз и выплюнет, отсюда путаница массив/число.
Смотри в сторону математической статистики, там всё это описано.
>рекурсивного распределения
Единственное что я не понимаю, что вот это значит. Может перевод такой?
>рекурсивное распределение
Либо же это что-то вроде вот этого, но тут я тебе не советчик.
https://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%BB%D1%8C%D1%82%D1%80_%D0%9A%D0%B0%D0%BB%D0%BC%D0%B0%D0%BD%D0%B0
>он тебе выплёвывает число
Спасибо, теперь буду понимать что от меня требуется. А посоветовать литературы можешь?
Я и так все облазил, даже парочку советских учебников скачал. Самый годный показался справочник по вероятностным распределениям, вадзинского.
Возможно это значит, что функция в себе может еще парочку таких же содержать.
Спасибо няш, пойду почитаю.
>Спасибо няш, пойду почитаю.
Не нужно, скорее всего это не то, а просто вложенность так автор обозвал, по остальному вот тут ключевых слов уйма, там же и ссылки
https://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B2%D0%B5%D1%80%D0%BE%D1%8F%D1%82%D0%BD%D0%BE%D1%81%D1%82%D0%B5%D0%B9
Блин, ну на это ссылку я с самого начала и наткнулся, там одни формулы и ничего не понятно.
статистика учебник скачать онлайн бесплатно без регистрации торрент носд старфорс
Посоветуйте, пожалуйста, науч-поп по основам статистики, а еще и по вероятностям кроме того (да еще и байесовую в том числе было бы хорошо).
Как вы себя удерживаете в изучении математики? Вам каждый символ кажется каким-то религиозным откровением, наполняющим счастьем или приходиться искать какие-то интересные задачки для ума, хитрости и все в таком духе или что-то другое вообще?
>На твоей картинке dy — это значение дифференциала от приращения dx, а не сам дифференциал.
Опять наебали? Уууууу, пидоры, в плохом смысле этого слова.
>линейное отображение
линейная функция у=кх+с?
>приращение функции от приращения аргумента будет равно дифференциалу от этого приращения плюс функция бесконечно малая от приращения
Это я читал, разница между формулой вычисления производной ф(х+дх)-ф(х)/дх и производной дф(х) равна производной дф(х) плюс э_умножить_дх.
Я понял что тут имеется ввиду тот факт что бесконечно малые при вычислении производной хоть и являются околонулевыми и их можно отбросить, но они все еще остаются способными влиять на результат если сделать шаг вправо-влево.
Это я все к тому что можно ли вкатится в математику через дифференциалы, со всеми пояснениями про бесконечно малые и их сравнение, концепцией бесконечности/неограниченности/необъятности, а потом уже производные с интригалами и тензорами наскоком проходить на основании дифференциала.
Забаньте уже этого мессию.
Небось тот же толстяк что пределы не осилил и поделил математику на правильну и неправильную, арийскую и жыдовскую.
Которые ещё про производную и касательную треды создавал?
db=20*log(v1/v2)
Как выразить из этой формулы v1?
Уже напрочь забыл и алгебру и матан...
Как выразить из этой формулы v1?
Уже напрочь забыл и алгебру и матан...
>линейная функция у=кх+с?
y = kx. Дифференциал df(x) в точке зависит от приращения, то есть df(x)(h) = f'(x)h. Если мы возьмём функцию y = x, то получим, что dx(h) = x'h = h. Далее получим, что df(x)(h) = f'(x)dx(h), а значит, df(x) = f'(x)dx (здесь уже написано равенство функций). Далее f(x+h) - f(x) = df(x)(h) + a(x;h), то есть f(x+h) = f(x) + f'(x)h — уравнение касательной в точке x. Обрати внимание: сам дифференциал — функция вида y = kx, а уравнение касательной в точке — y = kx + c.
>Это я все к тому что можно ли вкатится в математику через дифференциалы, со всеми пояснениями про бесконечно малые и их сравнение, концепцией бесконечности/неограниченности/необъятности, а потом уже производные с интригалами и тензорами наскоком проходить на основании дифференциала.
Начинать надо с предела, ибо дифференциал при построении интеграла Римана тебе ничем не поможет.
Что то я щас с просонья не ПОНИмаю что ты написал про дифференциал, потом разберу.
>Начинать надо с предела
Ну так да. Сперва непрерывность показать, сначала как линию нарисованную не отрывая пера от бумажки, потом через сечения дадаиста. Потом на основании непрерывности вывести бесконечно малые и как их употреблять с картофаном и водовкой, потом сравнение бесконечностей потом суп с котом и наконец дифференциалы.
>с просонья не ПОНИмаю
Рекомендую взять учебник. Там всё это написано более подробно — я же написал очень скомкано.
>сечения дадаиста
Дедекинда? Короче, почитай учебник (или лекции посмотри хотя бы), ибо у тебя каша какая-то. В стандартном курсе анализа путь такой: предел → непрерывность → дифференциал → интеграл.
Сложна, сложна, ничего не понятно. Что делать дабы понять? Зачем так много линий? Если окрасить это в цвета или перевести в музыку станет понятней? Что делать с этой геометрической интерпретацией?
Ты все прекрасно понял. Такое чувство будто первый раз на двощи зашел.
И да, в стандартном учебнике сперва непрерывность и потом предел.
Ибо предел основан на непрерывности. Иначе у функции 1/х были бы производные в точке начала координат.
Потому что ты переусложнение взял.
Графика и уравнения описывают одно и то же но с разных сторон. На какую то вещь удобнее смотреть одной стороны, а другую держать на подсосе, с другой наоборот, с третьей эскобар.
Жутко бомбит от того, что я несколько рассеянный, и когда при чтении доказательства теоремы, допустим, получу интуитивно созерцаемый результат, отложу его в "короткую" память, потом переключаю внимание на чертовы буквы и символы, пока вникну в новый кусок доказательства, старый уже исчезнет из памяти, и новый тоже теряет на этом фоне свой смысл.
Наверное, это и отличает математика от обычного быдла, что у первого память и мозги в целом позволяют быстро и легко переходить от рун на бумаге к интуитивно ясному представлению абстракций в уме, не теряя из виду детали.
Наверное, это и отличает математика от обычного быдла, что у первого память и мозги в целом позволяют быстро и легко переходить от рун на бумаге к интуитивно ясному представлению абстракций в уме, не теряя из виду детали.
Гхм... Эквивалентность же в обе стороны работает, не?
>И да, в стандартном учебнике сперва непрерывность и потом предел.
Честно говоря, я такое видел только в лекциях Львовского и учебнике Шварца, которые стандартными учебниками я бы не назвал.
>Ибо предел основан на непрерывности.
С таким же успехом можно сказать, что непрерывность основана на пределе. Спор из разряда «что было раньше: яйцо или курица?».
>Иначе у функции 1/х были бы производные в точке начала координат.
Ты о чём? Есть три вещи: предел в точке, непрерывность в точе и дифференцируемость в точке. Они находятся в таких соотношениях: дифференцируемость ⇒ непрерывность ⇒ предел. В обратную сторону это не работает, то есть из существования предела не следует непрерывность, а из непрерывности не следует дифференцируемость.
Такая же проблема, даже на элементарнейших примерах, случается, таким же образом сбиваюсь.
изучаю-арифметику-кун
Подвижный интеллект бла-бла-количество объектов одновременно-бла-в памяти. Короче, я удмаю, что эта способность подлежит тренировке до определенной степени хотелось бы верить
А ты попытайся будто рассказать кому-то доказательство этой теоремы и будто кого-то научить.
Ты хоть высшую арифметику учишь, то есть теорию чисел?
Нет конечно, что я, математик что-ли настоящий?
А по поводу этих вот интуитивно-зрительных результатов, - они помоему так и сотруться, если им не придать форму в словах, тоесть не высказать их "из головы".
Это все при условии, что мы об одном и том же явлении
Какую арифметику изучаешь? Я читаю "Основы анализа" Ландау(который Эдмунд, есличо), и теоремы о сложении-умножении сечений поначалу выносили мне мозг, а потом как-то щелкнуло и вроде бы даже дошло, что именно скрывается за подробным строгим доказательством.
Не знаю ни о каком "подвижном интеллекте", рассказы об упорных тренировках вызывают скуку. А процесс внезапного озарения, пусть нередко и ошибочного, происходит где-то в тени сознания, куда я не могу добраться.
Но хочется конечно, чтобы с первого раза все понималось кристально ясно.
Остановимся на принципиальном вопросе о неспособности к математике, который иногда встает при изучении анализа. Проблема имеет, по всей видимости, неожиданное решение. Чем легче человек поддается гипнозу, тем труднее ему дается математика. Причина в следующем.
Тройная спираль Эриксона – три истории, вставленные друг в друга – любого вгоняют в гипнотический транс. И это не сказка, а психологический прием, простой как молоток и эффективный как уголовно наказуемый «двадцать пятый кадр». В математике нечто подобное происходит само собой. В результате многие попадают в состояние транса задолго до того, как то или иное рассуждение услышано до конца. Транс же хорош для восприятия чувств и настроений, но не логических цепочек.
Пояснить сказанное. Спираль Эриксона – это хитрый и вместе с тем очень простой трюк. Рассказывается некая история, которая в середине обрывается, и начинается рассказываться вторая история, которая снова не доводится до конца, и повествование переключается на третью историю. Сознание вынуждено держать в памяти все эти половинчатые истории – и у него оказываются «заняты руки». Охрана снята, дорога к подсознанию свободна, слушатель в трансе.
Да обычную повторяю, решил вот. Потом увидел книгу, о которой писал выше "Высшая арифметика Дэвенпорта", после повторения алгебры за нее возьмусь наверное
На этом же фокусе основаны так сказать цыганские наебочки, их разноцветность одежд, многословие. Так же грузит базаром уголовное быдло, стремясь перегрузить оперативную память лишней инфой и вызвать охранительное торможение, в терминологии этой пасты - транс
От чего охраняет такое торможение?
>не знаю ни о каком подвижном интеллекте
>процесс озарения
>не могу добраться
А мог бы прочитать Каннемана и понять что и куда тут вертится. В теории, конечно
В современном мире разве что от спасающей тебя активности. Например, от попытки уйти с дороги когда на тебя несется Вадик на жигулях.
Согласно этому тексту, к математике я способен слабо, или даже чрезвычайно слабо, на грани полного непонимания. В школе гопота грузила меня базаром, а я терялся и не знал, что им ответить.
Иллюзия понимания мне ни к чему. Приятнее думать, что есть непонятный черный ящик в мозгах, который позволяет тупому дауничу прозревать сложные вещи.
От этого очень хорошо помогает «нисходящее» чтение учебника, то есть при чтении какой-то теоремы нужно сперва её обозреть в целом, понять, по какому принципу построено доказательство, саму структуру, а уже потом углубляться в детали. Ещё хорошо помогает наличие примеров, которые ты можешь постоянно прокручивать в голове при чтении.
>Согласно этому тексту, к математике я способен слабо, или даже чрезвычайно слабо, на грани полного непонимания.
Накручиваешь ты. Память тренируется; воображение, усидчивость, логическое/абстрактное мышление, думаю, тоже. Доказывать это я, конечно же, не буду.
Какие тогда учебники стандартные? Ебаный демидович? Курс куранта? Калькулус тотомаса? Еврейский раССовый жид?
И у этой функции нету ни одного из трех перечисленных пунктов в точке ноля.
И потом, ты же сам пишешь что предел выходит из непрерывности.
Почему же? Просто говорю, как может быть. А может и нет. Мне все-равно, эти охуительные истории от ни черта не смыслящих в работе мозга гопников до одного места. Даже если сам б-г и дьявол спустятся ко мне и докажут, что я математический дебил, я все-равно буду упарываться тем, что нравится, что красиво.
Забыл еще спросить у всяких петухов, чем мне надо заниматься и какое у меня призвание, согласно феншую, ну на большее, чем феншуй, эти рассказы не тянут
>От этого очень хорошо помогает «нисходящее» чтение учебника, то есть при чтении какой-то теоремы нужно сперва её обозреть в целом, понять, по какому принципу построено доказательство, саму структуру, а уже потом углубляться в детали. Ещё хорошо помогает наличие примеров, которые ты можешь постоянно прокручивать в голове при чтении.
Ошибка, пи не равно 3.1415926 как ты поймешь что имеется ввиду в учебнике, если ты не понимаешь о чем там пишется.
Ну вот как бы ты представил себе что такое число авогадро, точнее, как именно его вывели, если бы тебе его тупо дали?
Попробуй тогда рыбникова.
Двачую годноту. Был для меня глотком свежего воздуха в свое время.
Я лучше почитаю красивые и приятные книжки, чем каких-то нонеймов из сомнительных кругов.
>Какие тогда учебники стандартные?
Которые обычно рекомендуют начинающим изучение анализа: Тао, Зорич, Рудин, Фихтенгольц, Смирнов, etc.; но, вообще, это условность, конечно.
>И у этой функции нету ни одного из трех перечисленных пунктов в точке ноля.
Так и есть. Кто-то утверждал другое?
>И потом, ты же сам пишешь что предел выходит из непрерывности.
Есть небольшая разница между влечением и определением. Непрерывность влечёт существование предела, но определить их можно разными способами: можно — независимо друг от друга, можно — непрерывность через предел, а можно — предел через непрерывность. В большинстве курсов используют первые два способа, поэтому можно считать, что это общепринято, хотя и не значит, что правильно.
>я все-равно буду упарываться тем, что нравится, что красиво.
Могу пожелать только удачи.
>как ты поймешь что имеется ввиду в учебнике, если ты не понимаешь о чем там пишется.
Моё замечание относилось больше к чтению теорем, чем к чтению учебника в целом. Теоремы нужно читать «нисходяще» (но и разделы тоже можно таким образом читать), а после того, как прочитал раздел, параграф, главу, etc., необходимо делать обзор пройденного, краткое резюме: что ты прочитал, какие теоремы прошёл, чему научился.
>Рудин
))))))))00
>Зорич
Ненавижу его. Не знаю почему. Просто бесит.
>Фихтенгольц
Видел, как трехтомный курс фихта толкали за 5200 деревянных.
Ебать.
Тексту уже лет 50 или больше, а пипл хавает, барыги наживаются.
)))
>>Рудин
>))))))))00
Этот-то чем тебе не угодил?
Ничем. Просто книга не для человека, который даже калькулюс в глаза не видел.
Если человек не видел даже калькулюс в глаза, то можно почитать книги по анализу для школьников. Ты сам, какой учебник порекомендуешь? Какой тебе понравился? По какому учишься?
>можно — независимо друг от друга, можно — непрерывность через предел, а можно — предел через непрерывность.
Но резоннее выразить все через непрерывность, чтобы потом в тензорный анализ, топологию и пучки с расслоениями вкатываться на основе определения дифференциала/основного линейного приращения
Ад какой.
Но все-равно спасибо!
Помогите с уравнением, не знаю что дальше делать:
log2(9-2x) = 10lg(3-x)
Применил логарифмическое свойство, а дальше что делать?
log2(9-2x) = (3-х)
log2(9-2x) = 10lg(3-x)
Применил логарифмическое свойство, а дальше что делать?
log2(9-2x) = (3-х)
log2(9-2x)=log223-x
9-2x=23-x
Звиздец, конечно, читать на англ, очень не привычно. Это мне не книжки по си или пистону. Хотя и там ыли трудности, но здесь они больнее бьют по пониманию. Надо грамматику задрочить, иначе пиздец.
Это хорошо, если трудно. Учишься значит. Когда всё легко идёт, то ты по сути ничего нового не узнаёшь.
Точнее количественно может и узнаёшь, но качественно не развиваешься.
Типа, больно значит живой? Охохо. Вообще, спасает что книжка легкая, иначе вообще бы сдулся.
И как я не додумался до такой элементарщины? Как удалить свои посты?
Забыл поблагодарить. Благодарствую, анон.
Иронично, что теорему все же доказали в 1994 году. Всего-то через 22 года.
Еще годные фильмецы от этого режиссера
"Что такое теория относительности" и
"Физика в половине десятого"
Никак решивший посмотрел фильм и таки продал душу.
Смотрел недавно, да. Чертовски атмосферные такие себе рассказы получаются у режжисера
Раз уж охуительных историй тред, то я своевольно присовокуплю к историям цитаты.
"Я в детстве все время этим занимался. Рисовал длинный-длинный натуральный ряд и долго-долго на него смотрел"
Савватеев А.В
"Я в детстве все время этим занимался. Рисовал длинный-длинный натуральный ряд и долго-долго на него смотрел"
Савватеев А.В
Мне нравится его история о том, как учитель дал им задание про совершенные числа, и там под тремя звёздочками было доказать, что нечётных совершенных чисел нет. Я вот тоже после того, как услышал две тетради по 48 листов исписал, кажется ну вот же, очевидно, а потом копаешь, а там облом. И так, и сяк, а по итогу никак. Но больше всего позабавил подход учителя, конечно.
А вообще, раз уж такой разговор пошёл, кто-нибудь пробовал применять гомологическую алгебру к теории чисел, если пробовал хотелось бы что-то почитать по этому поводу.
Просто, например, у Ромы Михайлова есть такая концепция "глубинный узор с разрывом", ну это художественное название, к сожалению моей подготовки не хватает, чтобы грамотно записать то, что он как математик имеет ввиду, но суть в том, что у этой штуки есть некоторые свойства, некоторое поведение, которое очень напоминает то, как простые числа проявляются в натурально м ряду. Было бы круто прокачаться в теории чисел и ГАМАЛОГИЯХТАПАЛОГИЯХ и проверить теорию о том, что натуральный ряд это и есть такой узор с разрывами на месте простых. Прямо вот сильное, интуитивное ощущение, что там есть связь. Но я слишком нуб что там, что там.
Вспомнил что год назад, когда я еще не заинтересовался математикой, случайно глянул видео какого-то бородача-иностранца про математику, помню что он разговаривал специально тихокакая то аббревиатура из четырех букв английских мелькала..забыл вообще. Хотел снова найти, чтоб в подписках висел..
Может у кого завалялся случайно ответ
Может у кого завалялся случайно ответ
Здорова, пидоры.
Я теперь SJW-активист.
Я теперь SJW-активист.
Смотрю, у вас тут уныло совсем без меня.
Сотона, ну соснул ты с теоремой Ферма, ну бывает, зачем же так гореть? Хочешь я тебе душу продам, а ты гипотезу Римана докажешь?
Может, там подсказка в фильме где-то.
Вот, например, заставка. Там берется корень из чёрта. К чему бы это? Надо расследовать
Решение гипотезы Римана вполне может быть заключено в квантовых точках. Смотри туда.
Как бы там ни было, нужен слишком неординарный подход. Вряд ли эту гипотезу решит человек.
Сотона, я вижу ты подковался за это время, можешь что-то подсказать по этому вопросу?
>А вообще, раз уж такой разговор пошёл, кто-нибудь пробовал применять гомологическую алгебру к теории чисел, если пробовал хотелось бы что-то почитать по этому поводу.
Я и не думал, что ты более мерзким, но ты стал. Не было человека, гадостней тебя на этой доске и не будет.
У Ромы я спрашивал, он сказал "без понятия, я числа плохо понимаю".
Черт предложил использовать непрерывные дроби.
Через непрерывные дроби о черта можно запарафинится, это путь вникуда
Гугли триангулированные категории. Гомо-категория в stable infinity-category (со спектрой), например.
Если что, у Бурбаки есть по спектральным последовательностям.
БЛЯЯЯЯЯЯЯЯЯЯЯЯЯЯДЬ!!!!!!!!! СУКА!!!!! ПИДАРАС!!! ПАЛКУ, ПАЛКУ ДАВАЙ!!!!! ПАЛКУ ДАВАЙ БЛЯДЬ!!!!!!
На английском вообще-то всё _может_ почему-то проще даваться, если длительное время себя заставлять читать тексты со многосложными синтаксическими конструкциями, ориентироваться на речь, где много чего объясняют и делают это с большим количеством сравнений. А потом видишь уже эти слова, видишь ключевые фразы, эти сравнения вживляются в голову и ты видишь значения, связи между словами. И сам словарный запас тоже растёт. Но да, ты прав, грамматику нужно тоже подтягивать. А еще читай побольше, просто читай.
Кстати, моя биткоин-ферма сгорела. Деньги кончились за месяц.
Теперь устроился грузчиком.
Теперь устроился грузчиком.
А как твой мозг, разрушенный наркотиками? Почему ты до сих пор жив?
Эрдёш всю жизнь на спидах сидел, например. Без них не мог в математику. Так что такое себе обвинение.
Разгадка проста. Я практички сверхчеловек. На пути к нему. Но могу и умереть, да.
Но я не то что говорить, я об этом не имею права даже молчать.
Ты давал какой-то тест для прохождения мне. Забыл таки. Дай ещё раз.
Не, с Вхореном случай клинический. У него мозг разъёбан просто.
Больше всего хлопот доставила ему инструкция о том, как вербовать среди местного населения платных доносчиков и осведомителей. Придя к заключению, что невозможно завербовать кого-нибудь оттуда, где начинается Анонимность, потому что там весь народ честный, он наконец решил взять к себе на службу деревенского подпаска по прозванию Великий Пучкни. Это был кретин, который всегда пучкал, услыхав свою кличку, несчастное, обиженное природой и людьми существо, калека, за 15 рублей в год и за жалкие харчки трипкодил в /math.
Модульный дед велел его призвать и сказал ему: - Знаешь, Хорен, кто такой "Гротендик"?
- ПУЧК!
- Не пучкай. Запомни: так называют величайшего математика. Знаешь, что такое алгебраическая геометрия?
- Пучк. Вроте дик! Аналитическая говнометрия.
- Молодец, Хорен. Так запомни: если услышишь, когда ходишь по избам обедать, кто-нибудь скажет, что Гротендик скотина или что-нибудь в этом роде, то моментально приди ко мне и сообщи. За это получишь от меня пару биткоинов. А если услышишь, как кто-нибудь скажет, будто кто-то хвалит вторую культуру, опять приходи ко мне, понимаешь? Скажешь, кто это говорил, и снова получишь двадцать биткоинов. Но если я узнаю, что ты что-нибудь скрыл,-- плохо тебе придется. Заберу и отправлю в Писек. А теперь, ну-ка, Хорен, пучкни!
Хорен пучкнул, а Дед дал ему сорок биткоинов и, довольный собой, написал репорт моче, что завербовал осведомителя.
На следующий день к деду пришел вербит и сообщил ему по секрету, что утром он встретил за деревней сельского дурачка Хорен-Пучкни и тот ему сказал: "Вербит, а дед говорит, что Гротендик второкультурщи ПУЧК ПУЧК ПУЧК" После дальнейшего разговора с вербитом дед велел арестовать сельского петуха. Позднее градчанский суд приговорил его к годовому бану. Он был обвинен в опасных и предательских злодеяниях, в подстрекательстве, оскорблении Гротендика и в целом ряде других преступлений и проступков.
Хорен-Пучкни на суде держал себя, как на двачев, на все вопросы блеял козой, а после вынесения приговора крикнул: "Пучк"-- и прыгнул. За это он был наказан в дисциплинарном порядке: жесткая постель, одиночка и три дня в неделю на картофан и водку.
С тех пор у деда не было осведомителя, и ему пришлось ограничиться тем, что он сам выдумывал себе осведомителя, сообщил по инстанции вымышленное имя и таким образом повысил свой ежемесячный заработок на пятьдесят биткоинов, которые он пропивал в трактире dxdy. После десятой кружки его начинали мучить угрызения совести, пиво казалось горьким, и он слышал от крестьян всегда одну и ту же фразу: "Что-то нынче наш дед невеселый, словно как не в своей тарелке". Тогда он уходил домой, а. после его ухода кто-нибудь всегда говорил: "Видать, наши во Франции опять обделались - дед сегодня больно молчаливый"
По крайней мере он мне подсказал куда копать по моему вопросу, видно, что искушённый.
Слушай, а ты уверен в его компетенции? Он же даже определение модуля сказать не может.
Глянь-ка на это. Ему уже не помочь.
>Слушай, а ты уверен в его компетенции?
Ну он мне сказал гуглить, я загуглил , просмотрел, ща чай заварится попью, затем залью на читалку и буду читать. Походу как раз то, что я имел ввиду.
http://www.dissercat.com/content/triangulirovannye-kategorii-v-kommutativnoi-i-nekommutativnoi-geometrii
> Он же даже определение модуля сказать не может.
Ну Рома Михайлов тоже чисел не понимает, как он сказал. Чем сильнее математик в своей области, тем меньше он знает остальные, логично так-то. Как он писал:
>Душман начинал обучение над теми, кто к нему приходил, с определенной эстетики. Это касалось одежды, походки, даже музыкальных вкусов. Он так чутко и эмоционально объяснял, какая фигура красива, а какая нет, что это гладко входило в восприятие и никакого сопротивления не встречало. Например. Надо носить широкую одежду, в которой удобно двигаться, чтобы в случае драки она не стесняла движений. Нельзя носить шорты - в этом он и цыгане были достаточно категоричны, ибо для мужчины показывать ноги окружающим - позор. Купаться можно в таких боксерских штанах по колено, но ни в коем случае не в плавках. Но главное! Он объяснял, что сила заключается в тех умениях и пониманиях, которых ни у кого вокруг больше нет. Он обсмеивал понятия "гармоничное развитие", "идеальная фигура", объяснял, что если у человека идеальная фигура, как у качков в телевизоре, с ним можно справиться за несколько секунд, уничтожив нестандартным ударом, который порвет связки. А если у тебя всесторонне развитие, это означает, что у тебя мозг во все стороны распухает, и ты перестаешь понимать даже простейшее. Дело даже не в том, насколько адекватно было его восприятие, а в том, как он это подавал.
>Глянь-ка на это. Ему уже не помочь.
И опять у Ромы:
>Душман объяснял, что мир держится на маргиналах, на хохочущих чесунчиках, на завывающих уродцах, а не на умствующих эрудитах.
Я не фанат Ромы, ничего такого, но он охуенен и я с ним согласен в этом, конечно, есть исключения, но вдруг Хорен из таких? Мне не хочется строить из себя умника и смеяться над ним только потому, что он не знает какого-то определения.
Забавно, как меня разделили на Хорена и "деда". Я думал, что ясно, что это один человек.
Хотя. Мы же все тут один человек. Нет? В клетке.
>умствующих эрудитах
>всесторонне развитие
Хотя всю свою жизнь я дрочил на это, и вот только встретив Рому и его тексты стал задумываться. Может я шёл не туда.
Про модули - это у них мем такой. Просто сами не знают, насколько это определение лёгкое.
Как я понял, кто-то создал вики, назвал ее "Модуль над кольцом" и на вопрос, что такое модуль, промолчал. Отсюда и пошло.
Я тут недавно, не застал ваших войн, хотя мем про ПУЧКиста заценил, годно, ёмко и вообще. Сам с ними столкнулся недавно.
> Я думал, что ясно, что это один человек.
Нет. Не смей приписывать его заслуги себе.
Лживая мразь, это ты на своём форуме промолчал, когда тебе анон задал вопрос.
Просто не верь ему наслово, хорошо. Он лживый подхалим, который чуть не привёл эту доску к смерти. Серьёзно, этот петуч столько нам нагадил на доске, что нисчесть.
И да Хорен и есть такой вот пучкист, причём в терминальной стадии.
>Просто не верь ему наслово, хорошо.
Хорошо, я обычно на слово никому не верю, прошу пруфы как дотошный уёбок, если мне что-то не ясно в словах собеседника. Просто хотел бы отметить, что конкретно сегодня конкретным постом он мне помог,так что у меня нет оснований сомневаться в его компетенции. Остальное в том посте лирика, к размышлению и вообще, просто вспомнил в тему диалога.
Ну может быть, я не знаю, за пределы этого треда не выхожу.
Приятно знать и видеть, что не только у меня проблемы с головой.
Ради этого сюда можно заходить. Я не одинок.
Моча обещала забанить эту макаку на год
Игнорируйте его, репортите и просто скрывайте посты
Если хотите выговориться, то вам сюда
https://2ch.hk/d/res/445826.html
Игнорируйте его, репортите и просто скрывайте посты
Если хотите выговориться, то вам сюда
https://2ch.hk/d/res/445826.html
Бамп, ну.
Куранта почитай. Он легко читается и можешь интуицию на нём нарабатывать.
>
Класс. Будто сам Ромич, ебать его, харе Кришна, снизошёл в /матх/ и соблаговолил тут просраться.
У Ромича нет такой тяги к некрофилии и разрушению, как у вхорена. Хорен всё ломает на своём пути, Ромич создаёт. Между ними есть огромная разница.
Слушай, тут один анон пытался доказать мне, что единиц на самом деле несколько, единица из R, Q, С, N это всё разные единицы. Он говорил, что с точки зрения формального метода это так. Ещё он говорил что-то вроде операнды и операторы это одно и то же, что математика в рот ебала смысл и это суть значки и правила действий над ними. Типа от рисования каракуль на песке это не отличается. Я тогда сказал, что Евклид бы ему ебальничек-то расквасил за такую хуйню. Что ты думаешь по этому поводу? Мне кажется, что формальная логика такой раздел, к которому стоит приступать уже хорошо подготовившись иначе есть риск неверно понять написанное и пиздануться на всю голову.
Интересно твоё мнение.
Рома гений и философ. правда трус немножко, но кто не трус пусть первый бросит в него камень
>единица из R, Q, С, N это всё разные единицы
По сути да, но по факту различие между ними как между хуем васи и хуем пети.
>гений
В смысле математики. Убеждён, что многие из того, чем он занимается, может иметь самое разное применение в самых разных областях математики, когда-нибудь я прокачаю ГАМАЛОГИИТАПАЛОГИИ и смогу применять fr язык для нахождения ответов на вопросы, ебущие меня всю жизнь.
Ну вот, я примерно так и подумал. Всё же хуй есть хуй, а не пизда.
Может быть здесь есть понаехавшие учиться в НМУ из Украины? Расскажите истории успеха.
Почему трус и в чём его гениальность? Я серьёзно не очень в курсе его достижений, кроме меметичных лекций и малопонятных загонов. Для меня он скорее забавный человек-мем и мистический танцующий математик.
У него есть почетное звание "Профессор РАН". Как минимум круто.
>и в чём его гениальность?
Это лично моё мнение, кажется, что он в своих работах вскрыл какой-то фундаментальный принцип. Вот этот глубинный узор с разрывами, есть много вещей, ведущих себя так же, это и натуральный ряд с простыми, и шредингеровская эволюция с внезапной редукцией квантового состояний
Скачок квантового состояния^22Л^ в одно из собственных состояний оператора Q
представляет собой процесс, именуемый редукцией вектора состояния или коллапсом волновой
функции. Это одна из наиболее загадочных черт квантовой теории, и в этой книге мы не
раз будем возвращаться к этому понятию. Мне представляется, что большинство физиков,
занимающихся квантовой теорией, не считают редукцию вектора состояния реальным
явлением физического мира, но это лишь отражает тот факт, что мы не считаем, будто вектор
состояния действительно описывает физическую реальность на квантовом уровне. К этому
спорному вопросу мы вернемся подробнее в главе 29. Тем не менее безотносительно к
тому, какой позиции мы придерживаемся относительно физической реальности этого явления,
при практическом применении квантовой механики мы должны считать, что состояние
действительно совершает подобный скачок всякий раз, когда производится измерение. Сразу
после измерения опять восстанавливается шредингеровская эволюция, пока над системой
не производится следующее измерение, и так далее.
Я буду обозначать шредингеровскую эволюцию буквой U, а редукцию состояния —
буквой R. Чередование этих двух совершенно различных процессов должно
проявляться в весьма необычном поведении Вселенной! (См. рис. 22.1). Можно предположить, что
в действительности это есть приближенное описание чего-то пока не известного. Может
быть, существует некоторое более общее математическое уравнение или некоторый
принцип эволюции когерентного типа, по отношению к которому U и R являются предельными
случаями? Мое собственное мнение состоит в том, что подобная модификация квантовой
теории вполне возможна, и она может составить часть новой физики XXI века;
и сознание, и социум и хуй знает что ещё. Везде там на определённом этапе возникают проблемы, невозможность детерминированно рассуждать, возрастающая сложность, потому многие из этих областей сейчас любопытные, но не более, на практике не особо применимы, например есть концепт хаотической нейросети, но из-за упомянутой невозможности предсказать работу, управлять и просчитывать это бесполезная хуита на практике. Много областей, в каждой из которых висит здоровый замок, пишут мол математика пока не имеет методов и тому подобное. Так вот, очень похоже(а одно из свойств этого условного "узора с разрывами" невозможность его имитации, иными словами если что-то ведёт себя как такой узор, это скорее всего и есть такой узор), что у Ромы есть ключ. Но это всё имхо, ты понел, а так он как минимум один из сильнейших специалистов в своей области. На первую часть отвечать не хочу, так как не хочу бросать тень и всё такое, считай, что это вскукарек безпруфный.
Сап, двач. Что с гипотезой Коллатца? Её доказали или нет?
Смотрите что нашёл: https://lenta.ru/news/2011/06/06/collatz/
http://mathhelpplanet.com/viewtopic.php?f=51&t=38152
> есть ключ
>Сколько можно получить предложений следующего поколения из одного данного предложения - только одно, или несколько тоже можно?
>только одно - начальное предложение задает бесконечный текст
>пока никак, берем любое, мы сейчас чисто играем в эти fr-тексты, пытаясь анализировать то, что получается. Глобально - это функториальный универсум, со множеством внутренних связок. Мы хотим понять, из чего он состоит и что сообщает.
Он недавно сделал статью по fr-языку, пока они там сами толком не знают, что с этим делать, играются, исследуют, но в теории это может стать фундаментом для аппарата, способного решать самые разные проблемы. Насколько я понял это что-то вроде, ну вот есть дифференциальное уравнение, рекуррентное соотношение, это что-то вроде того, только тут на каждом шаге появляется не число, а новое уравнение такого типа. Короче это всё охуеть как интересно и мало что из этого понятно, но даже то, что понятно приводит в восторг.
Первая статья
https://arxiv.org/pdf/1510.09044.pdf,
Примеры применения
https://arxiv.org/pdf/1611.01313.pdf,
https://arxiv.org/pdf/1605.08196.pdf
Пройден.
Аноны, кому не лень, распишите детально что проходят на первых 2-3х курсах вуза по матану (названия на сайтах для меня ничего не говорят). Я сам учусь за бугром, и было бы интересно сравнить программу.
Сначала ты. А то вдруг ты шпиён, информацию получишь и больше тебя никто не видел.
Есть что-то типа Wolfram Alpha, но чтобы показывало ход решения?
>И да Хорен и есть такой вот пучкист, причём в терминальной стадии.
Да, ты был прав.
Ладно, за первые 2 курса (потом дропнул тк не мой профиль, сам изучаю химию, а матан взял для интереса) мы прошли диффуры 2 порядка, теорему моавра и множественные корни единицы, полярные координаты,гиперболические синусы/косинусы, матрицы, ряды тэйлора, 3Д вектора и все с ними связанное, механика , много статистики и алгебра логики
Курс куранта прочитай.
Какое направление математики на курсе? Что раздрачивают?
Одно известно точно: после диплома винегрет он будет готовить отлично.
Бесполезное говно.
Этот доп матан на 2 курса берут будущие ученые, вот там и намешано разного (механика для физиков и инженеров, статистики много для ученых, остальное для общего развития). Еще раз скажу что это не профиль, у тех кто собирается брать бакалавра по матану все намного хардкорней
Покакал на тебя твоим любимым героином.
Ну направление в каком изучают математику есть? Или ты там тупо всю математику, от тригонометрии до кардиналов, от дробей до зфц теории учишь?
Я уже чувствую себя гебефреником, епта, от этого всего. Что делать?
что делать если хочется читать фихтенгольца а надо читать зорича
Читай сначала Фихтенгольца, а потом Зорича и привязывай Зорича к Фихтенгольцу.
Первый курс
Анализ на $R^n$. Дифференциал отображения. лемма о сжимающем отображении. Теорема о неявной функции. Интеграл Римана и Лебега. ("Анализ" Лорана Шварца, "Анализ" Зорича, "Задачи и теоремы из функ. анализа" Кириллова-Гвишиани)
Гильбертовы пространства, банаховы пространства (определение). Существование базиса в гильбертовом пространстве. Непрерывные и разрывные линейные операторы. Критерии непрерывности. Примеры компактных операторов. ("Анализ" Лорана Шварца, "Анализ" Зорича, "Задачи и теоремы из функ. анализа" Кириллова-Гвишиани)
Гладкие многообразия, субмерсии, иммерсии, теорема Сарда. Разбиение единицы. Дифференциальная топология (Милнор-Уоллес). Трансверсальность. Степень отображения как топологический инвариант.
Дифференциальные формы, оператор де Рама, теорема Стокса, уравнение Максвелла электромагнитного поля. Теорема Гаусса-Остроградского как частный пример.
Комплексный анализ одного переменного (по книге Анри Картана либо первому тому Шабата). Контурные интегралы, формула Коши, теорема Римана об отображениях из любого односвязного подмножества $C$ в круг, теорема о продолжении границ, теорема Пикара о достижении целой функцией всех значений, кроме трех. Многолистные функции (на примере логарифма).
Теория категорий, определение, функторы, эквивалентности, сопряженные функторы (Маклэйн, Categories for working mathematician, Гельфанд-Манин, первая глава).
Группы и алгебры Ли. Группы Ли. Алгебры Ли как их линеаризации. Универсальная обертывающая алгебра, теорема Пуанкаре-Биркгоффа-Витта. Свободные алгебры Ли. Ряд Кэмпбелла-Хаусдорфа и построение группы Ли по ее алгебре (желтый Серр, первая половина).
Второй курс
Алгебраическая топология (Фукс-Фоменко). Когомологии (симплициальные, сингулярные, де Рама), их эквивалентность, двойственность Пуанкаре, гомотопические группы. Размерность. Расслоения (в смысле Серра), спектральные последовательности (Мищенко, "Векторные расслоения..."). Вычисление когомологий классических групп Ли и проективного пространства.
Векторные расслоения, связность, формула Гаусса-Бонне, классы Эйлера, Черна, Понтрягина, Штифеля-Уитни. Мультипликативность характера Черна. Классифицирующие пространства ("Характеристические Классы", Милнор и Сташеф).
Дифференциальная геометрия. Связность Леви-Чивита, кривизна, алгебраическое и дифференциальное тождество Бьянки. Поля Киллинга. Кривизна Гаусса двумерного риманова многообразия. Клеточное разбиение пространства петель в терминах геодезических. Теория Морса на пространстве петель (по книге Милнора "Теория Морса" и Артура Бессе "Эйнштейновы Многообразия"). Главные расслоения и связности в них.
Коммутативная алгебра (Атья-Макдональд). Нетеровы кольца, размерность Крулля, лемма Накаямы, адическое пополнение, целозамкнутость, кольца дискретного нормирования. Плоские модули, локальный критерий плоскости.
Начала алгебраической геометрии. (первая глава Хартсхорна либо Шафаревич либо зеленый Мамфорд). Афинное многообразие, проективное многообразие, проективный морфизм, образ проективного многообразия проективен (через результанты). Пучки. Топология Зариского. Алгебраическое многообразие как окольцованное пространство. Теорема Гильберта о нулях. Спектр кольца.
Начала гомологической алгебры. Группы Ext, Tor для модулей над кольцом, резольвенты, проективные и инъективные модули (Атья-Макдональд). Построение инъективных модулей. Двойственность Гротендика (по книжке Springer Lecture Notes in Math, Grothendieck Duality, номера примерно 21 и 40).
Теория чисел; локальные и глобальные поля, дискриминант, норма, группа классов идеалов (синяя книжка Касселса и Фрелиха).
Редуктивные группы, системы корней, представления полупростых групп, веса, форма Киллинга. Группы, порожденные отражениями, их классификация. Когомологии алгебр Ли. Вычисление когомологий в терминах инвариантных форм. Сингулярные когомологии компактной группы Ли и когомологии ее алгебры. Инварианты классических групп Ли. (желтый Серр, вторая половина; Герман Вейль, "Инварианты классических групп"). Конструкции специальных групп Ли. Алгебры Хопфа. Квантовые группы (определение).
Третий курс
К-теория как когомологический функтор, периодичность Ботта, алгебры Клиффорда. Спиноры (книжка Атьи "К-Теория" либо А.С.Мищенко "Векторые расслоения и их применение"). Спектры. Пространства Эйленберга-Маклейна. Бесконечнократные пространства петель (по книжке Свитцера либо желтой книжке Адамса либо Адамса "Lectures on generalized cohmology", 1972).
Дифференциальные операторы, псевдодифференциальные операторы, символ, эллиптические операторы. Свойства оператора Лапласа. Самосопряженные операторы с дискретным спектром. Оператор Грина и приложения к теории Ходжа на римановых многообразиях. Квантовая механика. (книжка Р.Уэллса по анализу либо Мищенко "Векторые расслоения и их применение").
Формула индекса (Атья-Ботт-Патоди, Мищенко), формула Римана-Роха. Дзета-функция оператора с дискретным спектром и ее асимптотики.
Гомологическая алгебра (Гельфанд-Манин, все главы проме последней). Когомологии пучков, производные категории, триангулированные категории, производный функтор, спектральная последовательность бикомплекса. Композиция триангулированных функторов и соответствующая спектральная последовательность. Двойственность Вердье. Формализм шести функторов и превратные пучки.
Схемная алгебраическая геометрия, схемы над кольцом, проективные спектры, производные функции, двойственность Серра, когерентные пучки, замена базы. Собственные и отделимые схемы, валюативный критерий собственности и отделимости (Хартсхорн). Функторы, представимость, пространства модулей. Прямые и обратные образы пучков, высшие прямые образы. При собственном отображении высшие прямые образы когерентны.
Когомологические методы в алгебраической геометрии, полунепрерывность когомологий, теорема Зариского о связности, теорема Штейна о разложении.
Кэлеровы многообразия, теорема Лефшеца, теория Ходжа, соотношения Кодаиры, свойства оператора Лапласа (нулевая глава главы Гриффитса-Харриса, понятно изложена в книжке Андре Вейля "Кэлеровы многообразия"). Эрмитовы расслоения. Линейные расслоения и их кривизна. Линейные расслоения с положительной кривизной. Теорема Кодаиры-Накано о занулении когомологий (Гриффитс-Харрис).
Голономии, теорема Амброза-Зингера, специальные голономии, классификация голономий, многообразия Калаби-Яу, гиперкэлеровы, теорема Калаби-Яу.
Спиноры на многообразии, оператор Дирака, кривизна Риччи, формула Вейценбека-Лихнеровича, теорема Бохнера. Теорема Богомолова о разложении многообразий с нулевым каноническим классом (Артур Бессе, "Эйнштейновы многообразия").
Когомологии Тэйта и теория полей классов (Касселс-Фрелих, синяя книжка). Вычисление фактора группы Галуа числового поля по коммутанту. Группа Брауэра и ее приложения.
Эргодическая теория. Эргодичность бильярдов.
Комплексные кривые, псевдоконформные отображения, пространства Тейхмюллера, теория Альфорса-Берса (по книжке Альфорса тоненькой).
Толсто.
мат спецуха?
или курс матана?
в душе не ебу, наверное калькулюс дрочат под картофан
Первый семестр.
1. Введение в теорию множеств.
Множество. Формула, логические операции с формулами. Предикат, аксиома выделения. Операции со множествами и их связь с логическими операциями: объединение, пересечение, разность. Упорядоченная пара, декартово произведение двух множеств. Бинарное отношение - рефлексивное, симметричное, транзитивное, антирефлексивное. Функциональное отношение, отображение. Сюръекция, инъекция, биекция. Алгебраическая структура, идея об изоморфизме структур. Отношение эквивалентности, фактормножество. Отношение порядка, частично/линейно упорядоченное множество. Максимум, минимум, наибольший и наименьший элементы. Полный порядок, лемма Цорна. Идея формального метода. Натуральные числа, принцип математической индукции. Сочетания, размещения, перестановки, биномиальные коэффициенты.
2. Вещественные и комплексные числа.
Аксиомы упорядоченного поля. Супремум, инфимум, аксиома непрерывности. Аксиоматическое определение R. Сечение Дедекинда в области рациональных чисел, операции над сечениями. Несобственные сечения, расширенная прямая. Иррациональные и рациональные сечения. Теорема о непрерывности R, сечения Дедекинда как модель R. Бесконечные десятичные дроби, несчетность R. Комплексные числа как пары вещественных, операции с комплексными числами, формы записи комплексных чисел, теорема Муавра о корнях.
3. Метрическая топология.
Норма, метрика. Стандартные метрики на R и R^n. Метрическое топологическое векторное пространство. Открытое, замкнутое множества. Последовательность, бесконечно малая последовательность, предел последовательности, единственность предела. Предельная точка, теорема Больцано об ограниченном бесконечном числовом множестве, замыкание. Операции над последовательностями. Связь предела с операциями, с порядком, теорема о милиционерах. Лемма о вложенных отрезках, лемма Бореля-Лебега. Фундаментальная последовательность, критерий Коши для последовательностей. Полное пространство, пополнение. R как фактормножество фундаментальных последовательностей рациональных чисел. Ряд, сумма ряда, абсолютно сходящиеся ряды, необходимый признак сходимости, признак сравнения, признак Даламбера, знакопеременные ряды, признак Лейбница, кратные ряды. Определение элементарных функций. Неравенства Бернулли, Гельдера, Иенсена, Коши-Буняковского-Шварца, Минковского.
4. Общая топология, её связь с метрической.
Абстрактные топологические пространства. Хаусдорфовы пространства. База, предбаза, лемма Александера, теорема Тихонова. Индуцированная топология. Метризуемое пространство. Открытые отображения, гомеоморфизмы. Компакты. Одноточечная компактификация Александрова, топология на N. Компактность в R^n, критерий компактности. Совершенные множества, совершенные подмножества R^n. Канторово множество. Связное пространство.
5. Непрерывность.
Непрерывные функции топологических/метрических пространств, предел функции, единственность предела. Критерий Коши для функций. Операции над отображениями топологических векторных пространств, перестановочность их с пределом. Непрерывные отображения компактов. Равномерная непрерывность, теорема Кантора. Непрерывность и связность. Принцип сжимающих отображений. Разрывы, их классификация. Особенности функций из R в R. Бесконечно-малые, таблица эквивалентных бесконечно-малых. Определение предела по Гейне. Эпсилон-дельта формализм.
6. Дифференцирование.
Производная, дифференциал. Производная вещественнозначной функции. Арифметические операции и производная, производная композиции. Производные элементарных функций. Теоремы Ферма, Ролля, Коши и Лагранжа. Правило Лопиталя. Производные высших порядков. Теорема Тейлора, ряды Маклорена. Алгоритм исследования функции. Сходимость в C, ряды с комплексными членами, формула Эйлера, алгебраическая замкнутость C.
Второй семестр.
1. Неопределенный интеграл.
Первообразная, неопределенный интеграл. Таблица интегралов. Замена переменной, интегрирование по частям, возвратные интегралы, особенности интегрирования подклассов элементарных функций - рациональных, иррациональных, тригонометрических, etc. Дифференциальный бином, подстановки Эйлера.
2. Определенный интеграл.
Определение интеграла по Риману, класс интегрируемых функций. Интегральные суммы Дарбу, критерий Дарбу. Линейность, аддитивность, монотонность интеграла. Оценка интеграла, теоремы о среднем. Замена переменной, интегрирование по частям, формула Тейлора. Приложения интеграла. Площадь криволинейной трапеции, работа переменной силы, длина кривой, объём тела вращения. Несобственный интеграл, особенности несобственного интеграла.
3. Элементы теории меры.
Координатные брусы. Мера, пространство с мерой, задача о продолжении меры, алгебра измеримых множеств. Внешняя мера, лемма Валле-Пуссена, сигма-алгебра продолжение меры. Теорема Каратеодори для брусов. Мера Жордана. Мера Лебега, измеримые по Лебегу множества. Измеримые функции, измеримость композиции.
4. Интеграл Лебега.
Верхние и нижние суммы Лебега, интеграл. Класс интегрируемых функций. Линейность, счетная аддитивность и другие свойства интеграла Лебега. Теорема об интегрируемости непрерывных функций, общая формула Ньютона-Лейбница.
5. Функциональные последовательности и ряды.
Сходимость почти всюду. Сходимость по мере. Предел монотонной последовательности множеств. Предельный переход под интегралом. Интегрирование и дифференцирование рядов, степенные ряды, теорема Абеля, область сходимости. Признаки сходимости. Аналитические функции. Доказательство существования элементарных функций.
6. Дифференцирование многих переменных.
Производная по направлению, частные производные. Слабый и сильный дифференциал. Координаты дифференциала. Матрица Якоби. Дифференциал композиции, дифференциал обратной функции. Теорема о среднем. Достаточное условие дифференцируемости. Частные производные высшего порядка. Общая формула Тейлора. Экстремумы функции многих переменных. Теорема о неявной функции. Теорема об обратной функции. Локальное приведение гладкого отображения к каноническому виду. Локальное разложение диффеоморфизма. Лемма Морса. Поверхность в R^n. Касательное пространство. Условный экстремум.
7. Кратные интегралы.
Сведение кратного интеграла к повторному. Теорема Фубини. Замена переменных в несобственном кратном интеграле. Несобственные кратные интегралы. Мажоритарный признак сходимости несобственного интеграла.
8. Дифференциальные формы.
Поверхность. Ориентация поверхности. Край. Площадь поверхности. Дифференциальная форма. Координаты дифференциальной формы. Внешний дифференциал. Формы на поверхностях. Интеграл от дифф.формы. по поверхности. Интегралы первого и второго рода. Форма объёма, её координаты. Симплексы и цепи. Теорема Стокса. Формулы Грина, Остроградского-Гаусса, Стокса. Поля, grad, rot, div. Потенциальные поля, векторный потенциал, точные и замкнутые формы. Классические уравнения теории поля.
Литература.
1. Фихтенгольц, "Основы математического анализа" и "Курс дифференциального и интегрального исчисления".
2. Зорич, "Математический анализ".
3. Рудин, "Основы математического анализа".
4. Дьедонне, "Основы современного анализа".
В реальной жизни изучить все перечисленное на первом же курсе не получается. Тем не менее, математические факультеты стараются. На непрофильных факультетах (например, у информатиков и физиков) заметная часть перечисленного опускается, причем информатики и физики опускают совершенно разные куски, оставляя кому что нужно.
Двачую этого.
Не увидел дискретки и теории чисел совсем.
Это матан. Дискретка - отдельный предмет.
В шары долблюсь.
>Бесконечно-малые
Нестандартный гомопидорский анализ или что?
Последовательность называется бесконечно-малой, если её предел равен нулю. Сумма конечного числа бм - бм, произведение бм на ограниченную - бм. Поскольку бм ограничена, произведение конечного числа бм снова бм.
Теорема. Число A является пределом последовательности x1, x2, x3, ... тогда и только тогда, когда существует бесконечно-малая последовательность y1, y2, y3, ... такая, что x1 = a+y1, x2 = A+y2, x3=A+y3, ...
Эта теорема и свойства бм автоматически дают арифметические свойства пределов последовательностей.
Для функций аналогично.
А анализ бесконечно-больших есть? Или он выводится из малых?
Это не "анализ бесконечно-больших", это просто пара фраз про бесконечно-большие. Да, есть.
>Да, есть.
Как называется?
"Таблица эквивалентных бесконечно-больших".
Через последовательности...
А как же тогда нестандартный анализ? Он же об этом самом, бесконечно малых.
Нет. Он про то, что всякое множество M с некоторой структурой (операции плюс отношения и константы) может быть погружено во множество M' с той же структурой, в котором есть по крайней мере один элемент, не получающийся из элементов множества M с помощью конечного количества применений операций в рассматриваемой структуре (такие элементы называются нестандартными). Это называется принцип идеализации. Про нестандартные элементы M' говорят просто, что они нестандартные элементы M.
Пример. Пусть x - нестандартный элемент множества натуральных чисел. Тогда x не получается никакой конечной последовательностью применений операций Пеано - т.е. x не является ни единицей, ни числом, получаемым прибавлением единицы к натуральному числу. Естественно считать (это ниоткуда не следует, высосем с потолка), что число x больше любого другого натурального числа.
Высасывание называется "принцип переноса".
Нестандартный анализ - это различной степени безумности попытки подогнать обоснуй под принцип идеализации и принцип переноса. Нестандартный анализ - это про тени чисел, про неклассические аксиоматики теории множеств. Это ехал ультрафильтр через ультрафильтр.
Конструктивист бы застрелился.
Это же тоже там же рассматривается, ну в стандартном матанализе, калькулюс или как-то так. Я про это говорил же, когда говорил, что он выводится из малых.
>это ниоткуда не следует, высосем с потолка
Но почему? Если x получается прибавлением к натуральному числу числа, отличного от единицы, то он явно больше любого натурального числа.
Так ведь НЕ получается.
Складывая между собой стандартные натуральные числа, можно получить лишь стандартные натуральные числа.
x может лежать где-то между 5 и 6, например.
Ну и что? Тогда будет 1,2,3,4,5,x,6,7,8,9,10,11..
Похоже твой пример неверен, написано, что нестандартный анализ имеет дело с более широким полем гипервещественных чисел, в котором не выполняется аксиома Архимеда. То есть эти числа всегда больше на какое-то число, чем максимальное натуральное число. Короче альтернативный способ работать с бесконечностями, заменяя их числами, как я понял.
Обычный средне-плохой курс, но можно. Фихтенгольца из литературы уберите только, не позорьтесь.
Поясни за Фихтенгольца. Ты его читал?
Я не он, но читал. Не понимаю хейта, хороший учебник, разве что большой.
Ты понял неправильно.
http://www.math.nsc.ru/LBRT/g2/english/ssk/infa.pdf - типичная книга по нестандартному анализу.
Значит это хуета какая-то.
Устаревший как по части изложения, так и по самому материалу.
Если не хотите испытать сгущение, читайте сразу Дьедонне по анализу.
Термин "точка сгущения" - общеизвестный. Ты давай по существу поясняй.
Ну арабские цифры тоже старые, давай теперь ноликами и единичками изъясняться
Открой его. Он начинает даже без теории множеств. Это пиздец, о чём говорить.
Анализ для новичка вообще должен излагаться на дифференциальных формах, как и изучение алгебры должно основываться с первых строк на языке категорий.
Планирую начать тихо писать лаконичный учебник с таким подходом по алгебре, кстати. Страниц в 150 максимум. Свободный к распространению, естественно.
>Планирую
Планируй. Вангую тебя на 10 страниц хватит.
Я даже набросал оглавление. Сюда не скину, конечно.
В отличие от тебя, я его читал. Поэтому на "это пиздец" ты меня не возьмёшь, говори по делу.
Что-то ты привираешь про множества.
Лул. Хайв.
2.1.7. Принцип идеализации: в каждом бесконечном множестве имеется
нестандартный элемент.
Адекватность приведенного положения общим представлениям о бесконечно-
сти несомненна. Принцип идеализации в дальнейшем часто дается в более силь-
ных формах, отражающих концепцию неисчерпаемого разнообразия идеальных
объектов. Например, иногда принимают, что все стандартные множества яв-
ляются элементами некоторого конечного множества. Число элементов такого
«универсального» множества колоссально и, что важнее всего, «недоступно» —
нестандартно. Поэтому не может вызывать удивление нестандартность самого
универсального множества.
Ну как хуета, там другие аксиомы, видимо. Но да, всё таки хуета. С чего это вдруг в бесконечном множестве натуральных чисел должны существовать какие-то нестандартные элементы? Только потому, что раз бесконечно, значит там всё что угодно может быть, такого плана логика? Не понимаю такого.
А ещё прикольно, что в книге, похоже, нет определения нестандартного элемента, на котором всё строится. Или я неправ, но пока что-то найти не могу.
Я говорю, что он не использует множества так, как должно, как современно.
А теория пределов у него вообще цирк. Пик.
>он не использует множества так, как должно, как современно
Как современно?
Оглавление не в счёт, на введение тебя не хватит. И да, если бы ты хоть что-то написал, то наверняка бы создал тред и скинул, ведь ты вниманиеблядь.
Это школьное доказательство, блядь. У Евклида было больше строгости, чем здесь.
Что не так?
Конкретики нет, я не вижу здесь нестрогости, если ты видишь укажи мне, чтобы посеять зерно сомнения.
>Иными словами, в нестандартном анализе предполагаются множествами те и
только те совокупности, которыми оперирует классическая — «стандартная» —
теория. Стоит подчеркнуть, что справедлива и переформулировка приведенно-
го утверждения: нестандартный анализ не считает множествами те и только те
совокупности, которые не признает в качестве множеств обычная математика.
Окей, но двумя страницами позже
>. Решающий новый момент, главная посылка, формирующая нестандарт-
ную теорию множеств, чрезвычайно проста. Она заключена в том, что множе-
ства бывают разные: стандартные и нестандартные
Налицо противоречие, нестандартный анализ официально зашквар. Мамку ебал автора.
Укажи на недостаток этого доказательства.
Курс рассчитан на школьников, если что.
>Это школьное доказательство, блядь. У Евклида было больше строгости, чем здесь.
>Конкретики нет, я не вижу здесь нестрогости, если ты видишь укажи мне, чтобы посеять зерно сомнения.
Ты не ответил на мой вопрос, Хорен. За слова надо отвечать.
>Раз Фихтенгольц в качестве школьного курса, а не университетского, то ладно. Тогда эта хуйня отчасти и допускается.
Я просто хочу внести ясность. Получается ты фуфломёт, пустой пиздабол, в системе ценностей которого беспруфные кукареки являются вполне допустимой моделью поведения, я правильно понимаю? Если так, то вопрос исчерпан. Дублирую твои ответы в этом треде, чтобы было понятно, с кем мы имеем честь тут разговаривать.
>максимальное натуральное число
Может любое выбранное?
Я хуй знает, я дальше стал вникать и охуел с этой параши еретической. Вся теория строится на нестандартных элементах, но определения нет его, написано что
> нестандартный анализ не считает множествами те и только те
совокупности, которые не признает в качестве множеств обычная математика.
А через две страницы вводятся нестандартные множества, которые блядь "обычная"(какая нахуй обычная? хуичная, блядь и это учебник говно блядь) математика не признаёт и, следовательно, не признаёт и нестандартный ебать его в рот анализ. Маму автора ебал, ещё раз говорю.
Так это у всей теории множеств вообще нету никаких примеров элементов множества.
Даже в качестве множества вещественных чисел не могут написать пример элемента множества. То же самое с сечениями дедекинда, никаких примеров ирациональных чисел. Хотя вру, корень из двух показывают и доказывают что он бесконечный.
Там дело не в том, а в противоречии внутри самой этой хуйни. Это же пиздец. Пусть тогда вводят собственное определение множества и прочей хуйни и тогда пожалуйста, а так ебитесь в рот, ваша книжкей можно только подтереться. По элементам множества ща поищу, не уверен.
>Объекты, из которых состоит множество, называют элементами множества или точками множества.
>характеризующие множество как совокупность различных элементов, мыслимое как единое целое
Ну да, сепульки какие-то. Но суть не в том, хотя это интересно, не знал, суть в том, что такое нестандартный элемент. Нет этого вообще. Ну хорошо, по аналогии элемент нестандартного множества. Но такое множество недопустимо, так как
> нестандартный анализ не считает множествами те и только те
совокупности, которые не признает в качестве множеств обычная математика.
Они изучают нихуя?
И что за "обычная" математика? Охуеть можно. Мегатрэш.
И потом, я, конечно, не уверен, но вроде бы у множества есть конкретное такое свойство: каждый элемент там должен быть в единственном экземпляре. Остальное уже мультимножество.
Правда я забыл, к чему я это, но это важно, да. Но забыл.
И да, ты на вопрос мне так и не ответил, фуфлыжник. Так что ты, скорее всего, примерно так же мыслишь, как авторы этой книжки. Обычная и необычная математика, противоречевая хуета в самой основе теории, это норма, чё. И так сойдёт. Страшно себе представить, что ты там за учебник высрешь, если высрешь когда-либо.
Теперь ты понял, почему прошаренные люди испытывают баттхерт, когда нестандартным анализом называют "ну тип тот же самый матан, только с актуальными инфинитезималями".
Теперь понял. Был невероятно неправ. Невероятно. Я так ещё никогда не ошибался, я обычно всегда по дефолту хорошо отношусь к людям, теориям и всему такому. С Хореном, кстати, тоже дичайше ошибся, может он и компетентен, но полнейший еблан. Опыт сын ошибок трудных, да.
О сколько нам открытий чудных
Готовят просвещенья дух
И опыт, сын ошибок трудных,
И гений, парадоксов друг,
И случай, бог изобретатель...
Хотя какая тут нахуй компетентность, совпадение скорее.
Судя по стилю письма это один человек.
>Munin писал(а):
Такое ощущение, что самое страшное в "элементарной математике" - это определения и доказательства. Невнятные, нестрогие, с пропущенными логическими шагами.
http://dxdy.ru/topic15081.html
Да и вообще таких совпадений не бывает, небось сам себя тут и пиарил, любитель вниманиеблядствовать.
Любой в итоге убеждается, что я прав.
У вас за всё время разве что Наполеоном не был. Или был.
Ща готовлюсь к экзам, и заметил, что в таких серьезных книгах как Ширяев или Феллер, ничего не сказано про геометрическую вероятность (ну или я так искал), а в книгах, где она упоминается, всегда идет заметка о том, что есть много подводных камней с заданием такой вероятностной меры. Раз так, то как без геометрической вероятности решить классическую задачу о встрече:
Вася с Машей договорились встретится в 15:00. Каждый из них приходит, ждет 20 минут и уходит, если никого не встретил. Каждый приходит в случайный промежуток часа. Какова вероятность встречи?
Вася с Машей договорились встретится в 15:00. Каждый из них приходит, ждет 20 минут и уходит, если никого не встретил. Каждый приходит в случайный промежуток часа. Какова вероятность встречи?
Моча потерла пост с ссылкой на d, но не потерла Хорена.
Это пиздец, теперь здесь параша официально
Сука, тупорылая гнида
Это пиздец, теперь здесь параша официально
Сука, тупорылая гнида
пока тут кудахчут и кукарекают, у меня подгорело от того, что знать и применять приложения анализа хочется ужепрямщас, но надо ещё долго ботать и прочитать хотя бы 3 книжки.
чет даже обидно немного. кто-то может долго и усидчиво ботать, невзирая на мирские соблазны, а я не очень, только если изолироваться как инок какой-нибудь
чет даже обидно немного. кто-то может долго и усидчиво ботать, невзирая на мирские соблазны, а я не очень, только если изолироваться как инок какой-нибудь
алсо чет современная физика таки похожа на маняматику
в первой яйцеголовые придумывают непротиворечивые манятеории, чтобы из них выводились и типа объяснялись результаты экспериментов и манятеории другого уровня
в маняматике, например, придумали те же манямножества, на их основе тоже пытаются вывести остальную маняматику. ток эксперименты тут только над числами и другими абстрактными объектами интереса маняматики. то есть маняматика делает зализон самой себе, а маняфизика - суровому ирл миру
где в моем манярассуждении даунича слабое место?
в первой яйцеголовые придумывают непротиворечивые манятеории, чтобы из них выводились и типа объяснялись результаты экспериментов и манятеории другого уровня
в маняматике, например, придумали те же манямножества, на их основе тоже пытаются вывести остальную маняматику. ток эксперименты тут только над числами и другими абстрактными объектами интереса маняматики. то есть маняматика делает зализон самой себе, а маняфизика - суровому ирл миру
где в моем манярассуждении даунича слабое место?
У меня еще есть ощущение, что вопрос тупой, а я не могу это понять. Если так, то по-другому вопрос задаю. Почему в серьезных книгах по терверу нет геометрической вероятности
Аноны, в свое время я практически не учился. В особенности это касается математики. Сложение и вычитание более-менее знаю и в повседневности этого хватает, но вот с умножением и делением все не так радужно (Хотя и не сказать что совсем дуб дубом). Теперь жалею что раньше не спохватился, но ведь не все потеряно, чай коньки отбрасывать не собираюсь.
Ближе к делу - подскажите хороших книг по математике с первого (Лучше перебдеть и прочесть с самых основ, даже если ничего нового не узнаю) и по десятый (Или какой нынче конечный) классы. Желательно - с ссылками на файлы или онлайн.
Если есть лучший, нежели учеба по школьным книгам, способ - с радостью выслушаю.
Ближе к делу - подскажите хороших книг по математике с первого (Лучше перебдеть и прочесть с самых основ, даже если ничего нового не узнаю) и по десятый (Или какой нынче конечный) классы. Желательно - с ссылками на файлы или онлайн.
Если есть лучший, нежели учеба по школьным книгам, способ - с радостью выслушаю.
>У вас за всё время разве что Наполеоном не был.
Да ладно, Мунина забанили 22 в 00:00, вечером этого же дня ты объявился. Совпало типа, ну да, ну да. Может и совпало, но всё равно подозрительно, учитывая и то, что о Мунине пишут деды
Двоичная система стара как мир. Давай придумаем свою.
А давай, чёрт с ним. Для начала нужно определиться нужен ли нам 0.
Хочу систему счисления, в которой 0 был бы равен бесконечности и это не вызывало бы противоречий. Но у меня такие рассуждения вызывают system failure.
Ну, и 0, и бесконечность штуки фиктивные. Хранятся лишь указания на оные, а самых оных нет.
Не, именно равно, одно и то же, приблизь ноль, точку, и получишь целое. Один объект. Да ты понял, о чём я
Забей, уже шифер прохудился опять, подтекать начинает.
>Один объект
Это и будет единица. Не, всё, system failure, ты меня реально уделал, пойду ка я спать.
Я полковник, слышишь, вставай. Мы с тобой пойдем на парад. Ты не бойся, братишка, нас давно там ждут.
>Это разные уровни уже.
А в том и прикол, что в нашей системе счисления не должно быть никаких уровней.
Трудно ли изучить математику в объеме первого курса математического факультета самостоятельно?
При определенных усилиях, естественно. Меня интересует именно трудность по сравнению с тем как если бы я учился на матфаке.
Элементарный вопрос дебича по элементарной матеше. Сократить показатели радикала и выражения под ним
Ответил к пикрилу - кубический корень из 3a^2b^4, но вдруг неправильно в учебнике чуть другой ответ
Ответил к пикрилу - кубический корень из 3a^2b^4, но вдруг неправильно в учебнике чуть другой ответ
32/6a4/6b8/6 =
31/3a2/3b4/3 =
∛(3a2b4)
Поэтому учебник прав.
А все из за того что в учебниках не пишут что степень это сокращенная запись умножения одинаковых чисел, а корень обратная по свойствам операция степени.
Там вообще дохуя чего не пишут, думают что это МОЖНО ЗАМЕТИТЬ ПОСЛЕ НЕБОЛЬШИХ ПРЕОБРАЗОВАНИЙ ЧТО ЭТО ОЧЕВИДНО ЧТО И ТРЕБОВАЛОСЬ ДОКАЗАТЬ. То же умножение не пишут как суммирование одинаковых чсел, чем и пользуются рыбниковы с РУСами.
Лжоти, все там пишут. Даже в арифметике никольского написано именно это
Почему в книгах по математике так мало картинок? Можно же порисовать хоть возле начала глав каких-то человечков, разве нет?
А числовая прямая и графики чем тебе не картинки? Можно самому по вкусу добавлять конных арбалетчиков и цветочки
Трудно ли засунуть хуй в пизду или наоборот? Так же и здесь. С одной стороны, ебля (соответственно, самообучение) – естественный процесс, с другой стороны, придётся встретиться с неестественными трудностями: от государства, которое не даёт проституции нормально распространиться и до общественных предубеждений, будто просто поебаться есть плохо.
Я верю, что обучиться математике до высшего уровня самостоятельно можно (потому что отчасти сам таков), но полностью самому не выйдет и сам путь чрезвычайно тернист.
Если есть возможность, надо идти в ВУЗ. Программа там будет говно, но главное это обсуждение и заинтересованные люди.
>или наоборот
Интересно. Наверное, очень трудно и почти невозможно.
Не, пикрил ответ в учебнике, поэтому я и переспросил
Часто бывает так, что правота учебника мне не очевидна по какой-либо причине, поэтому я перепроверяю себя лишний раз
Повторением арифметики. Например, как раскрывать скобки помнишь?
> в учебниках не пишут что степень это сокращенная запись умножения одинаковых чисел, а корень обратная по свойствам операция степени.
> умножение не пишут как суммирование одинаковых чсел
Что же там можно писать, если не это?
Какая подготовка нужна для курса лекций Ромчика с четвёртого пика?
Почему математика не может преподноситься как вирусные мемы?
Ох уж эти шизики.
Мне вот приятно находить неточности и опечатки в учебнике.
Как самостоятельная эволюционирующая форма жизни, существующая в "пространстве" человеческого сознания :)
Мне вот приятно находить неточности и опечатки в учебнике.
Как самостоятельная эволюционирующая форма жизни, существующая в "пространстве" человеческого сознания :)
Ах, ну если мем это по сути то же, что я описал. Давно уже читал мистера Докинза
Ну, там вирусные видео на ютубе, где школьники на серьезных щщах обсуждают какую-то математическую теорию, делают "версус" между разными теориями, кучу всякого подобного.
Каких мемов? Я про вещества. Закинулся и сразу всё понятно в лекциях Ромчика с четвёртого пика.
У вас тоже бомбит, когда интуитивно понятна справедливость несложного утверждения, но доказать его строго ума не хватает?
По каким тегам смотреть? Хочу разогреть свою жопу интеллектуальными успехами сытого поколения
На отсутствие чувства юмора? Или на тупые вопросы про мемы и малафью?
Книгами с настоящей современной элементарной математикой.
Например, Теория множеств + 4 тома Алгебры:
1) http://libgen.io/ads.php?md5=3ED34E22D532E5CD3B50264BB1DDA98F
2) http://libgen.io/ads.php?md5=62A1360ABC64261ADE138E988A50A7E1
3) http://libgen.io/ads.php?md5=158A9F41B657A57D70838E4CA9BE5E27
4) http://libgen.io/ads.php?md5=77214849E973649C7B5668EFC2C96F6D
5) http://libgen.io/ads.php?md5=07D765BF4A78B4134D661C97F0BFB16D
Или Aluffi http://libgen.io/ads.php?md5=4F96A779AF25BA43A7631FF8E7E6156B – только обязательно найди список ошибок. Или попробуй достать второе издание.
>52 года прошло
>современной
КоАП РФ, Статья 6.13. Пропаганда наркотических средств, психотропных веществ или их прекурсоров, растений, содержащих наркотические средства или психотропные вещества либо их прекурсоры, и их частей, содержащих наркотические средства или психотропные вещества либо их прекурсоры, новых потенциально опасных психоактивных веществ
>На отсутствие чувства юмора?
В каком месте ты тут пропаганду увидел, шизик?
Так такого вроде пока нет.
А что круче ZFC или NBG?
Очень, оченьь бомбит, но учитывая какие легчайшие штуки я не могу придумать как доказать, лучше мне помолчать
Помогите, тянка поставила условие отношений - привести краткое доказательство Великой Теоремы Ферма, что делать?
Однохуйственно по теореме Мостовского.
Выведи из ABC-гипотезы, затролль тянку.
А если она его за это ножом в брюхо пырнет?
Выведи из ТНН-гипотезы
Я кое-как в итоге "доказал", но нет поблизости математика, который оценил бы мои писульки и указал на слабые места.
Казалось бы, нахуя вам даден двач?
А за что? Так-то доказательство действительно короткое. А дальше все вопросы к Мочидзуке.
Почему тогда рыбниковы пишут что 2*1=2 а 1х2=1?
Давай разберем по существу, шлюхорен, почему нужно изучать теорию множеств заместо наглядных примеров?
Ананас, а используешь ли ты анки, чтобы учить и запоминать математику или другую естественную науку. Столкнулся просто с проблемой как составлять карточки.
Например, после глав часто идут вопросы, исключая примерчики всякие. Например, что такое кратное? что такое множество? Стоит ли их заносить в карточки, вот в чем вопрос.
Или вот например какоениудь доказательство, что a + b = b + a. С одной стороны надо, а с другой просто боюсь выполнить лишнюю работу, запоминая не то что нужно.
Почему не спрашивают в анки треде? ПОтому что ленив, и врядли найду там математика, там в основном языки учат
Например, после глав часто идут вопросы, исключая примерчики всякие. Например, что такое кратное? что такое множество? Стоит ли их заносить в карточки, вот в чем вопрос.
Или вот например какоениудь доказательство, что a + b = b + a. С одной стороны надо, а с другой просто боюсь выполнить лишнюю работу, запоминая не то что нужно.
Почему не спрашивают в анки треде? ПОтому что ленив, и врядли найду там математика, там в основном языки учат
Тут вариантов не много, либо он делает это специально, либо не специально. Если первое, то он мошенник и сука, если второе то сумасшедший и неуч. Выбирай любое
Киньте пасту про то как с помощью теории множеств доказывается существование ктулху.
У него и спроси. А сам быстро привёл пример учебника, где бы об этом не говорилось.
Стыдно. Вот само задание.
Докажите обобщение законов де Моргана для любого конечного набора множеств:
A1∩A2∩A3∩…∩An = A1∪A2∪A3∪…∪An
A1∪A2∪A3∪…∪An = A1∩A2∩A3∩…∩An
ща облажаюсь с разметкой
Что за анки? Если это очередное тульпоёбство то не нужно. Когда приходит понимание чего-то, приходит и запоминание. От этого и отталкивайся.
Если двум дать одну яблоко, то получат яблоко двое. Если одному дать два яблока, то получит лишь один.
Просто система для spaced repetition, для более лудтшего запоминания
Ну так они дают только примерный результат, а мне нужно точно как в аптеке.
Да, устремить к бесконечности можно, но готовых формул почему площадь под кривой равна куб делить на три они не дают. Можно ЗАМЕТИТЬ что таки да, предел суммы стремится к этому значению, но вывести правило не получится.
Хз, у меня, например, плохая память, не уверен, что память нужна для математики, хотя, конечно, с хорошей памятью гораздо проще вот это вот всё. Буквально вчера где-то видел цитату Пуанкаре по этому поводу, ща поищу.
Как быстро от знаний 6 класса перейти где-то к преобразованию Фурье? Может есть шаманство какое-то?
Какая-то хуита. Лучше примеры решай, а не трать время на подобное.
Все в голове не удержишь же.
В этом видна польза абстрагирования и доказательств, один раз докажи - эн раз пользуйся, без необходимости каждый раз разбирать на анальные составляющие и держать их все в уме
Ну почему же, теоремы. Аксиома это все тян шлюхи.
Всt тян шлюхи, шлюхи не нужны-> тян не нужны
Все тян шлюхи, шлюхи должны получать по еблу->ББПЕ
Я даже не знаю что такое строго упорядоченное множество, как я могу задать определения?
Школота какая-то набежала. Оставлю свое горе-доказательство на потом.
Что-то не могу осилить Куранта. Какие-то инверсии, самолетики бумажные строит... Как это понять?
Не знаю, ты первый начал.
Ты про теорему Ферма? Твоя тянка тебя тральнула, там док-во на 50 страниц, а другое ты вряд ли придумаешь.
Читать пока не поймешь. Читать то хоть %%само??обучен вдумчиво?
Ты даже с самолетиками понять не можешь?
Читай тогда смирнова или илью-поздняка
>Читать пока не поймешь.
Соглашусь с предыдущим оратором. Если и после этого не поймёшь гугл к твоим услугам, возможно именно этот момент Курант плохо объяснил или просто ты туповат, но что поделать. Главное не пропускай непонятное. Ещё попробуй сделать паузу на пару дней, может ты просто перенапрягся и мозг бунтует, отказывается новую инфу воспринимать.
Я просто тут (170 страница) только самолетик и вижу. Так скучно всё как-то. Не понимаю зачем это нужно. С третьей главы "Геометрические построения. Алгебра числовых полей." я совсем ничего не понимаю.
> С третьей главы "Геометрические построения. Алгебра числовых полей."
Возвращайся. Нахуй ты пропустил? Возвращайся, иначе дальше читать смысла нет вообще. Я так тоже типа книжки читал раньше, вот только в одно ухо влетело, в другое вылетело, потом только это понял.
А если взять чуть конкретней по теме? Вот понятие поля я чуть сам не придумал с первых двух глав. Далее он делает какие-то геометрические построения дабы показать почему именно 4 операции - плюс, умножить, минус, делить есть такими, что-ли основными, и типа для них нам достаточно геометрически выполнить лишь построение линий, а для корня уже надо, например, циркуля дабы сделать полукруг. Это единственное, что я понял. Да и то интуитивно.
Ну, и в той главе до которой я дошел пропуская он говорил вроде о чем-то вроде поворотов плоскости, фигур... У меня ассоциации с символами, точнее с их обозначениями. Например, можно сделать символ абстрактного бублика и его можно всячески поворачивать так-то и так-то, а другое обозначение уже меньшими способами можно поворачивать. Но это какой-то дошкольный уровень у меня.
Теряешь лес за деревьями.
И что делать с этим?
Ну что делать, если и правда теряешь общую картину, то надо работать дальше, стараясь помнить о такой своей ошибке. Хз что тут кроме общих слов посоветовать
Попробуй сделать паузу, мб ты просто перенапрягся, пусть в голове всё утрясётся, походи по улице и всё такое.
И там отсылки к "элементарной геометрии".
Придется прочитать учебник, прежде чем лезть в такую заваруху.
Киткатом предлагаешь упороться?
Проблемы с этой хуйней.
Начал составлять дерево возможностей без учета почти правильного предугадывания второго знатока.
Начал делать как на 2-ом пике, но потом просчитал сколько вариантов и охуел.
То есть, после А не может быть В, после В - С и т.д. +в цепи не могут повторяться номера.
В первом ряду не может быть А, во втором В, в третьем С и т.д.
Уже хз как решить.
Начал составлять дерево возможностей без учета почти правильного предугадывания второго знатока.
Начал делать как на 2-ом пике, но потом просчитал сколько вариантов и охуел.
То есть, после А не может быть В, после В - С и т.д. +в цепи не могут повторяться номера.
В первом ряду не может быть А, во втором В, в третьем С и т.д.
Уже хз как решить.
Два угаданных места находятся в одной паре и стоят на своих местах, вторая пара должна стоять не на своем месте.
Если он угадал DA, то есть два варианта расположения: (DA)B(EC) или (DA)(CB)E, оба не подходят. Угадать пары AE и EC нельзя т.к. вторую пару некуда переставлять. Угадана пара CB, тогда:
E(DA)(CB) или (AE)D(CB). Второе не подходит.
Ответ: EDACB
черт, как же всё просто оказывается.
Спасибо!
Бамп.
И чего здесь сложного?
Если х лежит слева, тогда х не лежит в пересечении Ai, тогда x не лежит в каждом Ai[/sup]. Если х лежит справа, тогда он содержится в каком-то дополнении Ak, из этого выходит, что х не принадлежит Ak, следовательно х не лежит в каждом Ai.
Блядь, лучше кнопку юзать
Если х лежит слева, тогда х не лежит в пересечении Ai, тогда х не лежит в каждом Ai.
Если х лежит справа, тогда он содержится в каком-то дополнении к Ak, из этого выходит, что х не принадлежит Ak, следовательно х не лежит в каждом Ai.
Котятки, можете подсказать, с чего начать решение?
с вольфрама
Вольфрам больно хитрые замены предлагает, здесь, чую, должен быть какой-то простой и очевидный, для неглупых людей, путь.
Если ты хочешь быть математиком, что такие упражнения довольно быстро атрофируют любые математические способности, необходимые для современной математики.
Ты за то, чтобы перенести все тривиальные вычисления на компьютер?
Работа с интегрирование и дифференцированиеи суть работа со сложением натуральных чисел на калькуляторе. Бесполезное.
Занимайся современной математикой в сторону Фано или изучай Maple, если интегралы тебе для физики или химии.
Универсальная тригонометрическая подстановка и ниибет.
Ничего. Меня волнует лишь строгость.
Я предполагаю, что либо мощность множества множеств, входящих в пример к данному закону |Α| = 2, и тогда справедливость очевидна, либо |Α| = 2m, и тогда можно разбить их все попарно, применить закон, потом применить к результатирующим множествам из данных парам и т.д. получить в итоге правую часть равенства благодаря свойству транзитивности любой из операций ∩ ∪. В случае с |Α| = 2m + 1 все точно то же, только конечное множество после обработки всех четных пар ставится в пару с оставшимся, который выше сопоставлен с 1 и снова все збс
Правда, я не могу сформулировать это на строгом языке, и мой перфекционизм начинает зудеть. Или я вообще довен и написал хуйню
бэмп
Я, честно, нихуя не понял.
>благодаря свойству транзитивности любой из операций ∩ ∪
Теперь объясни, как операции могут быть транзитивными?
Поле Галуа это как обычное поле, но там конечное множество чисел?
Я попутал. Они ассоциативны. Спасибо за уточнение.
Какой физический смысл у эволюты? Нахуя её придумали?
Лол, кое кого пидорнули.
А в чём суть? Транзитивность про бинарные отношения, а ассоциативность про тернарные? я школоло, не бейте, лучше обоссыте
Суть в том, что это разные вещи.
бинарная операция на X - это функция на X2 со значениями в X. Бинарное отношение на X - это подмножество X2
A binary operation f on a set S may be viewed as a ternary relation on S, that is, the set of triples (a, b, f(a,b)) in S × S × S for all a and b in S.
А это враньё или интерпретация просто?
Верно всё. f(a,b) → c можно записать как тройку (a, b, c).
>for all a and b in S
Так же у тебя для любой пары (a, b) определенно(на всем S2 задана функция), тогда как отношение - это подмножество S2
Ок, спасибо, я всё понял.
Непонятно написал после зеленой строчки. Хотел другое сказать, ну похуй. Вообще простыми словами - если на S задана операция, то это значит, что если ты возьмешь любые 2 элемента, то с ними будет связан 3-тий элемент(результат операции? не знаю, есть ли для этого спец. название). Если на S задано отношение, то ты, возможно, вытянув 1 элемент вытянешь и привязанный к нему(причем порядок важен, вытянув х ты можешь потянуть за ним y, но потянув за y ты можешь и не вытянуть х).
>Непонятно написал после зеленой строчки.
Полностью понятно, разжёвывать необязательно было теперь я только запутался сильнее, но всё равно спасибо.
В общем если бинарное отношение это подмножество декартова произведения S на S, то бинарная операция это отображение, ставящее в соответствие каждой паре из SxS единственный элемент в S?
>Так же у тебя для любой пары (a, b) определенно(на всем S2 задана функция), тогда как отношение - это подмножество S2
В общем вот так понятно и ладно. Ещё раз спасибо.
Короче, блин, там два, тут три, там бинарное, тут тернарное, там транзитивность, тут ассоциативность, там площадь, тут объём. Разные вещи.
Ты сам меня сейчас запутал.
Мне непонятно, как на S3 вводить ту же транзитивность?
Если принимать за бинарную операцию - подмножество S3, то да, бинарная операция будет сорт-оф 3-рное отношение, только с 2-умя условиями. Причем в твёом определении написано только 1. Если напишешь, как на n-рном отношении определить транзитивность, то да, операции могут быть транзитивными.
>как на S3 вводить ту же транзитивность?
Так никак же, это свойство бинарных отношений. А тут S3. Или я тебя не понял?
Ну типа например есть у нас 3+3=9
Есть пара (3,3), есть отношение эквивалентности(бинарное), есть бинарная операция +, и вот у нас получается уже тернарное отношение (3,3,f(3,3)=9). Я вот так понял. Это верно?
>тернарное отношение (3,3,f(3,3)=9)
Ой,ну то есть тройка получается, а не отношение. Отношение как раз плюс. Отношение, ставящее в соответствие каждой паре (a,b) из SxS единственный элемент f(a,b) из S. Транзитивностью оно обладать не может вообще, так как не бинарное, а тернарное, а транзитивность свойство бинарных отношений. Зато обладает ассоциативностью, свойством тернарных отношений. Верно?
>ну то есть тройка получается, а не отношение.
Хотя это тоже отношение. Или нет? Тернарное отношение это любое подмножество множества SxSxS, функция или отображение это отношение, удовлетворяющее условию, чтобы "каждому соответствовал единственный", то есть это все такие тройки. Всё, я окончательно запутался. Жду твоего ответа.
Отношение. Бинарная операция тогда - тернарное отношение, удовл. 2-ум условиям
1) если есть тройка (a, b, f(ab)), то она единственна для данных a, b
2) каждый a, b входит в какую-то тройку.
Т.к. на тернарном отношении нельзя задать транзитивность, а только на бинарном, поэтому операция этим свойством обладать не может.
Ок, всё понятно.
Как же одна моча меня боится. Просто трясётся!
Бамп, ну.
Посоны, поясните за гиперболический параболоид. Это ведь по сути одна парабола насаженная на другую.
Вот уравнение: x^2 - y^2 = z
Занулим x = будет парабола. Занулим y - будет тоже парабола, но с ветками в другую сторону. При z = 0 там прямые.
Внимание, вопрос: почему он тогда так называется - гиперболический? Где там гиперболу увидели?
Вот уравнение: x^2 - y^2 = z
Занулим x = будет парабола. Занулим y - будет тоже парабола, но с ветками в другую сторону. При z = 0 там прямые.
Внимание, вопрос: почему он тогда так называется - гиперболический? Где там гиперболу увидели?
Хотя нет, смотри: тройку (a, b, f(ab)) можно записать как пару ((a, b), f(ab)). Но такие пары не обладают транзитивностью, т.к. нет ни одной пары, где на первом месте было бы f(ab).
Ты специально запутываешь анончика?
Бинарное отношение - это ведь по сути тоже функция (назовем ее R). Только X2 отображается не как обычно на X, а на множество из двух элементов, например, {0; 1}. Или {false, true}, не важно. Т.е. функция эта дает нам знать, находятся два элемента в отношении или нет.
Пусть тебя не смущает, что в определении транзитивности фигурируют три элемента. Связываются-то они все равно парами, т.к. отношение бинарное.
Если a отношается с b (т.е. R(a,b) -> 1)
и b отношается с c (т.е. R(b,c) -> 1)
то a отношается с c (т.е. R(a,c) -> 1)
Везде бинарные отношения, никаких тернарных нет.
Так транзитивностью бинарные отношения могут обладать, а могут не обладать, но тернарные уж точно обладать не могут, это свойство онли бинарных.
>Ты специально запутываешь анончика?
Анончик, без обид, но вот как раз ты и запутываешь. Бинарное отношение это подмножество S2, тернарное это подмножество S3, отношение это не функция же, наоборот верно, а туда неверно, мб ты с отображением спутал? Но бинарная операция, которая по сути тернарное отношение, функция, ыыы.
>Везде бинарные отношения, никаких тернарных нет.
Ну нет же, отношение это подмножество некое AxB, если A=B, то оно называется бинарным, по аналогии если S3, то тернарным. Там тройки, тут двойки, и свойства разные, транзитивность свойство только бинарных отношений. Ну правильно же по идее, или нет?
> это свойство онли бинарных.
Ну типа транзитивность тернарных или ассоциативность бинарных это как площадь куба или объём квадрата. Смысла не имеет. Ну это я так понимаю. Может неправильно.
> ((a, b), f(ab))
>Связываются-то они все равно парами
Так нет, например 3+3=6, для +, который ассоциативная, коммутативная, дистрибутивная бинарная операция, тернарное отношение это (3,3,6), для =, которое отношение эквивалентности, которое транзитивное, рефлексивное, симметричное это ((3,3), 6).
Нарисуй график в трехмерном пространстве и увидишь.
В первом контейнере находится 3 коробок с посудой и 6 коробок с книгами, а во втором контейнере находится 5 коробок с посудой и 5 коробок с книгами. Из каждого контейнера наугад выбрали по две коробки. Чему равна вероятность того, что из выбранных четырех коробок ровно две с посудой?
В ответе 13/72, у меня получилось 7/18. ЧЯДНТ?
В ответе 13/72, у меня получилось 7/18. ЧЯДНТ?
У меня есть система. Я вычел из первого уравнения второе, получил диофантово уравнения, нашёл серию корней. Но при подстановке обратно в систему они чаще всего не подходят. ЧЯДНТ?
Ты не избавился от второго уравнения, поэтому нужно искать значния, которые являются и его корнями.
Ананасий, а в алгебре Шеня дается шишре или глыбже материал, чем в учебниках школьных? Могу ли я заменить учебник этой книгою?
Шень крутой мужик, но книг его не читал.
На мой взгляд не нужно делать этому дурачку лишний пиар, забвение лучший метод борьбы с такими персонажами.
Можешь, но там не все темы из школьного курса. Основное отличие от учебников, что задачки требует гораздо большей смекалочки. Одного здешнего анона они довели до слёз, например.
В таком случае, ожидайте второго плаксу, потому как... впрочем, похуй
>Одного здешнего анона они довели до слёз, например.
А на какой задаче? Есть ссылка на тред? Давно не плакал.
Двачую. С Вхореном так же нужно поступать.
Не только занули z, а положи z=const. Горизонтальные слои там гиперболы.
Я закончил читать и усваивать математику по курсу диференциалы и интригалы.
Куда двигаться дальше? Что читать?
Куда двигаться дальше? Что читать?
Рили.
Спасибо, анон.
И как я сам не допер?
Анализ на многообразиях.
Книжку давай.
Спивак Анализ на многообразиях.
Посоветуйте хорошую книгу по комбинаторике.
Виленкин Комбинаторика.
Анон, решил кроме повторения математики еще парралельно читать книгу по логике. С вопросами по логике в сцы или можно сюда?
Можно сюда
Толстяк.
Так вот. Совершенно хз что читать, скачал несколько книг, и все совершенно разные, запутался только.
Например, скачал Арно И Николь "Логика, или искусство мыслить, где помимо обычных правил содержаться некоторые новые соображения, полезные для развития способности суждения."
Думаю, вполне очевидно, что книга старовата.
Приведу цитатку из "Рассуждения первого", это что-то навроде введения.
Разумом пользуются как инструментом приобретения познаний, а следовало бы, наоборот, познания использовать как инструмент совершенствования разума: ведь правильность ума несоизмеримо важнее любых умозрительных знаний... Поэтому благоразумные люди должны предаваться научным занятиям лишь постольку, поскольку они могут служить названной цели...
Думаю, понятно, каким языком написана книга.
Дальше идет Бочаров Маркин Введение в логику, Это обычный такой учебник ВУЗовский,, рекомендованный для гуманитариев, в основном как я понял это учебник ля филфака МГУ.
Третья книга, которую я проглядел была "Современная логика. Теория и практика" Шумана. Довольно интересная, но и для понимания я нашел ее трудной, тк используются какие-то философские словечки.
Приведу цитату из предисловия
Традиционное деление курса логики отражает исключительно аристотелевское понимание принципов ее построеня...
Оно просуществовало на Западе вплоть до конца 19в. Наиболее популярный такой труд - Арно и Николь[1662]. Однако в современной логике такие категории как "понятие", "суждение" и "умозаключение" были признаны в высшей степени проблематичными..."
Вобщем курс этой книги нетрадиционный, и в книге обсуждаются три раздела логики матлогикка, вероятностная и неформальная.
Поразила еще глава по краткой истории логики, а особенно упражнения к нему, вот зацените
На основании библейских текстов самостоятельно воспроизведите моделирование рассуждения Ханаан, хананеи.
Надо сказаь, учебник интересный, но явно для феласафоф, потому как первоеж понятие "ниверсум" тут же не поясняется.
Короче, я накачал какихто хардкорный трудов, и не знаю с чего начать
Это я еще не упомянул "Искусство спора" Поварнина, который в этой книге надеется обучить быдло спорить разумно, хотябы зная значения слов "социализация земли", или "буржуазия". Книги Поварнина вобщем то научно популярны
С такой логикой в /b
Вроде сколько чисел в десятичной записи числа 2100.
В чём подвох?
Бамп.
Одно, 2^100
Не в форме степени
Чисел или цифр?
Цифр да
Гайс, очень хелп плз.
Как вы знаете есть задачки коммивояжёра:
Имеем 20 точек и пути между ними четное кол-во путей из каждой вершины.
Начав из точки А в нее же и вернемся, пройдя все 19 чекпойнтов самым выгодным маршрутом.
Моя задачка: есть 40 точек и пути между ними.
Начинаем в А, требуется пройти любых 29 чекпойнтов самым выгодным маршрутом. 10 вершин должно остаться без внимания.
Куда читать? Где могут быть такие примеры?
диплом строится на этом, если есть фланеры-энтузиасты могу расписать подробнее, но вряд ли оно надо
Как вы знаете есть задачки коммивояжёра:
Имеем 20 точек и пути между ними четное кол-во путей из каждой вершины.
Начав из точки А в нее же и вернемся, пройдя все 19 чекпойнтов самым выгодным маршрутом.
Моя задачка: есть 40 точек и пути между ними.
Начинаем в А, требуется пройти любых 29 чекпойнтов самым выгодным маршрутом. 10 вершин должно остаться без внимания.
Куда читать? Где могут быть такие примеры?
диплом строится на этом, если есть фланеры-энтузиасты могу расписать подробнее, но вряд ли оно надо
Что толстого? Нормальная книга же.
Дорогой анон! Посоветуй, пожалуйста, книгу по статистике, чтобы совсем для глупых, все понятно было. Спасибо.
Я б тебя понял, если б я сюда марксистскую диалектику притащил
Это разве решамемо?
NP полнота там. Эвристически может и да, но это вряд ли по адресу.
>NP полнота там
я аут-менджер, пожалуйста не кидайтесь такими умными словами, даже прогуглив я не вдуплил
Повторюсь: у меня всего лишь есть матрица 40х40 условно точка старта и например 29 "ходов", что бы оптимально вернуться (не наступая дважды)
звучит очень просто, как мне показалось
>не вдуплил
Нет алгоритма, который решил бы задачу за разумное время.
>аут-менеджер
Страшно спросить.
Что значит самым выгодным маршрутом?
У тебя и так уже социализация земли с буржуазией полезла.
Ну смотри, NP-полная задача простым языком это такая задача, решение которой проверить легко, но найти это решение охуеть как трудно. Например, найти гамильтоновкоторы бы проходил только один раз по всем вершинам путь в графе, проверишь легко, а найти совсем нет. Твоя задача в общем случае, задача коммивояжера, как раз переформулировка этой задачи, то есть для неё есть экспоненциальный алгоритм, который даже на 400 вершинах будет работать дольше, чем горит Солнце. С точки зрения математики больше мы тут ничего сделать не можем. Но тем не менее навигаторы исправно работают, карты гугла прокладывают маршруты и тд С точки зрения инженерного дела, в частности Computer Science мы сделать можем что, есть алгоритмы, которые называются эвристические алгоритмы, для них нихуя не доказано, но они работают, и работают они далеко не всегда, могут быстро работать, могут вечность, всё в таком духе. Потому тебе не на эту доску, а в pr или sci. Как-то так.
>я накачал какихто хардкорный трудов
По философии какой-то. Бери Шень Логика. И доказывай там всё, главное, не пропускай упражнений, затем читай правила демагога и будешь овнить любой тред в /b, на завтрак анончиков кушать, точнее перед завтраком, хорошая разминка, кстати, в Древней Греции регулярно такие тренировки проводились.
Проводились, потому как, если верить третьему означенному мной труду, от риторики логики и убедительности оче зависело их положение. Смог Ерохиуса прилюдно раскатать - честь и хвала, не смог - вае виктус. Короч, как бы то нибыло, согласно книге формальная логика НИНУЖНА, сегодня как основа математическая первого порядка, + rational thinking and scientific method а на этом уже строятся вероятностная и неформальная.
За Шеня спасибо, с него и начну.
ps Неужели это все один и тот же Шень, или там даинсатия
>, согласно книге формальная логика НИНУЖНА
Согласно хуиге, я тебе в другой ситуации тоже с три короба в уши насру и ты поведёшься. Если хочешь уметь убеждать ты должен уметь мыслить для начала, иначе рискуешь превратиться из демагога в долбоёбв. В этом тебе поможет Логикая считаю, что логика может быть только одна, логика от слово Логос, кстати. Всё остальное философия ебаная, ты сам таких книжек сможешь с десяток настрочить. Ну а дальше гугли правила демагога и пользуйся. Равных тебе не будет если не пересечёмся, но я только за, от качественного противника получаю огромное удовольствие.
Один и тот же Шень. Я же говорю, Шень крутой мужик, но Катющика всё же зря пиарит.
Где он его пиарит?
>На мой взгляд не нужно делать этому дурачку лишний пиар, забвение лучший метод борьбы с такими персонажами.
Ну в плане
зря он вообще о нём упоминает.
>в Древней Греции регулярно такие тренировки проводились
В /Ь/?
Там больше всего народу, выбираешь сноба-умника пожирнее да почванливее и начинаешь представление, публика аплодирует, почему нет? Суть же не противника убедить как бы, а толпу. На дваче все анонимны, потому давления авторитетом нет, идеальная площадка для тренировки ораторского искусства.
Это не Шень вообще, Шень полукитаец.
>аплодирует
Две п , кнопка залипла.
молниеносный фикс
Да Шень же.
>Да Шень же.
Кек, это не Шень, зрение хуёвое.
На пике Шень, на видео Бояршинов, зачем троллишь бля.
В смысле проблемы с распознаванием лиц короче. Отстань, я поехавший, ааааа.
Ну ты спрашивал про Шеня, потом скинул видео, я видео открыл, там мужик по форме напоминающий Шеня что-то загонял, я распознал его как Шеня. Это сложно в общем. Не бери в голову.
>по форме напоминающий Шеня
Так. Тоесть, как бы наверное сказал тополог, гомеоморфный Шеню.
Лол.
Не, не интересно. Катющик хотя бы смешной.
https://www.youtube.com/watch?v=mtum1K1dlfU
Я уссыкался вместе с ним с этой херни, 20:54
https://youtu.be/A2M60TiJvG8?t=1254
пока он про структурированную воду не загонял даже была мысль, что он адекватен, просто чувство юмора такое, тролль типа. А оказалось, что он сам дурачок, так ещё и питается тем, что подобные ему высирают
Рыбников тоже смешной, слышь
Ну хз, у меня истерика была с селёдочно-карандашного континуума, а Рыбников просто шизик скучный какой-то.
Вы так говорите не обращать внимания, как будто это что-то хорошее. А по моему с невежеством нужно бороться.
Ты о чём?
Если о нём говорить, то люди будут думать, что в этом что-то есть и создаётся лишний пиар.
А если о нем не говорить, то оно будет без труда самопиариться и распространяться. Впрочем, это не про математику, не хочу уж тут споры разводить
>без труда самопиариться
Так не бывает. Впрочем, да, это не по теме.
аут=аутист
>>Нет алгоритма, который решил бы задачу за разумное время.
а если заменить 40 на 5, а 29 на 4, то будет всего 625 вариантов, такое уже должно моментально считаться, нет?
вроде бы уяснил, спасибо, пойду туды
>выгод
кротчайшим
бля, кратчайшим*
Бля, ну...
Я осилил вводные курсы высшей математики и могу интегрировать и дифференцировать под сабатон.
Что читать дальше, чтобы смог пойти в физику и инженеры?
Я осилил вводные курсы высшей математики и могу интегрировать и дифференцировать под сабатон.
Что читать дальше, чтобы смог пойти в физику и инженеры?
Картофан какой-нибудь
кратные интегралы, ряды, ряды Фурье, дифференциальные уравнения (обыкновенные и в частных производных), теория поля гомологическая алгебра
Помогите, а то я что-то торможу почему-то, за пару минут не могу додуматься (я правда и стереометрию не очень и знал, но да ладно). Задачка на функции для девятого класса.
Зависит ли объем куба от площади его поверхности? Если ответ положительный, то какой вид имеет эта зависимость?
И помогите понять как находить подобные зависимости.
Зависит ли объем куба от площади его поверхности? Если ответ положительный, то какой вид имеет эта зависимость?
И помогите понять как находить подобные зависимости.
вырази сторону куба из площади и подставь в объем
Здесь стереометрия ни при чем.
У куба, по сути, только один параметр - это длина ребра. Обзовем ее а. А дальше очень просто.
Объем: a3
Площадь куба: 6a2
Нам нужно найти зависимость (т.е. вывести функцию) f(x), где x - площадь, а f(x) - объем.
a3 = f(6a2)
Теперь вопрос: что нужно сделать с 6a2 чтобы получить a3? Сначала разделить на 6, затем из полученного извлечь корень, затем полученное возвести в куб. Значит, зависимость имеет вид пикрелейтед. Подставь в пикрелейтед-формулу площадь и получишь значение объема. В нашем случае и объем, и площадь, выражены через a, но это не играет роли, можно подставить и конкретные числовые значения.
Как-то так, я думаю.
Спасибо. Изящно выходит.
Раздели на x^3.
А книжки про это все, книжки то
Ноль.
Желаю чтобы ты участвовал в постройке ядерного реактора, объебался с расчетом его параметров и был винвен в смерти более десяти миллионов людей. А все из за твоей тупости, не знающей границ и как находить пределы на бесконечности.
Прелесть технических профессий в том, что долбоеб, который плохо учился, просто не сможет работать по специальности, даже если получит корку.
Алсо, я не понял, зачем ты хочешь, чтобы он был виновен в эестерминатусе миллионов людей. Муки совести ему явно не грозят, т.к. совесть - это продукт высшей нервной деятельности и следствие развитости коры лобных долей. К тому же среди миллионов экстерминированных почти наверняка найдутся люди ни в чем не повинные.
По блату пройдет, он же гамолаг таполаг, может решить ящик в уме, вот и документы!
Потому что меня разбудили в семь утра чтобы сказать что я мясо неправильно заморозил, нужно было его кулечками отделить слой от слоя, а я не отделил.
Но ты и правда неправильно заморозил: теперь придётся всё размораживать ради одного кусочка, а потом опять замораживать.
>2k17
>замороженное мясо
А как ты предлагаешь мясо хранить? Или каждый день в магазин ходить?
То пор, значение знаешь?
Ну такое, пакет отдирать, рубить, потом мыть доску с топориком, проще по пакетам раскидать. Ладно, оффтоп какой-то.
Как понять, что передо мною не график функции, а что-то другое?
Несколько значений у соответствуют одному значению х.
То есть график функции не может проходить через ось y-ков (ординат или как там) более одного раза? А этого признака достаточно или есть еще какие-то?
Как посчитать количество монотонных булевых функций от трех переменных? Знаю, что это проблема Дедекинда, знаю, что не существует единой формулы, но препод требует объяснить простыми словами и показать все возможные монотонные наборы типа (00000000) и (00000001).
Перерыл весь интернет, нигде нет списка для трех переменных, только для двух (а там шесть наборов)
Перерыл весь интернет, нигде нет списка для трех переменных, только для двух (а там шесть наборов)
Без дополнительного условия почти самодвойственности, количество монотонных функций трёх переменных равно 20.
http://math.hashcode.ru/questions/85974/математика-число-монотонных-самодвойственных-булевых-функций-от-4х-переменных
График функции y = sqrt(x) - не график функции?
f(4) = 2, -2;
Перечитай мой пост, подумай.
Тоже перечитай и подумай. Этого достаточно. Насчет еще каких-то - да вроде нет.
Так ты сам ответь, y = sqrt(x) функция или нет?
По иксу не должны накладываться. Да. А круг нет. По иксу накладываются.
Это не функция. Если тебя это возмущает, то прочитай определение функции.
sqrt(x) ищет арифметический корень, который может быть только положительным.
Чё блядь? Так функция, или нет?
Да.Накладываться не должны, смотришь на X, там везде должна быть только одна точка.
Ясно, иди на хуй, знаток.
Вот тут по y накладываются, но всем похуй, это функция. Если ты её перевернёшь, то всё, уже не функция.
Ты сам то понимаешь картинку?
>Несколько значений у соответствуют одному значению х.
y=x, функция, а по твоему выходит. что нет
Очевидно, что да. Твоя картинка это доказывает в полном соответствии с моим определением. Кстати, перечитай его и подумай. Пожалуйста.
Нет, не выходит.
>Несколько значений у соответствуют одному значению х.
Выходит.
Куда смотреть?
В y=x одно значение y соответствует одному значению x, а у тебя несколько.
>Несколько значений у соответствуют одному значению х.
И другой пример. Тут несколько значений y соответствует одному значению x, но это не функция.
Да. Объясню на примере y = sqr(x).
Берем 2 листа. На 1-ом задаем функцию f1(x), таким образом: выбираем для y = sqr(x1) 1 значение, а другие определяем по непрерывности. Таким же образом задаем фнкцию f2(x) на втором листе. В точке 0 f1=f2, поэтому склеиваем листы в этой точке. Склеиваем так же по интервалу (0, -беск.) оба листа. Получится поверхность, на которой y = sqr(x) однозначна.
sqr(4) = 2, -2;
Это функция вида f:C->C или я ошибаюсь?
Это риманова поверхность функции заданной на комплексной плоскости.
Подумай еще. Еще раз перечитай .
Верно. Еще раз перечитай мой пост и подумай. Поспешишь - людей насмешишь.
sqrt(4) = 2. Пожалуйста, прочитай, например, статью на Википедии о квадратном корне - там подробно объяснен этот момент, с которым у тебя трудности.
Подумал, перечитал, действительно, я тебя не понял, как человек, прочитавший твой пост могу сказать, что такая формулировка сильно запутывает.
И не только меня, судя по ответам.
Квадратный корень из 4 = 2 и -2, потому что (-2)2 = 2 2 = 4. Чё за дичь ты городишь, нахуй мне твоя википедия.
А щито это такое?
мимо
Названия мне будет гаусс нашептывать?
Функция sqrt дает только положительный корень, долбоебушка.
sqrt = SQuareRooT.
>In mathematics, a square root of a number a is a number y such that y2=a
Дай угадаю, ты ебаный прогер или олимпиадник?
>The principal square root function f(x) = √x (usually just referred to as the "square root function") is a function that maps the set of nonnegative real numbers onto itself. In geometrical terms, the square root function maps the area of a square to its side length.
>is a function that maps the set of nonnegative real numbers onto itself
>nonnegative
Ясно, к нам господин из 17века пожаловал. Не вижу смысла дальше что-то писать.
Тоньше, пожалуйста, монитор от жира протирать пришлось.
Вопрос немного не в тему, но...
Почему элементарный учебник физики под ред. Ландсберга такой унылый, полный воды, скучный? За что его хвалят? Есть ли более насыщенные фактами книжки, а не эта дрисня для детсадовцев?
Почему элементарный учебник физики под ред. Ландсберга такой унылый, полный воды, скучный? За что его хвалят? Есть ли более насыщенные фактами книжки, а не эта дрисня для детсадовцев?
Поддержу, сразу видно совок писал
Потому что он
>элементарный
Читай лучше сразу курс общей физики
ФЛФ/Беркли/Сивухин
я уже видел этот ответ, но непонятно, почему перебор верных для двух переменных решений также верен и для трех переменных. Где обоснование, почему так можно? Или как мне в двух словах объяснить, почему я вдруг решил так перебрать эти решения?
А чего ты ожидал?
Бочку вина и озорных блудниц.
Надо было родиться аниме, извини
Ладно, тут такое дело, что курс школьной физики влетел мне в одно ухо и вылетел в другое, а заново повторять эту скучную муть я не хочу, оно ассоциируется у меня со скучными задачками и прочей школьной безнадегой.
В фейнмановских лекциях немного завис, когда там появился мат.аппарат, который я, по глупости своей, еще не знаю.
Корни из отрицательных научились извлекать в 18веке, благодаря Муавру и Котсу. Первым обобщил понятие функции до многозначной функции Галуа в начале 19века.
Как же скучно повторять арифметику. Вот уже поймал себя второй раз на том, что пропускаю сперва пару упражнений, потом всю тему, потом и целую главу, говоря себе "Я это поомню".
Арифметика - царица математики))
А кто тогда король
Ядро современной математики—это прежде всего анализ в широком смысле слова (IMHO).
Кидайтесь скринами, чтобы вас за долбоёбов не посчитали.
Матемач, есть одна штука которая меня давно раздражает. Сам я нихуя не математик, и тервер понимаю исключительно интуитивно, так что сильно подозреваю что я считаю через жопу.
На примере кубика d6. Кидаем его 10 раз, какой шанс что хоть раз выпадет единица?
Я могу это посчитать как 1-(1-1/6)^10 = 0.83849441711, т.е. грубо говоря я считаю шанс что событие не произойдет, и выворачиваю его наизнанку.
И это вот "1-(1-" мне прямо по глазам режет, мой внутренний перфекционист негодует. Как посчитать красиво?
На примере кубика d6. Кидаем его 10 раз, какой шанс что хоть раз выпадет единица?
Я могу это посчитать как 1-(1-1/6)^10 = 0.83849441711, т.е. грубо говоря я считаю шанс что событие не произойдет, и выворачиваю его наизнанку.
И это вот "1-(1-" мне прямо по глазам режет, мой внутренний перфекционист негодует. Как посчитать красиво?
Анализ в широком смысле слова - это, в частности, топология.
x^2+ax=y^2+bx
Как искать площадь такого типа окружностей через интеграл?
Как искать площадь такого типа окружностей через интеграл?
>Как искать площадь такого типа окружностей через интеграл?
Руками.(довести до полных квадратов)
Какие типы задач лучше поручать компьютеру и каким-то системам компьютерной алгебры?
А что относиться к твоему определению такой серьезной математики? Кольца какие-то, теория категорий, вот это всё?
И какое это имеет отношение к обсуждаемой функции? Попробуй потоньше.
Не знаю куда писать, напишу сюда.
Вот я видел в каких-то учебниках аксиомы для вещественных чисел, мол любое множество, объекты которого им удовлетворяют будет множество вещественных чисел, т.е. в аксиомах о свойствах каких-то абстрактных объектов речь идет, а ты их интерпретируй как-нибудь и смотри, что получится.
Также с аксиомами в геометрии получается, объекты конкретные не даны, ты их интерпретируешь, сам решаешь, что понимать под точками, прямыми, плоскостями и т.п.
А вот аксиомы Пеано как надо понимать? Вот там, скажем, первая: "1 является натуральным числом". А один-то - это что такое? Если как выше, то она просто говорит, что в нем есть какой-то произвольный элемент, который обозначили единицей, т.е. множество непустое, но явно же она не про это, блджад!
И еще, где можно найти полный учебник Тао по анализу?
Вот я видел в каких-то учебниках аксиомы для вещественных чисел, мол любое множество, объекты которого им удовлетворяют будет множество вещественных чисел, т.е. в аксиомах о свойствах каких-то абстрактных объектов речь идет, а ты их интерпретируй как-нибудь и смотри, что получится.
Также с аксиомами в геометрии получается, объекты конкретные не даны, ты их интерпретируешь, сам решаешь, что понимать под точками, прямыми, плоскостями и т.п.
А вот аксиомы Пеано как надо понимать? Вот там, скажем, первая: "1 является натуральным числом". А один-то - это что такое? Если как выше, то она просто говорит, что в нем есть какой-то произвольный элемент, который обозначили единицей, т.е. множество непустое, но явно же она не про это, блджад!
И еще, где можно найти полный учебник Тао по анализу?
Она именно про это. Ты всё правильно понял.
>аксиомы Пеано
Триггеред
Пойду читать "Основы анализа"
В чем суть изучения геометрии и геометрии вообще?
Ни в чём.
Почему так? Да и я больше спрашивал об опыте, подходе и всем таком.
Бери да изучай, в чём суть, как такое ответить? Подходы разные, геометрии тоже, опыт берёшь задачи решаешь вот тебе опыт.
У тебя квадратный корень из отрицательных не извлекается, дурочка.
Там комплексное число будет. Он тебе кинул функцию в R. И ты это понимаешь.
Почему не могут договориться о признании нуля натуральным числом?
Зачем нужны какие-либо аксиомы, кроме аксиом теории множеств?
всем привет! можете подсказать, где почитать про пределы от двух переменных и в целом про функции от двух переменных? методички, быть может, брошюры.
Я у него спросил, будет ли функция y = sqrt(x) функцией. Он сказал что да, а на вопросы, что sqrt(4) = 2, -2; начал маняврировать, сказав что это функция задана на числах >= 0, и область значения её так же только >= 0. Хотя определение квадратного корня из числа a: такое b, что b2 = a, он игнорирует.
Потому что старым пидорасам сложно переучиваться видите ли мы не с 0 начинаем счёт, а у нас гуманизм, усыпить их нельзя.
На вещественных числах область значений действительно >=0.
Корень чётной степени из отрицательного числа не существует в области вещественных чисел, поскольку при возведении любого вещественного числа в степень с чётным показателем результатом будет неотрицательное число.
>не существует в области вещественных чисел
Почему вы по дефолту думаете про R? Почему не про Z? Так можно сказать, что корня из 2 тоже нет. Так что не маневрируй.
b = sqrt(a), если b2 = a;
sqrt(4) = 2; -2; потому что (-2)2=22=4
Для Z тоже самое будет. Суть в том, что есть арифметический корень и алгебраический, гугли. sqrt(x) это арифметический корень, sqrt(4)=2.
Арифметический корень
Корни чётной степени определены, вообще говоря, неоднозначно, и этот факт создаёт неудобства при их использовании. Поэтому было введено практически важное ограничение этого понятия.
Арифметический корень n-й степени из неотрицательного вещественного числа a — это такое неотрицательное число b, что bn=a. Обозначается арифметический корень тем же знаком радикала.
Таким образом, арифметический корень, в отличие от ранее определённого (алгебраического), определяется только для неотрицательных вещественных чисел, а его значение всегда существует, однозначно и неотрицательно. Например, квадратный корень из числа 4 имеет два значения: 2 и -2, из них арифметическим является первое.
Если ты погромист и у тебя sqrt(x) = арифм. 2 корень, то это твои проблемы.
Я нигде не писал, что это арифм. 2 корень. И вообще не вижу смысла разделения корня на алг. и арифм. в математике. В других науках, возможно, это и имеет смысл, не знаю.
У всех sqrt(x) арифметический корень, погромисты тут не при делах. Смысл большой, так как функция y-sqrt(x) это функция для арифметического корня, для алгебраического функции быть не может.
>In mathematics, a square root of a number a is a number y such that y2 = a; in other words, a number y whose square (the result of multiplying the number by itself, or y⋅y) is a. For example, 4 and −4 are square roots of 16 because 42 = (−4)2= 16.
Из википедии.
>У всех sqrt(x) арифметический корень
А ещё у всех 0 - не натуральное число, и хули?
Кто-то уже похожим вопросом задавался. Мы тут о функциях же говорим,так что подразумевается арифметический корень.
>и хули?
Откуда я знаю. У меня, кстати, тоже 0 не натуральное.
Ну нихуя, целый 1 человек задавался!
>так что подразумевается арифметический корень
ТЫТОКСКОЗАЛ?
>У меня, кстати, тоже 0 не натуральное.
Натуральные числа - классы эквивалентности по отношению равномощности. Класс с пустым множеством соответствует нулю.
Тут сказано, что если ты используешь значок радикала, то ты уже говоришь о ptincipal square root.
Зачем ты мне русскую вики кинул, если сам используешь английскую? В русской вики и 0 не натуральное число, давай уже определимся.
В английской нет статьи о радикале.
>В русской вики и 0
Там написано, что есть 2 подхода - Бурбаков и мумий. У мумий 0 - не натуральное.
В той же статье из которой ты копипастил есть определение конкретное. В русской есть арифметический и алгебраический корни.
Там неправильно.
Где? В англовики? А нахера ты мне русский учебник показываешь? Разные терминологии и подходы, блядь, анон, ты запарил уже, говорить надо в одной терминологии, если пользуешься англовики скидывай англоучебники и тд
И вообще, если там неправильно, зачем ты тогда оттуда копипастишь? Короче, положняк такой, есть два алгебраических корня из 4: sqrt(4) и -sqrt(4), y=sqrt(x) это функция, её область определения и область значений >=0.
Там половина норм, остальное для неосиляторов.
В анг. книжках выше школо-уровня sqrt(x) многозначна обычно римановы поверхности начинают рассматривать как раз с этой функции.
Дай ссылку. Сомневаюсь, как раз sqrt и должна быть однозначна, слишком много где применяется в таком смысле. Риманова поверхность это C же.
Я тебе сказал, где она многозначна. Сам ищи.
Ты сказал, тебе и карты в руки. В противном случае ты пустослов, таковы правила, не я их придумал.
Ссал и срал я на ваши правила. Открой любую книгу где есть римановы поверхности, высок шанс что там для примера будет рассмотрена функция y = sqrt(x).
Бремя доказательства лежит на доказывающем. Ты же не хочешь сказать, что я не ошибся с пикчей?
И вообще, причём тут комплексные многобразия к R. Про С я тебе ещё в первом посте сказал.
>Бремя доказательства лежит на доказывающем
Ты понимаешь, что это сродни что-то типа "Не служил - не мужик"?
Нет, это не так. И не нужно тему переводить. Пруфы или слив засчитан, зелёная толстая манька.
Перекат!
Я не стал задавать треду какую-то тематику, поскольку эта традиция давно себя изжила. Еще со времен /sci мало кто обращал внимание на заявленный топик. Пусть у начинайко-тредов будет максимально укороченная паста и одинаковое лого. Так любой анон сможет сделать перекат вовремя без каких-либо заморочек. Саму пасту для удобства я поместил в отдельный пастебин: https://pastebin.com/adMijg8Z
Новый пастебин с архивом всех начинайко-тредов: https://pastebin.com/JJN7jsVC
Я не стал задавать треду какую-то тематику, поскольку эта традиция давно себя изжила. Еще со времен /sci мало кто обращал внимание на заявленный топик. Пусть у начинайко-тредов будет максимально укороченная паста и одинаковое лого. Так любой анон сможет сделать перекат вовремя без каких-либо заморочек. Саму пасту для удобства я поместил в отдельный пастебин: https://pastebin.com/adMijg8Z
Новый пастебин с архивом всех начинайко-тредов: https://pastebin.com/JJN7jsVC
Поправочка
Архив: https://pastebin.com/PMvY34XF
Паста: https://pastebin.com/AriH3bdz
Моча, исправь ссылку на архив в 30-ом




























































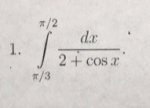



























Если ты школьник или студент, и тебя есть задача, то в здесь тебе помогут её решить или хотя бы скажут, в каком направлении двигаться для её решения.
Только учти, математики - люди ленивые, и никому не интересно решать элементарные первокурсные задачи за просто так. Поэтому если ты просто запостишь в тред условие с комментарием вида "срочна памагити ришить", то тебя скорее всего проигнорируют или отправят читать учебники. Чем более чётко и конкретно ты опишешь суть своих затруднений, тем выше твой шанс на содержательный ответ.
Альтернативный тред для начинающих с жесткой модерацией:
Обсуждение ВУЗов и математического образования:
Мемы сюда:
Классический список литературы
http://pastebin.com/4iMjfWAf
Список книг с dxdy, рекомендованный тамошними обитателями
http://pastebin.com/4FngRj6n
Форчановский список (на английском)
http://4chan-science.wikia.com/wiki/Mathematics
Архивы тредов
В /sci:
https://pastebin.com/w1nJGYv4
Для начинающих:
http://pastebin.com/kiRZGVHW
http://arhivach.org/thread/233955/ 26
https://arhivach.org/thread/251944/ 26.5
http://arhivach.org/thread/251945/ 27
http://arhivach.org/thread/251970/ 28
Хорошие, годные ресурсы:
http://gen.lib.rus.ec/
http://mathprofi.net/
http://www.fmclass.ru/
http://math.stackexchange.com
http://sci-hub.cc/
Ещё линки смотри в треде ссылкоты
Тематикой 29-го треда буду различные математические истории и анекдоты.
Если вспомните что-нибудь интересное постите тут. Я начну:
Один из самым трудных томов трактата Бурбаки – том, посвящённый интегрированию (мере Хаара). Жану Дьёдонне, самому рьяному критику очередной рукописи этого тома, в конце сороковых годов было поручено написание очередной версии. Дьёдонне, в то время находившийся в расцвете своих творческих сил, забросив на целый год всю свою собственную математическую работу, полностью отдался этому нелегкому труду.
Через год, к назначенному сроку, он привез на бурбаковскую виллу на Средиземном море 12 (по числу членов группы) экземпляров своего труда. Первое обсуждение произошло на следующий вечер. Сидели в удобных креслах в большой гостиной, потягивая (в то время ещё не самое лучшее) красное вино и глядя на уютно разгоревшийся камин. Выступали поочередно, причем тон выступлений, неожиданно для гордившегося своим детищем Дьёдонне, был резко критическим. Первое же выступление завершилось такой оценкой: «Место этому уроду – здесь!», после чего помятые машинописные листки рукописи, с тщательно вставленными от руки формулами, были отправлены в камин. И так завершились все одиннадцать выступлений. Обиженный Дьёдонне удалился в свою комнату, где на письменном столе к счастью оставался последний, его собственный, экземпляр рукописи.
Можно представить себе его ужас, когда вместо рукописи он обнаружил там лишь маленькую кучку пепла и записку: «Здесь покоится прах последнего урода Дьёдонне».