Как опровергнуть аксиому выбора? Что можно почитать на эту тему
Как доказать лемму Цорна без аксиомы выбора? Что можно почитать на эту тему
Библию
Не умею упрощать квадратные (и не только) корни. Помогите.
Помогите, плиз, с разобраться пикрил.
Знаю, что в результате получится f(x) = 0, f(x) = x - 1, f(x) = 1 - x, но не знаю, как к этому прийти. :c
Знаю, что в результате получится f(x) = 0, f(x) = x - 1, f(x) = 1 - x, но не знаю, как к этому прийти. :c
Прочитай ещё раз.
Решение на сайте имо
ебаноид недоделанный, я же тебе в предыдущем треде ответил
читать ветку нужно было
благодарю
Найти хотя бы одну функцию (в общем виде) u=f(k), такую что:
1. D(u) ∈ (0; 1)
2. R(k) ∈ R
3. ∃! t : u`(t) = 0
1. D(u) ∈ (0; 1)
2. R(k) ∈ R
3. ∃! t : u`(t) = 0
Опечатка.
Найти хотя бы одну функцию (в общем виде) u=f(k), такую что:
1. R(u) ∈ (0; 1)
2. D(k) ∈ R
3. ∃! t : u`(t) = 0
Сложно.
1/2 Exp[-x^2]
Как доказать, что все гомотопические группы S^n тривиальны?
Спроси у маляра, который жонглёр. Он сейчас где-то в Индии тусуется.
Как показать, что образ гомоморфизма не обязательно нормальная подгруппа без конкретных примеров? Придумал ϕ:H↪G, где H не является нормально подгруппой G, но конкретность данного решения меня бесит...
Напрасно: чтобы доказать, что чего-то не бывает, надо так и делать -- предъявлять пример, когда не бывает
Так как раскладывать функцию в ряд? Вот функция логарифма натурального. Как её разложить в ряд? Я из примеров из книжекнихуя не понял.
Уже мозги кипят, не знаю как подступиться к этому, словно какие-то заклинания, которую не пойми как зазубрить.
Тяжело даются логарифмы в плане осмысления. Где можно почитать про доказательства операций над логарифмами?
Прям совсем строго - только в курсе матана после не малого формализма. Чтобы понять логарифмы, порешай чуть-чуть заданий из Сканави в соответствующей теме. Там есть пара страниц со вступительной информацией.
Это на самом деле зависит от верности исключённого третьего. Если оно верно, то образ гомоморфизма всегда является нормальной подгруппой.
Исключенное третье уже конструктивно опровергнуто. Луркай на архиве
Ну, это понятно. Я про то, что индукция и исключающее третье доказано, что не верно.
А, то есть арифметика Пеано противоречива? Я догадывался об этом уже давно. Ничего удивительного.
Как же надоело зубрить математику...
> зубрить
> математику
С чего начать изучать диффуры и интегралы?
Дифуры с книжки арнольда. Интегралы с курса Зорича
мне кажется, что книга Арнольда слишком жестокая для человека, окончивший 9й класс, и который хочет заняться диффурами
А что делать, если ты не слишком сообразительный? Я же школьную еще не закончил.
с другой стороны, надо же ему как-то осознать, что диффуры и интегралы это не просто набор алгоритмов, как переменные разделить или по частям ебануть. Пусть хоть мельком увидит, как бывает
А у меня вот вопрос к математикам: вы помните все эти теоремы, которыми забиты учебники или вы по-надобности можете их самостоятельно выводить?
Мне кажется, диффуры слишком жесткие для человека, окончившего 9 классов, и не умеющего находить интегралы. Серьезно, для понимания нужен матан первого курса
все, понял. Ты перепутал диффуры и дифференциалы
в чём отличия?
нет, просто я уже прошёл курс тригонометрии, логарифмов, мне хотелось бы пойти дальше, к диффурам и интегралам. смысл задерживать до 1 курса, если есть желание?
Иди, но для дифуров у тебя мало знаний, а для матана как раз
по-твоему откуда брать знания для дифуров? -_-
я ведь для этого сюда и обратился, чтобы мне посоветовали
Для диффуров -- из матана. Их обычно считают разными предметами
из матана - это обширное понятие. конкретизируй, а то мне кажется, что меня здесь возненавидят.
Диффуры = Дифференциальный уравнения - уравнения с производными
Матан = Математический анализ - пределы, производные, интегралы
Аноны, объясните, что за магия происходит при дифференцировании квадратичной функции? Насколько я понимаю, должно быть что-то типа dq(x) = d(x, Ax) = (dx, Ax) + (x, dAx). Как получается то, что получается на пике?
Как быстро, лениво и для не слишком сообразительных освоить школьную математику, особенно геометрию?
Нужно найти фокус произвольного куска параболы. Как это сделать?
Никак
Доказано, что это невозможно
Экстраполяцией. /thread
А если с помощью аксиомы выбора попробовать?
Ну тогда без индукции не обойтись, а это уже не геометрия, а математика.
Ты хотел сказать религия?
Опиши мне как.
Как заставить себя учить математику?
Вопрос надо не стоит. Конечно же, надо и математика используется везде.
Вопрос надо не стоит. Конечно же, надо и математика используется везде.
Никак, оставайся в говне.
Бамп. Как правильно дифференцировать скалярное произведение? Почему получается Adx, а не dAx?
Через лемму Цорна
Опиши мне задачу, как она есть
Задача - доказать аксиомы выбора не используя ничего кроме евклидовой геометрии.
Тащемто такое можно только трюком проделать. Гугли: трансиндукция
Как доказать, что в каждой категории есть объект натуральных чисел?
У тебя в задачнике, видимо, опечатка. Правильнее задуматься, как доказать, что в каждой категории нет объекта натуральных чисел
Кажется, я совсем поехал. Дифференциал линейного оператора — это и есть этот самый линейный оператор: dAx = Adx, ибо A(x+h) - A(x) = A(x) + A(h) - A(x) = A(h). Всё верно, аноны?
Где-то доказано, что я не прав?
Двач, поясни за абсолютное число.
Правильно, что |x| - это может быть одновременно нуль, положительное число и отрицательное число.
То есть, если задаче пишут: отметьте на оси х, |x| = 2, то отметиться -2 и +2 на ней. Или, отметьте точки |x| больше и равно 5, то точки будут: от -5 до 0, и от 0 до 5?
пикрандом
>отметьте точки |x| больше и равно 5
Опечатался - меньше.
Если выразить заданное условие как предикат, то при P(1) и, соответственно, n=1, выражение приобретёт значение 0, делимость которого на три мне непонятна и не относится к теме задачи, значит, построение доказательства по индуктивному методу невозможно. Так ведь?
Сформулирую немного по-другому свой вопрос: корректно ли считать, что "0 делится на Х", если результатом выражения является 0, или нет?
Ноль кратен любому числу по определению делимости, значит, корректно.
Сам написал, сам ответил. Извините, я просто умственно неполноценный
Очевидно, что да. Следует из доказательства аксиомы выбора Гёделем в 30х.
я ссаный гумус и мне нужно название и желательно хайрез фото учебника матана (матана ли?), который проходят в 1-2 семестрах на технических специальностях, CS, вся хуйня. по сюжету персонаж должен всё лето дрочить этот учебник. в сосничестве меня триггерил мордкович до пены изо рта, нужен примерно такой эффект. спасибо
1. Смотришь на оп-пик.
2. Выбираешь любую книжку.
3. Идёшь на libgen.io
4. Скачиваешь.
5. Делаешь скриншот.
Пора ли начинать банить за загаживание треда постами навроде этого?
y''+a^2y=e^2x
y(2) = 6
При каких a эта система имеет единственное непродолжаемое решение?
Я так понимаю, это не задача Коши, т.к. нужно еще начальное условие на первую производную.
Вопросы следующие.
Работает ли здесь теорема о единственности разрешения любой задачи Коши, при некоторых условиях? Здесь вроде как все непрерывно, поэтому можно сказать, что решения всегда будут и их всегда будет бесконечное кол-во, т.к. можно поставить бесконечное кол-во задач Коши. Применимы ли здесь эти рассуждения?
Начнем решать в лоб.
Решение имеет вид С1e^(2x), т.к. 2 - точно не решение ур-я b^2+(a^2)*b = 0
Подставляем, находим C1=1/(2+a^2), отсюда по начальному условию находим a. Но тогда это прямо противоречит моим рассуждениям о задаче Коши, т.к. только в этом случае есть хоть какое-то решение.
Помогите.
y(2) = 6
При каких a эта система имеет единственное непродолжаемое решение?
Я так понимаю, это не задача Коши, т.к. нужно еще начальное условие на первую производную.
Вопросы следующие.
Работает ли здесь теорема о единственности разрешения любой задачи Коши, при некоторых условиях? Здесь вроде как все непрерывно, поэтому можно сказать, что решения всегда будут и их всегда будет бесконечное кол-во, т.к. можно поставить бесконечное кол-во задач Коши. Применимы ли здесь эти рассуждения?
Начнем решать в лоб.
Решение имеет вид С1e^(2x), т.к. 2 - точно не решение ур-я b^2+(a^2)*b = 0
Подставляем, находим C1=1/(2+a^2), отсюда по начальному условию находим a. Но тогда это прямо противоречит моим рассуждениям о задаче Коши, т.к. только в этом случае есть хоть какое-то решение.
Помогите.
>|x| - это может быть одновременно нуль, положительное число и отрицательное число.
То как ты сформулировал - нет. Все числа либо положительные, либо отрицательные, либо 0.
В примерах задач все так
Нужно сделать параболический солнечный коллектор диаметром один метр с фокусом находящимся на расстоянии 9.7 метров от ближайшей к директрисе точки параболы
Спасибо.
А если модуль будет с минусом |-x|, например |-5|, то при задаче, отметьте на оси х модуль |-5| будет = 5, и отметиться от -5 до 0 и от 0 до 5? Или только слева от нуля, с минусом?
Модуль - это число. Когда говорят отметить модуль, подразумевают, отметить точку, соответствующую этому числу. Поэтому отмечай только точку 5. Если тебя просят отметить точки |x| < 5, тебе надо отметить все такие точки, что их модуль меньше 5. Это, конечно, интервал (-5, 5)
А модуль над кольцом?
Вечер в тред, матананы!
Решил угареть по физике, но понимаю, что без матемакики никуда.
Хотел у вас вопросить, какой минимум математики хочу повториь/заполнить пробелы нужен для общей физики понимаю, что я не первый, кто может интересоваться, но в жопе засвербило, прям пиздец. начальная школьная физика, вроде не так мудрена, но вот взглянув на старшие классы и дальше, увидев там обилие математики , немного приуныл от осознания, что чего-то не помню, чего-то не знаю ?
Желательно в литературе, чтобы было куда нырять с места в карьер.
Решил угареть по физике, но понимаю, что без матемакики никуда.
Хотел у вас вопросить, какой минимум математики хочу повториь/заполнить пробелы нужен для общей физики понимаю, что я не первый, кто может интересоваться, но в жопе засвербило, прям пиздец. начальная школьная физика, вроде не так мудрена, но вот взглянув на старшие классы и дальше, увидев там обилие математики , немного приуныл от осознания, что чего-то не помню, чего-то не знаю ?
Желательно в литературе, чтобы было куда нырять с места в карьер.
Для начала учись доказывать аксиому выбора. Без этого сегодня в физике никак.
Для теории поля очень понадобится индукция. Для интереса можешь посмотреть трансфинитную индукцию
Зельдович, Яглом. "Высшая математика для начинающих физиков и техников". Название говорит само за себя. Зельдович - гениальный советский физик, Яглом тоже известный человек.
Ценю, то что написано, но это рановато пока что.
Я спросил про мат. литературу, которая поможет мне понимании тех или иных вещей, по этому попросил список литературы, чтобы школьную программу старших классов и первых-вторых курсов вузов по математике.
Ох! не видел ранне, благодарю!
Я лично с этого начинал, тебе тоже могу посоветовать.
Kurt Gödel, 1931, On the Axiom of Choice and its various proofs. Vol. I.
Репетитор?
Зарепорчен, скрыт проклят и заставлен решать несобственные повторные интегралы по контуру.
спасибо
Анон, хелп, здесь же куча спецов по дифурам.
Чуть больше счетного числа, но еще не континуум
Как учить математику?
Читаешь учебник, смотришь лекции, делаешь упражнения.
> Principles of Learning a Mathematical Discipline
> If you have not had the prerequisites in the last two years, retake a prerequisite. The belief that it will come back quickly has scuttled thousands of careers.
> Study every day – if you study less than three days a week, you are wasting your time completely.
> Break up your study: do problems, rest and let it sink in, do problems; work in a comfortable environment.
> Never miss lecture.
> Remember, even if you are able to survive by cramming for exams, the math you learn will only go into short term memory. Eventually, you will reach a level where you can no longer survive by cramming, and your study habits will kill you.
Сначала учишься доказывать вещи по индукции. Говорят это очень полезно, много всего можно доказать.
Посоны, хочу задрочить матан прямо пиздец, но увы, мерзкая учительница в школе скатила меня из отличника в трочники, а ещё более мерзкая преподша в универе вообще убила нахуй желание и я отчислился из-за ебучего вышмата. Теперь я поумнел и хочу перепоступить, для этого надо учить эту мерзкую математику, поясните как вкатиться полному ньюфагу, застрявшему на уровне 7 класса
Можно по-русски пожалуйста
Как доказать, что существует уникальное отображение φ : ℝ → ∅?
Существование я ещё хоть как-то представляю, но вот уникальность вообще никак.
Существование я ещё хоть как-то представляю, но вот уникальность вообще никак.
Трахни сына этой учительницы
А что такое уникальное отображение, что-то такого понятия не встречал.
Модульный дед, ты ебанулся там?
Удали все элементы из непустого
Это неконструктивно
Удали из конечного
Все равно аксиому выбора придется использовать
В моей аксиоматике можно спокойно доказать, что аксиома выбора неверна.
Доказано, что такой непротиворечивой аксиоматики нет. Ищи ошибку
Для чего?
Доказано, что аксиома выбора независима от уёбищной ZF. Про мою систему Гёдель и Коэн ничего не доказывали.
Если исключённое третье не верно, то из этого легко следует, что и аксиома выбора неверна.
Такое чувство что доска находится под мощнейшим тролингом девятикласника, который пытается тролировать аксиоматикой.
Не могу найти формулу н челна последовательности для шестого задания и ответы с 11 по 22 не сходятся с ответами учебника.
Поясните что и почему.
Поясните что и почему.
Там и без индукции все просто. Вынести n за скобки, расписать разность квадратов. Получится (n-1)n(n+1). Из трех последовательно идущих натуральных чисел хоть одно делится на 3.
В шестом каждое число = 1 + 2 + 3 + 4...
В 21 сходится к нулю, в 22 расходится к бесконечности. Возьми лучше задачник с решениями, русофоб.
В шестом арифметическая прогрессия второго порядка. Смотри пикрел, составляй систему уравнений и находи коэффициенты
Модульный дед, тебя не заебало с самим собой пиздеть?
Скажите, каким уравнением описывается круг? Не окружность, а именно круг, т.е. каждая точка внутри окружности?
x^2+y^2<r^2
>Не могу найти формулу н челна последовательности для шестого задания
a(n)=n+Sum(n-1), где Sum(n-1) - сумма первых (n-1) чисел ( как ты помнишь Sum(n)=(n x (n+1))/2 )
Кажись так.
> дед
Кстати, почему?
Хорошо.
9 сходится на бесконечность
10 к одному
11 к минус бесонечности
12 на минус плюс бесконечность и предела не имеет
13 к нулю
14 к бесконечности
15 к бесконесности
16 к бесконечности
17 к бесконечности
18 к одному
19 к одному
20 к 3/2
21 к нулю
22 к бесконечности
Все правильно?
>11 к минус бесонечности
к 1
>каким уравнением описывается круг
неравнество. Уравнением, мне кажется, описать не получится.
>11 к минус бесконечности
С чего ты взял? К 1 же.
https://math.stackexchange.com/questions/29578/is-there-a-way-to-represent-the-interior-of-a-circle-with-a-curve
Бля, ты наугад ебошишь? Это надо доказывать по определению. У тебя несколько неверных ответов. Если ты просто выписываешь первые несколько членов и пытаешься угадать, ты что-то делаешь не так
Как так?
Делим все члены на n, получаем 1-n/1-(~0)
Сначала нужно преобразовать к виду
x 1 lim (1) 1
lim ---- = lim ------------ = --------------------- = ----- = 1
x+1 1+( 1/x) lim (1) + lim (1/x) 1+0
Какие американские школьные учебники по математике являются самыми лучшими сегодня?
в знаменателе первая 1 идёт, а не x , сорри за ошибку.
И да
>18 к одному
Почему? Там же к 1/2 .
Это как так преобразовать надо? Я тупо в квадрат все возвел.
Да, нужно умножить на (sqrt(x2+x) + x)/(sqrt(x2+x) + x), тут sqrt - квадратный корень из (x^2-x).
А если тупо в лоб посчитать тоже около 0.5 получится...
Да, для больших чисел получается около 0.5.
Магия блядь
Если ты еще не понял, насколько велики твои проблемы, в №19 должно быть = 1/е, где е - это https://ru.wikipedia.org/wiki/E_(%D1%87%D0%B8%D1%81%D0%BB%D0%BE)
Помогите умственно отсталому с дискретной математикой. Чисто абстрактно не могу понять, что такое класс эквивалентности.
Вот есть у меня множество А, пусть там будут "петухи". Я задаю на него эквивалентное отношение по такому-то предикату (допустим, "петух x зашкварил петуха y") - пусть это будет множество упорядоченных пар xRy.
Отношение xRy эквивалентное по определению - оно:
1) Рефлексивно (петух x шкварит сам себя тем, что прикасается к себе)
2) Симметрично (верно и обратное -- петух y также шкварит петуха x, когда они друг-друга трогают)
3) Транзитивно (x трогал y, а y трогал z: получается, x зашкварил петуха z своими хуиными молекулами через петуха y)
Известно, что отношение эквивалентности на множестве А задаёт на нём разбиение. Я не понимаю, как оно так получается. Что имеем: множество "петухи" A и его эквивалентное отношение "шкварные петухи" извините за тавтологию. Вопрос:
1) Класс эквивалентности является чем? Отдельным подмножеством xRy? Что это за z на ОП-пике, зачем он? Разбиение zRx соответствует разбиению xRy из моего примера? Классы эквивалентности являются блоками разбиения? Реально просто не понимаю, что такое Е(x) даже с формальной точки зрения.
Вот есть у меня множество А, пусть там будут "петухи". Я задаю на него эквивалентное отношение по такому-то предикату (допустим, "петух x зашкварил петуха y") - пусть это будет множество упорядоченных пар xRy.
Отношение xRy эквивалентное по определению - оно:
1) Рефлексивно (петух x шкварит сам себя тем, что прикасается к себе)
2) Симметрично (верно и обратное -- петух y также шкварит петуха x, когда они друг-друга трогают)
3) Транзитивно (x трогал y, а y трогал z: получается, x зашкварил петуха z своими хуиными молекулами через петуха y)
Известно, что отношение эквивалентности на множестве А задаёт на нём разбиение. Я не понимаю, как оно так получается. Что имеем: множество "петухи" A и его эквивалентное отношение "шкварные петухи" извините за тавтологию. Вопрос:
1) Класс эквивалентности является чем? Отдельным подмножеством xRy? Что это за z на ОП-пике, зачем он? Разбиение zRx соответствует разбиению xRy из моего примера? Классы эквивалентности являются блоками разбиения? Реально просто не понимаю, что такое Е(x) даже с формальной точки зрения.
Это зависит от твоих конкретных аксиом, более конкретно это зависит от верности или неверности аксиомы выбора.
Лучше бы помог мне. Какие-то аксиомы выбора говоришь, сразу видно, умный человек
Я и пытаюсь тебе помочь, ответ на твой вопрос зависит от статуса аксиомы выбора в твоей системе.
Тут же очевидно, что у него аксиома выбора неверна. Без этого невозможно определить классы эквивалентности.
>Класс эквивалентности является чем? Отдельным подмножеством xRy?
Это независимо от любой непротиворечивой теории множеств.
Можешь добавить аксиому, что он является отдельным подмножеством xRy.
Доказал с помощью трансиндукции. Что дальше, как решать?
Известно, что аксиома выбора и её отрицание ведут к противоречию. Почему же её до сих пор кто-то использует?
Как доказать, что в любой категории имеется начальный или терминальный объект?
Это неверно. Контрпример - категория с одним объектом и двумя стрелками.
Где этот чертов модератор.
Классы эквивалентности петухов - это такие подмножества твоего курятника, среди которых все петухи перешкварили друг друга. Ты подобрал неудачный пример про "петух х зашкварил петуха у". Давай так "петух х одинаково зашкварен как и петух у". То есть если xRy, они либо оба зашкварены, либо оба нет. Теперь внимательно проверь определение эквивалентности. Если a и b одинаково зашкварены, и b и с одинаково зашкварены, то a и c одинаково зашкварены. Так же с симметричностью и транзитивностью. Теперь в твоем курятнике есть два подмножества. Одно состоит из зашкваренных петухов, другое из незашкваренных. Это и есть классы эквивалентности
p.s. надо отдельно доказать, что ты вообще можешь выбирать какого-то петуха из множества
Как доказать, что в любом топосе существует нулевой объект?
Какой самый эффективный способ сконструировать бесконечное количество элементов пустого множества?
Взять защечное пространство и рассмотреть в нем объект залупа.
Как можно показать что существует инъекция из множества вещественных чисел в множество целых чисел? И можно ли это вообще показать?
Что за "объект залупа"? Объект пространства петель?
Можно ли доказать в ZFC, что существуют непустые множества такие, что их декартово произведение пустое?
Можно ли доказать аксиому выбора финитарными методами?
Блять, что за буйство семенов итт?
"Можно ли посрать не снимая свитера?
Можно, но там все через жопу."
"Как доказать что тян не умеют срать?
Они не изоморфны"
Ну что за хуйня?
"Можно ли посрать не снимая свитера?
Можно, но там все через жопу."
"Как доказать что тян не умеют срать?
Они не изоморфны"
Ну что за хуйня?
Поясните за пустое множество в нивной теории множеств. На лекции сказали, что если к множеству добавить пустое множество, то он не изменится. Но ведь в множестве окажется на 1 элемент больше. Ну и что, что этр пустое множество. Или ещё говорили, что если множество состоит только из пустых множеств, то оно пустое и не важно сколько в нём пустых множеств. И при этом на википедии есть такой пример Ø ≠ {Ø}. Почему множество, которое содержит пустое множество не редуцируется до пустого множества как это бы происходило с множеством из одного элемента из которого бы изъяли этот элемент?
Ну это зависит от многих вещей. Если у тебя есть некая функция выбора, то тут всё очевидно.
Про функцию выбора что-то говорили, но я не понимаю, что это значит.
Попробуй сам доказать, что такая "функция выбора" существует всегда. Довольно несложно, но зато очень хорошее упражнение.
Что такое теорема выбора? листал призентацию и кажется нашёл определение функции, но не понял его. Объясни
Теорема выбора (точнее выражение эквивалентное ей) говорит, что декартово произведение любых непустых множеств тоже непустое.
Попробуй доказать это. На твоём первом слайде уже имеется неплохая подсказка насчёт того, как это делать.
Подскажите как доказывать что существует нетривиальный гамаморфизм φ : G → H, где G и H произвольные группы.
Погуглил, что такое декартово произведение множеств. Это вроде очевидно. Если в каждом множемтве есть хоть 1 элемент, то и ы произведении будет минимум 1 элемент. Не знаю как математично доказатб и что с этим делать что понять что такое функция выбора и пустое множество.
гугли ряд тейлора, ну берем мы производную считаем, тут нужно уметь это делать, и подставляем в формулу ряда
А вообще можно ли доказать, что любая абелева группа тривиальна?
Ты неправильно понял лектора. Речь о том, что M∪Ø = M для любого M.
>множество, которое содержит пустое множество не редуцируется до пустого множества
Мешок, в котором лежит синий мешок, - не то же самое, что синий мешок.
Он говорил, что не важно сколько пустых множеств в множестве. Он говорил, что сколько бы пустых множеств мы не добавляли в пустое мнодество оно всё равно будет равно пустому. То есть множество в котором 2 пустых множество равно пустому множеству, но почему-то множество в котором 1 пустое множество не равно пустому.
Это небольшая тонкость, которая возникает при переходе к нормальной теории множеств. Сначала забудь, что ты знал из школы. Теперь пойми, что для объектов/множеств определены два значка:
∈ - Принадлежит
⊂ - Включается
Это две разные вещи (а именно бинарные отношения). Теперь введем краткую запись:
а, б, с ∈ N <=> N = {a, б, с} (если в N больше нет элементов)
{а, б, с} ⊂ N <=> N = {а, б, с} (если в N больше нет элементов.
Видишь, во втором случае мы имели дело с множеством, а в первом с несколькими элементами. Если во втором случае использовать знак принадлежности, получим:
{а, б, с} ∈ N <=> N = {{а, б, с}}
Если непонятно, перечитай еще раз, внимательно обратив внимание на наличие скобочек. Если все равно не понял, открывай любой учебник по теории множеств или порешай задачи из твоего учебника. Там часто бывает введение про множества
А если а б или с равно пустому множеству, то это считается за элемент?
Пусть M, N - пустые. То есть M = N = Ø
Теперь добавляем:
Ø ∈ M => M = {Ø}
M ∈ N => N = {{Ø}}
Пусть A = B = Ø - пустые
Теперь добавляем:
Ø ⊂ A => A = Ø
A ⊂ B => B = Ø
За элемент можно считать, что угодно
Вряд ли тебе стоит париться над этим.
http://schizomatrix.tk
Вот попробуйте найти в этой шизоматрице по дню рождения успешного математика, которому так не высвечивается успех.
Вот попробуйте найти в этой шизоматрице по дню рождения успешного математика, которому так не высвечивается успех.
Это ты про наивную теорю множеств пояснил?
Любое множество равно пустому множеству.
Это верно и для наивной, и для не наивной. Просто в ненаивной об этом справедливо не запариваются
Спасибо.
Пустое множество -- такая же логическая абстракция, как и число, и справедливо может считаться элементом множества, поскольку множество это совокупность абстракций, мыслимая как некая единая абстракция per se. Тебе лекцию читал дурачок просто.
Мимофеласаф
Дополню это наблюдение примером.
Допустим, есть множество A = {∅}. |A| = 0.
Но, есть множество B = { {∅} }. |B| = 1.
Это так, потому что в множество А входит пустое множество, но множество Б включает в себя другое множество. Для нас не имеет значения, - B мог бы быть { {1, 2, 3} }, например, и его мощность так же равнялась бы единице, потому что подмножество {1, 2, 3} является элементом множества Б, а мы интерпретируем подмножество как элемент множества вне зависимости от того, что это подмножество включает в себя внутри, даже пустое множество.
Мощность A = {∅, ∅, ∅} была бы равна 0, потому что это тавтология с логической точки зрения, но A = { {∅}, {∅}, {∅} } уже равна трём. Как-то так, короче.
Тогда в чём разница {∅} и ∅ если у обоих размер 0?
Безотносительно надмножества - ни в чём.
А попроще. Ведь они не равны.
> Ø ⊂ A => A = Ø
Братан, ну за такие предъявы у нас во дворе бьют лопатой по ебалу.
> Допустим, есть множество A = {∅}. |A| = 0.
> Но, есть множество B = { {∅} }. |B| = 1.
> Это так, потому что в множество А входит пустое множество, но множество Б включает в себя другое множество.
По твоему же первому утверждению видно, что А - пустое, ты сам это сказал. То есть множество, включающее в себя пустое множество, пусто. Следовательно, твое В включает лишь пустое множество, как ты сам написал, а значит пусто. Двойку тебе по логике, школьный недофилософ.
Алсо, беги скорей в /пх, пока тебя тут не забанили.
>Следовательно, твое В включает лишь пустое множество, как ты сам написал, а значит пусто
То, что это множество пусто, не значит, что включающее его множество тоже пусто, понимаш.
Когда мы берём множество P само по себе, оно пусто. Когда мы берём его как элемент другого множества, то то другое множество Q имеет один элемент -- пустое множество P.
Как бы оно внутри себя не имеет элементов, но при этом само является элементом для другого множества.
> Допустим, есть множество A = {∅}. |A| = 0.
Перечитывай, пока не поймешь. Не лезь рассуждать о том, в чем не шаришь. Пришел задавать вопросы - задавай.
>Не лезь рассуждать о том, в чем не шаришь.
Хороший совет.
>Пришел задавать вопросы - задавай.
Почему формула пифагора, а также формула вычисления расстояния между двумя точками, остается справедливой в простраснтвах с любой размерностью?
Потому что пустое множесто по сути это понятие отсутствия чего либо. Отсутствие отсутствия не дает наличия, смекаешь.
Ты дебил что ли?
Мы добавляем к рандомному набору пустоту. Нихуя не изменилось.
А если добавить к рандомному набору три набора пустоты то изменится очень многое.
В математике - по определению. Мы буквально так определяем евклидово пространство, что в нем есть вот такая формула расстояния.
Почему наш физический мир очень похож на евклидовое пространство - вопрос к физике, я хз
Здесь, конечно, слишком вольное следствие. Это все я написал с учетом строк выше, про то, что в А больше нет элементов
Ну все-таки не физический мир похож на евклидово пространство, а the other way around.
Значит то в чем нарушается формула вывода расстояний уже не эувклидовое пространство?
И разве эвклид не вывел свое личное пространство рисуя палочки на песке в реальном мире?
Еще вопрос, почему мы уверенны что функция куба весте растущая?
Может на каком то числе где то в районе плюс бесконечности она к хуям уходит на минус бесконечность.
Может на каком то числе где то в районе плюс бесконечности она к хуям уходит на минус бесконечность.
Математики генерализировали-генерализировали, генерализировали-генерализировали, да не догенерализировали.
С палочками на песке одна формула, с шариками в пространстве - чуть другая, но похожая. Хм, а что если нам вывести общую формулу для пространств любой размерности, которая бы сохраняла привычные нам свойства уже известнвх нам формул, а сами эти уже известные формулы являлись бы ее частными случаями? Хм!
Потому что индукция.
Но почему именно квадрат? Почему не куб в трех измерениях, охуллионная степень в бесконечномерном варианте?
> индукция
Работает только на конечном числе случаев и на их основании делает выводы.
Вчаснасти, где доказательтво того что доказательство остается верным для при переходе от n к n+1?
> индукция
>Работает только на конечном числе случаев и на >их основании делает выводы.
На самом деле работает на счетном числе случаев, а на несчетном есть трансфинитная индукция
Ты спрашиваешь формальное доказательство монотонности функции х3? Если вкратце, оно основывается на определении возведения чисел в степень. В нормальных учебниках матана расписано подробно
Потому что оно основано на свойствах реального мира, а он работает именно так, написали ведь уже. Можно определить другую дистанцию, без квадратов, если хочется.
Или: потому что расстояние нам нужно неотрицательное, и чтобы от перестановки точек местами расстояние не менялось. Посиди и попридумывай такие функции расстояния, которые отвечали бы этому критерию.
Ну давай ты уже возьмешь учебник матана за 10 класс и почитаешь, что такое доказательство по индукции, мммкей?
Посоветуйте школьнику мне литературу, чтобы начать нормально разбираться в математике. Чтоб правила/формулы описывали, ну и какой-нибудь сборник задач хороший.
Вам в школе выдали все что нужно.
Но мне хотелось бы изучить что-нибудь более прикладное, чем школьную херню. Тут выше писали про доказательство аксиому выбора, есть что почитать?
Модер вообще собирается чистить? Этот пидор уже все засрал.
Возможно, это разные пидоры?
Как вообще доказывать существование гамалогии?
Семен плес
Дали определение лимита последователтности, что это такое а, где для любого эпсилон верно что внутри интервала а плюс эпсил и а минус эпсил бесконечное количество точек, а за интервалом конечное. Ещё выражение похожее на то, что на пике нарисавали. Потом говорили про монотоные последователтности и супремумы. В конце сказали про фундаментальные последователтности и что-то про коши. Дали список книг, но не в одной из них я не нашёл такого. Поясните из какого раздела математики это было и что почетать чтобы понять то что пытались объяснить?
Абсолютно любое начало матана. Обсуждение учебников матана в соседнем тренде, но мой простой вариант для знакомства - Ильин
Ну, блядь, а - предел последовательности х, если любой интервал, содержащий а, содержит почти все х.
Почти все = все, кроме конечного числа
Фундаментальная последовательность(последовательность Коши), это последовательность рациональных чисел, для которой для любого e>0 найдется отрезок длины e, содержащий почти все члены последовательности.
Читай Шварца, чтобы не быть баттхертом.
Ну вы баттхерты, развели здесь.
Кароче нахуй, смотри. Множество это чёта типа коробки, которой мы можем задать только 1 вопрос -Лежит ли в тебе %хуйня_нейм%? По научнаму это звучит как -Множество задано, если про любой элемент можно сказать, лежит ли он в множестве или нет. От сюда 1 важное следствие, которое часто умалчивается, и где ты сделал ошибку. Т.к. коробка отвечает только есть/нет, то мы не берем во внимание количества чего-то. Например {1,1,1}={1}.
Допустим ты нашел коробку, и она на все твои вопросы ответила, что не содержит %хуйня_нейм%. То есть коробка пуста. То такое множество называется пустым. Если эту коробку положить в другую коробку, назовём её F, то на вопрос, содержит ли F пустое множество F ответит "Ага". Поэтому F не пусто.
Не нужно думать про пустоту и прочую хуергу.
Добавлю про подмножества, где-то несколько месяцев назад 1типочек тут не понимал.
1) Пустое множество является подмножеством любого множества.
Чтобы это понять нужно на определение подмножества посмотреть с другой стороны. Его можно переформулировать вот так: А является подмножеством В, если в А нет элемента, который не принадлежал бы В. Из этого определения легко понятно, что пустое множество это подмножество любого множества, потому что в нем нет элемента, который не принадлежал бы любому множеству.
Надеюсь всё ясно. Я пошёл варить кукурузу.
Кароче нахуй, смотри. Множество это чёта типа коробки, которой мы можем задать только 1 вопрос -Лежит ли в тебе %хуйня_нейм%? По научнаму это звучит как -Множество задано, если про любой элемент можно сказать, лежит ли он в множестве или нет. От сюда 1 важное следствие, которое часто умалчивается, и где ты сделал ошибку. Т.к. коробка отвечает только есть/нет, то мы не берем во внимание количества чего-то. Например {1,1,1}={1}.
Допустим ты нашел коробку, и она на все твои вопросы ответила, что не содержит %хуйня_нейм%. То есть коробка пуста. То такое множество называется пустым. Если эту коробку положить в другую коробку, назовём её F, то на вопрос, содержит ли F пустое множество F ответит "Ага". Поэтому F не пусто.
Не нужно думать про пустоту и прочую хуергу.
Добавлю про подмножества, где-то несколько месяцев назад 1типочек тут не понимал.
1) Пустое множество является подмножеством любого множества.
Чтобы это понять нужно на определение подмножества посмотреть с другой стороны. Его можно переформулировать вот так: А является подмножеством В, если в А нет элемента, который не принадлежал бы В. Из этого определения легко понятно, что пустое множество это подмножество любого множества, потому что в нем нет элемента, который не принадлежал бы любому множеству.
Надеюсь всё ясно. Я пошёл варить кукурузу.
Одно из свойств множества в том, что все эл-ты разные.
Сварил кукурузку. Вкусная очень.
>Класс эквивалентности является чем? Отдельным подмножеством xRy?
Нет. Класс эквивалентности множества А есть подмножество этого множества. z - просто рандомный элемент из А. Запись означает - класс эквивалентности х это множество E таких z из А, что zRx.
>Класс эквивалентности является чем? Отдельным подмножеством xRy?
Нет. Класс эквивалентности множества А есть подмножество этого множества. z - просто рандомный элемент из А. Запись означает - класс эквивалентности х это множество E таких z из А, что zRx.
>если про любой элемент можно сказать, лежит ли он в множестве или нет
Рассмотрим множество цифр, встречающихся в десятичной записи числа пи таким образом, что им точно предшествует подстрока 7776644123. Невозможно сказать, принадлежит ли цифра 4 этому множеству. Но множество, тем не менее, задано.
Короче, Специальная Относительности.
1) Чел стоит на месте, мимо пролетает свет со скоростью света.
2) Чел быстро движется в космическом корабле, мимо в том же направлении пролетает свет со скоростью света (а не меньше, как ожидалось).
3) Чел стоит на месте и смотрит вперёд, берёт фонарик и светит себе за спину. Мимо, со спины прилетает свет (параллельно лучу из фонарика). Через мгновение чел провожает его взглядом.
Скорость света относительно луча из фонарика равна скорости света.
Но луч из фонарика сам движется со скоростью света в противоположном направлении.
А оносительная скорость (друг относительно друга) равна скорости света, а не двум скоростям света, как должно было бы быть.
Но как это возможно? Да проще простого:
одна из скоростей света равна нулю.
И когда один свет пролетает мимо другого, то один из них всегда встаёт, либо скорость их обоих падает в два раза.
Ткань пространства-времени порвалась.
Вселенную распидорасило.
Конец.
1) Чел стоит на месте, мимо пролетает свет со скоростью света.
2) Чел быстро движется в космическом корабле, мимо в том же направлении пролетает свет со скоростью света (а не меньше, как ожидалось).
3) Чел стоит на месте и смотрит вперёд, берёт фонарик и светит себе за спину. Мимо, со спины прилетает свет (параллельно лучу из фонарика). Через мгновение чел провожает его взглядом.
Скорость света относительно луча из фонарика равна скорости света.
Но луч из фонарика сам движется со скоростью света в противоположном направлении.
А оносительная скорость (друг относительно друга) равна скорости света, а не двум скоростям света, как должно было бы быть.
Но как это возможно? Да проще простого:
одна из скоростей света равна нулю.
И когда один свет пролетает мимо другого, то один из них всегда встаёт, либо скорость их обоих падает в два раза.
Ткань пространства-времени порвалась.
Вселенную распидорасило.
Конец.
>Невозможно сказать, принадлежит ли цифра 4 этому множеству
Возможно. Принадлежит.
Сап, не понимаю суть лагорифмов, и вообще почему они обязательно должны быть положительными ?
>почему они обязательно должны быть положительными
ЯСКОЗАЛ, РЯЯЯЯ!!!!!!
Ну не трали.
>почему они обязательно должны быть положительными
>лагорифм
Мы с тобой об одних логарифмах думаем?
Сап, не понимаю суть гамалогий, и вообще почему они обязательно должны быть тривиальными ?
Вопрос к знающим, тут такие были.
Хочу переметнуться в HoTT. Мои знания математики: шире, чем у тебя.
Но я вдруг понял, что за HoTT будущее. С чего начать? Должен ли быть бэкграунд в cs? Какой-нибудь haskell или agda знать обязательно? А coq?
Моя цель в конечном счете - доказательство недоказанного из раздела многообразий Фано.
Хочу переметнуться в HoTT. Мои знания математики: шире, чем у тебя.
Но я вдруг понял, что за HoTT будущее. С чего начать? Должен ли быть бэкграунд в cs? Какой-нибудь haskell или agda знать обязательно? А coq?
Моя цель в конечном счете - доказательство недоказанного из раздела многообразий Фано.
Логарифм это индекс по модулю некоторой небесконечной группы кольца вычетаний, при этом все члены к-го, кроме задаваемой степени, входят в небесконечную абелеву мультипликативную группу.
>Должен ли быть бэкграунд в cs? Какой-нибудь haskell или agda знать обязательно? А coq?
Нет, но если хочешь узнать, как связаны теория типов и языки программирования, то есть серия книг от Benjamin C. Pierce.
>С чего начать?
С книги HoTT или Мартина Лёфа.
А правда, что если граф связный и ацикличный (т.е. "дерево"), то он обязательно антитранзитивный?
А ещё: получается, для связного неориентального графа остовое дерево можно представить таким образом: граф представляется как G=(N, E), где N - множество вершин, а E - множество рёбер. При этом E можно представить как отношение на N. Если из этого отношения убрать все транзитивные хуйни, получится отношение, которое является остовым деревом для G.
Я почему это говорю-то всё: когда мы хотим дополнить отношение до транзитивности, мы так и говорим. А когда мы хотим убрать все xRz, принадлежащие R, при наличии в R пар xRy и yRz -- это как называется? Дополнить до антитранзитивности?
А ещё: получается, для связного неориентального графа остовое дерево можно представить таким образом: граф представляется как G=(N, E), где N - множество вершин, а E - множество рёбер. При этом E можно представить как отношение на N. Если из этого отношения убрать все транзитивные хуйни, получится отношение, которое является остовым деревом для G.
Я почему это говорю-то всё: когда мы хотим дополнить отношение до транзитивности, мы так и говорим. А когда мы хотим убрать все xRz, принадлежащие R, при наличии в R пар xRy и yRz -- это как называется? Дополнить до антитранзитивности?
>Какой-нибудь haskell или agda знать обязательно? А coq?
Haskell противоречивое дерьмо, особого смысла нет изучать. Агду или coq по пути выучишь.
Нужна везде возрастающая функция имеющая асимптотой число 80 на бесконечности.
Как такую функцию с помощью показательной сделать?
Как такую функцию с помощью показательной сделать?
Вот почитал когда-то эссе какого-то математика, мол в школе детей учат красить заборы, а не рисовать и все в таком духе. Есть книшки которые он бы одобрил?
y(x) = 80 + x^(-1)
>y(x) = 80 + x^(-1)
Я, конечно, извиняюсь, но это гипербола, поднятая на 80, она мало того, что не монотонная, так еще и те промежутки, где она монотонна - она убывает.
y = x, x<1
y=80 - (1/x), x >= 1
Двачую, теперь верно. Не так прочитал
Что ты имеешь ввиду под >положительными?
Я придумал только что можно считать через один справа или сверху и будет +1 -1 - таким образом могу заполнить нижний ряд:
2 2 x 1 1 2
Еще заметил закономерность, что через 4 после единицы идет единица - но это бесполезный факт
Где реальное доказательство, что энергия квантуется?
То что основание логорифма должно быть строго больше нуля. Я понимаю почему оно не равно единице, а вот понять почему оно должно быть только положительным не могу
Основание логарифма может быть меньше нуля, но без комплексных чисел далеко не все логарифмы можно будет найти. В реальных числах к примеру нельзя найти log_{-2}(2).
В /sci/. Очевидно же.
самому слабо? физики не знаешь? как жэ ты так физмат?
Ты приходишь в /math/ и требуешь доказать, что энергия квантуется. Но ты делаешь это без уважения.
нужно за два года выучить физику 9-11 класс, с чего начать и чем закончить?
Но энергия не квантуется.
А как с комплексными числами работать? Там же если степень нечетная корни из минус эдиници вылезать будут.
Элементарный учебник физики Ландсберг 3 тома
Репетитор Касаткина 2 части
В 11 классе апнулся с 40 до 92
по егэ
починка
Посните за последовательность коши. Эта та последовательность, у которой разность между верхним пределом и нижним постоянно уменьшается. Типа на пике верхний предел опускается, и нижний возрастает. Из-за этого последовательность сходится. Но то если верхний предел растёт? И при этом и нижний предел растёт, но чуть быстрее. Расстояние между ними со уменьшается, но ничто не мешает им расти бесконечно. Тогда предел у последовательности бесконечность и она не сходится. Такое возможно? Почему?
Поясните за О нотацию. Говорят, что O(2^2n)=O(n^2). Я подозреваю, что тут ошибка, но боюсь ошибиться. Это так или можно доказать?
Поясните за О нотацию. Говорят, что O(2^2n)=O(n^2). Я подозреваю, что тут ошибка, но боюсь ошибиться. Это так или можно доказать?
пик забыл
В математике принято оперировать конкретными определениями. Определения есть у последовательности, сходящейся по критерию Коши, верхнего предела и верхней точной грани. Ты все люто намешал. У О-нотации тоже есть определения.
>Эта та последовательность, у которой разность между верхним пределом и нижним постоянно уменьшается
нет
Ты хотел сказать не "верхний предел", а верхняя точная грань, но это все равно не тоже самое, что и критерий Коши.
>Такое возможно? Почему?
Да, потому что ты не так понял критерий Коши.
>Это так или можно доказать?
Если я правильно понял запись, это не так. Мб ты что-то не так написал. Можно доказать по определению
Поясни про растущую вверх последовательность коши.
Записал я правильно. Там ещё 2^n квадратичной назвали. Скорее всего ошибка.
Бля чел, вот такая хуйня в каждом посте. Я не могу пояснить короче чем определение из вики, и не могу привести пример понятней, чем в любом учебнике. Можешь разобраться с этим за полчаса, если знаешь определение предела, а можешь ждать здесь месяц, пока поймешь, что никто это не разжует для тебя
Я же частный случай спрашиваю. В общих чертах понимаю.
Анон, а ты тоже оргазмируешь, когда прикасаешься к математической книге?
Зависит от книги, но обычно да.
Нет, ибо мне надо читать элементарщину.
Нет, у меня все книги - электронные.
моар
Это с текущего мат. треда на 4chan. Там почти всегда на оп-пиках 2д тян с мат. книгами
там же мат-треда нет, только /sci/
Мат-борды нет, а тред есть, как раз на /sci/.
Что такое дифференциал?
На викисрачие написано, что это - линейная часть приращения, но что такое "линейная часть"? Зачем под интегралом пишут дифферинциал? училка в шкальне сказала, что его там ставят чтобы указать, какую переменную интегрируют
На викисрачие написано, что это - линейная часть приращения, но что такое "линейная часть"? Зачем под интегралом пишут дифферинциал? училка в шкальне сказала, что его там ставят чтобы указать, какую переменную интегрируют
пиздишь, не нашёл
Дифференциал - это прямой образ гладкого отображения относительно функтора взятия касательного пространства. То, что стоит под знаком интеграла, - это не дифференциал, а дифференциальная форма. Формулировки вроде "линейная часть приращения" имхо довольно вредные (мне они сильно помешали разобраться в своё время), хотя и не совсем бессмысленные. Если ты школьник, то тебе такая наверное сойдёт, но тогда знай, что здесь ты чего-то сильно не понимаешь
Линейная часть приращения - это когда ты функцию раскладываешь в ряд тейлора и берёшь линейный член (т.е. забиваешь на все степени переменной выше двух включительно). Линейная часть приращения - эта линейная функция, которая приближает твою исходную функцию наилучшим образом (в фиксированной точке). Подобно тому как касательная наилучшим образом приближает кривую (в фиксированной точке)
Кстати, может нам /инт уровня /матх запилить? Или им там всем будет похуй, как думаешь?
>инт
парень, который просил моар Что за инт?
Интернасьональ.
он нахуй никому не нужен
Мнение человека, который пять секунд назад узнал, что это такое, очень важно для нас.
Геометрия...
так и будет, проверяй
Спасибо, буду разбираться
Что?
Как доказывать, что копроизведение любых двух групп тривиально?
Тредик для наших друзей с загнивающего запада.
Оно не тривиально
Почему? Это ведь следует из существования гамалогии.
Гомологий не существует.
Доказательство?
Как отличить математика от маняматика?
Я их лично видел. Как это "не существует"?
А ты докажи, что существуют!
Умение доказывать аксиому выбора и существование гамалогий.
Ну это тривиально. Следует из универсального свойства когамалогий.
Можно ли доказать, что все гамалогии тривиальны?
Как доказывать, что абелевых групп не существует?
Есть семь разных предметов и куча коробок трех разных цветов. Количество всех возможных комбинаций коробок с предметами находится простым перемножением количества тех и других?
Находится простым применением аксиомы выбора очевидным образом.
Задача из теста на знание школьной математики:
https://meduza.io/quiz/pomnite-li-vy-shkolnuyu-programmu-po-matematike
Все остальное там несложно (на уровне арифметики и линейных уравнений), а вот здесь непонятно, откуда берутся 55 градусов?
https://meduza.io/quiz/pomnite-li-vy-shkolnuyu-programmu-po-matematike
Все остальное там несложно (на уровне арифметики и линейных уравнений), а вот здесь непонятно, откуда берутся 55 градусов?
Есть ли какая-нибудь доступная литература по теории категорий, лучше всего для школьников? Хочу писать на Haskell, а математику почти не знаю.
И нахуя тебе для него теория категорий?
Я монады не понимаю.
> Хочу писать на Haskell, а математику почти не знаю
А категории тут при чём?
И почему ты думаешь, что ты поймёшь их с точки зрения теории категорий?
Если есть желание и ты не совсем отбитый, то через недельку уже поймёшь.
Я открываю статьи/учебники по хаскелю, и натыкаюсь на кучу непонятных терминов, какие-то комбинаторы неподвижной точки, трансформаторы, эндофункторы, анаморфизмы, изоморфизмы...
Вот и хотелось бы наконец понять и разобраться, о чем идет речь.
У нас в вузе на факультете прикладной информатики ничего из этого не было.
Ну вот, например:
>Делаешь пандорический захват, лифтишь в монаду, потом строишь рекурсивную схему (здесь подойдёт зигохистоморфный препроморфизм) как монадический трансформер из категории эндофункторов, и метациклически вычисляешь результат. Любой второкурсник справится. А если делать на анафорических лямбдах — так задачка вообще на пять минут.
Не знаю, о каких второкурсниках идет о речь, о студентах Беркли? Мне знакомый препод не смог объяснить ничего в этой "задачке".
Не знаю теорию категории, но слова которые ты перечислил узнал из "Топосы. Категорный анализ". Также кто-то советовал "Теория категорий работающему математику"
Самое доступное что знаю - Category Theory, Steve Awodey. Наверняка что-то ещё более доступное есть.
Советую про теорию типов узнать, она тебе больше пригодится. Да и она очень сильно связана с теорией категорий.
>комбинаторы неподвижной точки
Это уже из лямбда-исчисления больше.
В любом нормальном учебнике объясняются термины, которые ты перечислил.
Есть Tom Leinster, "Basic category theory". Можно невозбранно найти на архиве.
С чего мы решили, что эти индуктивные множества то же самое, что натуральные числа? Они что обладают теми же свойствами или как?
Они являются моделью того, что мы интуитивно подразумеваем под натуральными числами.
Какой самый эффективный метод доказательства существования гамалогии?
Спросить у мамы
Что именно спросить?
Ручками показываешь, что существует одна гамалогия, потом показываешь, что для n гамалогий существует еще одна отличная от них. Доказываешь и применяешь аксиому индукции. Профит
Ну так гамалогия может и отрицательная быть. Тут уже аксиома индукции по целым числам нужна, а для этого нужна аксиома выбора насколько я помню.
Как доказывать существование гамалогии финитарными методами?
Как доказать, что любой цепной комплекс является точным?
>|x+4=x|
>|-2+4=-2|
>|2=-2|
Растановка модуля.
Ты не доказал, что натуральные числа существуют
Ну это совсем какая-то фигня. С делением на ноль лучше попробуй подобное.
О, N-петух. Натуральные числа существуют, поскольку являются конструктивным объектом и у них есть правила построения. И я тебе это сто раз писал.
А аксиома выбора существует? Возможно ли её доказать?
Как вообще доказывают существование гамалогии? Вообще никак не могу.
От обратного
Доказательство - это вычисление. У Воеводского в НоТТ это как раз открытая проблема, с аксиомой выбора доказательство есть, а вычислимого нету. Собственно, все что нужно знать о т.н. "неконструктивной математике" - заткнули дыры в вычислимости невычислимыми верованиями, типа "и так сойдет" и веруют, что проблемы нет, но все вылезает наружу при первой же попытке воспользоваться.
То есть мы можем определить для них все то же самое, что и для натуральных чисел? Сложение там со всеми свойствами и т.п.
Ты меня с кем-то перепутал. Я нюфаня в математике.
Если моя бабушка по папиной линии - украинка, то какая доля украинской крови во мне?
Если в роду остальных родственников никогда не было украинской крови, а бабушка состояла полностью из украинской крови, то ты минихряк: 25%
Копро-изведение это все посты ИТТ, начинающиеся с "как доказывать, что..."
Если ты кун, то у вас с ней нет общего набора хромосом. Разве что некоторые мутации могут общими.
так что примерно 0%
Если тян - сложно сказать.
Ну, да, типа того.
Что от меня хотят?
Посоветуйте сборник задач и упражнений по математическому анализу. Его кажется, еще какой-то Демидович создал.
Зачем тебе задачники по этой конченной хуйне?
Сегодня шёл домой с РАБоты и придумал задачу.
1. Коммутативность: ab=ba
2. Ассоциативность: (ab)c=a(bc)
(неверное)Предположение: если структура обладает коммутативностью, то она и ассоциативна.
abc=bac=bca
Найдите ошибку.
1. Коммутативность: ab=ba
2. Ассоциативность: (ab)c=a(bc)
(неверное)Предположение: если структура обладает коммутативностью, то она и ассоциативна.
abc=bac=bca
Найдите ошибку.
Опускать скобки можно только в ассоциативных структурах. В первом равенстве ты исходишь из предположения, что pqr значит (pq)r, во втором равенстве из предположения, что pqr значит p(qr).
>Предположение: если структура обладает коммутативностью, то она и ассоциативна.
На самом деле ты уже предположил, что она ассоциативна. Так что твоё доказательство тривиально верно.
Спасибо, аноны, посмотрю. А что из перечисленного из лямбда-исчисления?
В детстве читал по нему книжку какого-то советского профессора (Лаврова, кажется), но она была специально для школьников и начинающих программистов. Там лямбда-выражения приравнивались к анонимным функциям, которые могут быть параметрами других функций (высшего порядка), рассказывалось, как на языке Lisp запрограммировать операции над числами через 10 цифр и символы, как на нем моделировать бесконечную машину Тьюринга, ООП как в Smalltalk и т.д. Терминов практически не было.
Может быть какой угодно, в зависимости от доминантных/рецессивных генов. Считать такие проценты - глупость для расистов, даже евреи при въезде в Израиль их не вычисляют.
>А что из перечисленного из лямбда-исчисления?
Fixed point комбинаторы. Да и в принципе всё перечисленное сильно связано с лямбда-исчислением и теорией типов, так как они сильно связаны с теорией категорий.
Да, молодца.
Нет.
>Да
>Нет
У этих двух постов одинаковый смысл.
Доказать по индукции приведенные утверждения. Ассоциативность сложения и умножения, "дистрибутивность" модуля и т.п.
А трансиндукцией можно?
Intro2fp-ru.pdf наверни, например.
Тебе не надоело?
Что?
Как мне это тут использовать? Тут даже числа не натуральные
Используй трансфинитную индукцию, она и на вещественных работает.
Но от меня требуют, чтобы я доказал обычной индукцией. Я хочу сделать то, что требует от меня автор.
От тебя хотят, чтобы ты выбрал книжку попроще, если не можешь понять это. Хотя Зорич не требует никаких знаний, он предполагает, что ты хороший матшкольник, который уже знаком, например, с индукцией.
Обычная индукция эквивалента трансфинитной индукции если у тебя аксиома выбора верна.
Тогда может мне следует подтянуть какие-то темы из школьной математики? Прочитать пикрелейтед? Это поможет?
Первой не хватит, но пролистай ее. Она не сложная. Вторую сейчас посмотрел, по-моему слишком специализированная. Сложно и узко. Я бы на твоем месте, если ты нулевой, потратил месяц на школьные олимпиады (без геомы). Зорич после этого не пойдет как по маслу, но у тебя будет хороший кругозор. Попробуй "ленинградские математические кружки". А дальше сам смотри, чего не хватает
> ты нулевой
Не нулевой, в школе вроде проблем с математикой не было, все легко понимал. Но школа у нас была хуевая, поэтому учили очень ограниченно.
Ладно, спасибо за помощь. Поступлю как ты сказал.
>в школе вроде проблем с математикой не было, все легко понимал
Это далеко не показатель. Я вот в школе ничего не понимал.
Если ты впервые сталкиваешься с заданием 7-8 класса на индукцию, то я смело назову тебя нулевым. Конечно, по меркам матшкольника, а не птушников
>матшкольника
Что такое "матшкольник"?
С гомологиями понятно. Понимаешь как существование 2Z доказать?
Что с ними понятно? Подскажи, может ли 2Z быть гамалогией? Существование пусть будет аксиомой.
y''+ (a^2)y = tg(x)
При каких а существует единственное непродолжаемое решение с областью определения (-1;3/2).
Я так понимаю, что раз все функции на этом промежутке непрерывны => мы можем поставить сколько угодно задач Коши и каждая будет решаться. И ответ ни при каких. Мне кажется слишком простое решение, чтобы быть правдой.
При каких а существует единственное непродолжаемое решение с областью определения (-1;3/2).
Я так понимаю, что раз все функции на этом промежутке непрерывны => мы можем поставить сколько угодно задач Коши и каждая будет решаться. И ответ ни при каких. Мне кажется слишком простое решение, чтобы быть правдой.
Серьёзно, подскажите может ли 2ℤ являться гамалогией?
За что мой пост удаляют? Подскажите может ли 2ℤ являться гамалогией?
Не могу понимать очень многие алгоритмы, немного сложнее, чем пузырьковая сортировка, из-за того, что математику успешно проебал в школе, как и все предметы, вообщем-то.
Может кто посоветовать книжки по развитию алгоритмическому мышлению(понятное дело, что развивать очень хорошо можно, если ты решаешь задачи, но тут тоже нужно знание математики) и еще, если можно учебники по физики.
Ну и что бы доказать, что я не ленивое хуйло, я действительно искал такие учебники.
По математики я нашёл учебник Сканави. Но он мне показался слишком сухим, а по физики - Фейнмановские лекции, но тут объясняется для тех, кто уже что-то понимает в физики, может есть что попроще?
физике*
Каких форсов? Ты в каком-то чатике ещё сидишь? Извини, такой хуйнёй не страдаю и не понимаю.
Math, хочу с энтри левела разобраться в том что такое мат. индукция и научиться доказывать различные вещи с ее помощью. Посоветуй, что почитать на тему.
Советую почитать Генцена и Гёделя. Я думаю лучше них в этом деле пока ещё никого не было, да и пишут довольно доступно для начинающего.
А конкретно в каких книгах про индукцию и доказательство?
Считаю вот это самым лучшым для твоих целей:
Генцен - "A treatise on transfinite induction and its applications".
Гёдель - "On the inductive nature of proofs of the axiom of choice".
В каком смысле? Я действительно посоветовал то, что считаю хорошим.
Ты поехавший абсолютно
А мне никто не поможет? Или слишком избитый вопрос, что бы на него отвечать?
Не он, но вроде тут хороший совет
Переводы на русский должны быть тоже.
Читай школьные учебники
Параллельные линии это тоже в некотором роде абстракция (мол идеально не сделаешь в реальной жизни) или у меня что-то с восприятием?
Для нулевых самое то. Если быстро пробежаться по этому материалу, то он не усвоится и останется тебе только быть клоуном как
Через лет 500 спроси, когда мы уже наконец узнаем больше о нашем реальном мире.
>Для нулевых самое то.
Ааа, я вижу тебе это очень знакомо. Ну хорошо, в таком случае не буду спорить.
В реальной жизни и линий нет
Ну вы меня и запутали. Просто когда я смотрю на параллельные линии, мне они кажутся совсем чуточку не параллельными. Но вроде же можно как-то перенести на координатную плоскость и тогда понять. Креститься надо?
Где ты на них смотришь? Линии должны быть бесконечными в обе стороны. У тебя такие?
Я бы ответил, но боюсь, что ты и есть он. Не хочу кормить тролля. Просто почитай тред и сам поймёшь.
Спасибо, но я не могу найти ни одной из этих книг. Осмелюсь предположить, что это не названия книг, а что-то другое, типа названий глав в книгах?
Так я и почитал, все равно не совсем понимаю, о чём ты.
Список книг в виде пополняемого репозитория:
https://github.com/uburuntu/mm_books
https://github.com/uburuntu/mm_books
>Книжная годнота для математиков
Но я не математик((0(
>ленинградские математические кружки
Решаю задачи нулевого цикла и возникают проблемы с их решением. Я совсем тупой и мне стоит забить на математику или они не должны легко решаться?
Для тех, кто раньше не занимался математикой, не должны. Там почти везде (кроме нулевого цикла) есть решения, так что разберешься
Поясните за книгу Куранта "Что такое математика". Что оно должна дать? Что там рассказывается? Есть от нее польза? Что думаете о ней?
>“Математический анализ в 57 школе“
Но это разве не методичка для учителя, а не учебник?
Но это разве не методичка для учителя, а не учебник?
Они эти задачки с преподом разбирали 1 на 1. Для соло обучения вещь сомнительная.
Бамп вопросу.
Соло тяжко и больше риск выдохнуться без поддержки, забредя в очередной тупик. Ну если ты родился более-менее математически одаренным и не с двузначным IQ, тогда может и легко будет в одиночку поглощать сложные книги.
Понятия не имею, но под "двузначным IQ" я имел в виду заметную туповатость, которую прозреваю у себя.
>Понятия не имею
Для начала бы и просто представления, были бы неплохи.
Я знаю, что тут есть погромисты. Озвучьте список дисциплин, которые вы считаете необходимыми к изучению для всякого уважающего себя погромиста, пожалуйста. Мне на ум приходит только дискретная математика: множества, графы, матрицы, комбинаторика, алгоритмы, булева алгебра, предикатная логика, вот это вот всё.
Обычному программисту достаточно арифметики, начал алгебры, и немного комбинаторики.
Её хоть кто-то открывал? Основные темы там не такие уж экстраординарные, самое интересное в доп. листках.
Шень. Начала теории множеств.
Еще бамп вопросу.
Бампаю под сагой, это я молодец.
Но ведь это сильно зависит от области работы. Один драйвера пишет для железяк, другой machine learning мутит, третий игры делает, четвёртый сайты за доширак.
Посоны, ебусь уже сутки, но не могу найти решения, даже придумать его не могу, не понимаю, что требуется. Может кто даст советов мудрых?
Вес теста 115кг с влажностью в 24% Сколько нужно добавить в тесто муки с вл-тью 13%, чтобы получить в итоге тесто с влажностью в 22%
Решения не прошу, но наводящий вопрос или совет, очень бы помог.
Если я буду добавлять муку, то как блядь уменьшится влажность, если она будет увеличиваться?
Она будет уменьшаться, потому что проценты выражают пропорциональное отношение. Если в кучу влажной хуйни добавить кучу менее влажной хуйни, то en masse получится менее влажная хуйня.
Пусть x - масса сухой муки, y - масса воды. Тогда масса теста есть z = x+y, ибо тесто состоит из воды и муки.
Влажность определим как y/z. Если масса теста 115 кг и влажность теста 24%, то в этом тесте 27.6 кг воды.
Аналогично определим влажность влажной муки. Её добавим мы x килограммов.
Тебе требуется найти такое x, что (0.13x + 27.6)/(115+x) = 0.22.
Это очень хороший ответ. Спасибо анон, добра тебе. Пойду решать, теперь стало понятнее.
Посоны, не могу придумать тему для курсача.
Хочу чего-нибудь не слишком сложного, но чтобы можно было рисовать красивые дохуямерные графики и вот это всё.
Объём небольшой, так что здоровенные темы не предлагать.
Хочу чего-нибудь не слишком сложного, но чтобы можно было рисовать красивые дохуямерные графики и вот это всё.
Объём небольшой, так что здоровенные темы не предлагать.
Рассчёт ящика
xddddd
ЧТо скажите про Конкретную математику?
Я тут уже несколько дней мучаюсь. Подскажите пожалуйста, может ли группа 2ℤ является гамалогией?
Ничего, послезавтра пойдешь в школу и там тебе объяснят
Теперь там
> Книжная годнота по математике
:|
Завтра в школу, а я ничего кроме мемов /math не выучил. Что делать?
Мемить гомологии и аксиому выбора, чтобы потралевать училку
И снова бамп ОДУ.
Если задашь адекватный вопрос, то получишь адекватный ответ. Или нет. Зависит от степени лени местных. Чужие домашки они делать не любят, а спорить об основаниях любят.
Задать его.
Раньше у вас здесь вроде бы FAQ был, но сейчас хз че. Короче хотел бы узнать с какой книги начинать изучение математики, вот допустим я человек который умеет только цифры складывать простейшими операциями и корень из числа вычислять, на этом всё. Вроде бы когда-то давно советовали эту книгу - http://www.ozon.ru/context/detail/id/139124756/ , хотелось бы получить отзыв от сторожил данного треда. С чего всё таки начать?
Сначала тогда изучи арифметику и геометрию. Ну, а алгебра потом.
>сторожил данного треда
И с чего ты взял что этот совет будет хорошим?
Это был неадекватный вопрос. Вот тебе экспертное заключение. Всё просто.
Вычислять без калькулятора корень из числа геморройно. Значит, ты уже много знаешь.
Ну мне бы именно литературу. Грубо говоря с какой книжки начать?
А чем неадекватный вопрос отличается от адекватного?
Алгебра 7 класс. Можешь начать с Гельфанда/Шеня, но там задачки сложнее, есть вероятность застрять и расплакаться.
Киселев "Арифметика".
Неужели мой вопрос неадекватен?
Просто в нём нет гамалогий.Тут никто не умеет решать такое
логл матановая капча
Я помню тут было много парней, которые шарили в ОДУ. Да и раз тут постоянный срач между матанщиками и гамологами(или кто там с кем срется, но я точно помню, что здесь куча адептов Арнольда) то в чем проблема решить подобное? Или я не в том треде пишу?
Спасибо, Гельфанд у меня был как раз и в прошлый раз мне его советовали. Надеюсь освоить за неделю, реально ли? (там вроде 200 страничек). Имею 6-7 часов свободного времени в день.
Попробуй, расскажешь через неделю.
Фак же в шапке по ссылке.
Ну так это реально или же нет?
Есть же специальный тред https://2ch.hk/math/res/21605.html
Больше некуда, пиши туда.
Книга Гельфанда какая-то странная, написано что она покрывает материал до 9го класса, и при этом там всего 140 страниц учитывая предисловие и тексты задач. Там вообще хоть что-то объясняется или это не учебник а некий справочник?
Объясняется. Видно же, что в начале даже учат яблоки считать. Школьную программу за 9 классов полностью точно не покрывает.
Я просто искал какой-нибудь учебник который полностью покроет 9 классов, чтобы можно было за месяц примерно вспомнить весь материал и дальше уже заниматься чем-то другим.
>то в чем проблема решить подобное?
Я хз как решить, другие тоже, наверное, раз молчат.
Нихуя.
Мимонаходил корни из трехзначных чисел на школьных контрольных на бумажке.
Это не совсем самодостаточный учебник. а дополнительное учебное пособие с обилием задачек, чтобы освежить и подкрепить основную программу, которую должны дать в школе. Неужели это не очевидно?
Дорофеев-Потапов-Розов покрывает за 11. Аленицын-Бутиков-Кондраттев тоже, только он еще и всю школьную физику заодно.
Начни с Гашкова.
>P. Grillet: "Abstract algebra". Очень лаконичный и понятный учебник. Надо знать элементарную теорию чисел, про индукцию, про множества и функции. >Линейной алгебры нету
Бля, да вы охуели, дети. Зачем составлять фак, если ты не понимаешь материала? Есть там линейная алгебра, разуй глаза, блядь. Более того, не существует graduate textbooks по алгебре, где бы не было линейной алгебры. От слова вообще.
Напоминаю специалистам, что линейная алгебра бывает разной. Если вы видите в названии слово "конечномерный", eg: Конечномерный анализ, конечномерные алгеры и тд – как это ни странно, перед вами книга по линейной алгебре. Рекомендую посмотреть определение Банахова пространства. Если же книга называется "алгебра", но вот про матрицы и векторные пространства там что-то ничего не написано: не отчаивайтесь и открывайте главу про свободные модули. Она там есть, точно.
Ну я вроде и спрашивал об этом. Есть ли какой-то учебник который затрагивает 6-9 класс по которому можно заниматься? Или стоит просто качать учебники для каждого класса по отдельности и заниматься по ним?
Если сначала начну с - М. И. Сканави: "Элементарная математика". А потом продолжу - С. Б. Гашков: “Современная элементарная алгебра” , то не будет ли повторения материала? Стоит ли именно так двигаться?
дополнение к этому посту:
На первый взгляд (судя по оглавлению) кажется что эта книга затрагивает как раз весь период с 5 до 9 класса, так ли это? Качество скана правда хуевенькое =(
фикс: эта книга - М. И. Сканави: "Элементарная математика"
Сканави нужен для наработки техники. Полезно, но не про понимание. Мне и другим сложно ответить потому, что школьную программу мы как то неосознанно ответили. Поэтому просто читай все, что можешь и решай все, что вызывает трудности. Все равно, когда вырастешь, навык перебирать и искать книги понадобится.
то школьную программу мы как то неосознанно освоили.
починил
Не понимаю доказательство теоремы Гудстейна:
ну окей, сопоставили каждый элемент последовательности ординальному числу.
И эти ординальные числа уменьшаются с каждым шагом.
Почему можно утверждать, чточисло за конечное число шагов станет равно нулю.
Ординалы-то мы рассматриваем не только конечные, но и счётные.
p.s. аналогичный вопрос про теорему о гидре
Короче я уже попробовал почитать начало каждой книги про которую написано в FAQ из раздела элементарной математики или арифметики - и там все книги рассчитаны на тех людей кто уже знакомы с математикой для студентов короче. С первых же страниц начинается разбор каких-то дробных выражений, везде корни, ещё фигня какая-то и тд. Похоже правда придется просто качать отдельно учебники по математике для каждого класса от 5 до 9го и учить именно так.
Тебя уже тыкнули носом в элементарные учебники Киселева. По конкретным темам можно покопаться в школьных книжках на сайте МЦНМО.
Научись уже сам искать книжки по потребностям. Интернет утопает в вопросах, подобных твоему, надо просто немножечко пошарить.
Если ты нулевой и не хочешь утонуть во множестве лишних(пока) деталей - тебе к Киселеву. Книжка Сканави не является нормальным учебником, это видно в частности по оглавлению.
Не ругайся кисик, не видишь разве какой я глупый? А есть какая-нибудь существенная разница между изданиями Арифметики Киселева 2002 и 2017 года? Или всё равно, просто новое издание вроде не выложили ещё.
У меня дежа вю, или этот же вопрос задавали тут пару месяцев назад?
Главное - не бери книжки от URSS. Никогда.
Этому факу лет больше, чем тебе
Суп, выручайте
Нужен алгоритм для нумерации всех возможных по целых чисел
Нужен алгоритм для нумерации всех возможных по целых чисел
*пар целых чисел
Быстрофикс
Идея вот.
Бл, подумал, что натуральные, вот для целых (формулу накатать еще можно):
Почему в подобных факах я никогда не видел Туманова? Хороший же учебник.
16 задача. Помогите, у меня получается какая-то залупа сложная непонятная. в Гугле страница с решением и сохранённая копия не открываются
Бля
В процессе решения возникла ещё вот такая проблема. В чем подвох?
Идея-то есть. Проблемы возникают именно с формулой
Бля решил
#40. Не смог решить ни один пример, позвонил деду, он сказал нужно в числителе и знаменателе вынести множитель, чтобы сократить. Продолжал так делать до д, дальше нихуя не понимаю, что там можно вынести за скобки, чтобы сократить. Не хочу заёбывать деда, помоги, двач.
В этих заданиях суть разложить на множители, в д в знаменателе выносишь 3, в числителе раскладываешь разность квадратов, из 5 - а выносишь -1
Так?
Мне просто интересно, откуда ты взял y.
Ты про написание?
Завали ебало, модульный дед.
>Сканави
>для самых маленьких
Да это вообще пиздец, какие-то шизофреники этот фак писали, они бы ещё Бурбаки сказали читать. Забей на это большой хуй и лучше действительно читай школьные учебники, можешь ещё по ютубу порыскать, там много видео по математике.
Сканави - это пособие для учеников седьмого класса и выше вообще-то.
э ты че обзываешься?
Ну вот Киселева открыл, там достаточно подробно всё, даже очень. Пока Аримфетику читаю, решил дроби повспоминать.
Слишком строго написано, тяжело читать.
Скорее нет. Это для студентов, которые хотят освежить знания и чем-то дополнить их. Так даже в самом оглавлении написано.
Ну так что, матач?
Слились?
Вроде что-то похожее на формулы было выше. Ты знаешь как нумеровать целые числа?
Потому что это не учебник.
Разница есть только между дореволюционным Киселевым и переработанным совками. В предисловии к совковому изданию написано, что изменено.
>модульный дед
Что это такое?
Есть издание только 2002 года, более новое к сожалению не нашел.
По какому принципу нумеровать отдельные целые – да, парочки целых – да, а вот формулу – нет
Только первое издание Грийе вышло в 2006, когда я уже школу закончил. То что я раньше не заглядывал в фак, его никак не опрадывает.
Это все репринты, а не новые издания. Искать смысла никакого.
Хочу вкатиться в machine learning. Неплохо знаю Python, но с математикой никак. Нужны матрицы, вектора, пределы, производные, интегралы, всякое такое. Ну и теория вероятностей. Знаний об этом у меня ноль. Как можно в это вкатиться ньюфагу? Mathprofi?
Советую начинать с гамалогии.
Разве, вроде в каждом издании должны быть какие-либо переработки, тем более когда обложку меняют. Если не меняют - значит репринт просто. Там вроде даже количество страниц другое, значит в любом случае какой-то редизайн (хоть и незначительный) был.
Конечно разницы нет, но просто интересно что там изменили.
Что такое point-slope form? В словарях нахожу перевод как "уравнение пучка прямых с центром в точке", хотя вариант английский выглядит как-то попроще, школьный уровень возможно даже. Не понимаю зачем эту формулу применяют и что получают в конце.
>Как можно в это вкатиться ньюфагу?
Precalculus.
Calculus, linear algebra.
Measure theory.
Probability theory.
Вот по порядочку описанные тобой темы. Книжек и прочего полно в гайдах из шапки. Вообще это всё уровень матшкольника, но у нас в деревнях перечисленное изучают на первом курсе универа, за исключением теорвера.
Одна из форм линейного уравнения. Позволяет задать линию имея координаты одной из её точек и слоп(угловой коэффициент).
Как?
Ну и нахуй он усрался? К олимпиадам готовиться? Ах ты мразь ебанутая, иди свой интеграл считай, скотина больная.
Ты чё несёшь, анимешник больной?
Это такой школьный юмор в этом году в моде? Внимательно: в числителе разложи на множители.
Посоветуйте литературу по теме, и чтобы было не слишком сложно. В универе этот раздел не проходили.
Ты в универе должен был изучать матан(калькулюс и даже свыше него) и линейку на первом курсе. Гуманитарий что ли?
Спасибо! Буду разбираться.
Не знаю насчёт него, но я тот самый анон, который задавал вопрос про ML и я гуманитарий, да. Профильную математику на ЕГЭ сдал на 60 баллов.
Анон, какой раздел посоветуешь основательно изучать первым? Пробовал и матан, и теорию множеств/логику, и абстрактную алгебру, и топологию, везде нахватался верхов, по сути ничего и не знаю. Есть ли раздел, с которого однозначно стоит начинать и почему это матан?
Тупой вопрос, но всё же. Всем известно, что ∞ + 1, ∞ × 2 и т. д. это всё та же бесконечность, мощность множества остаётся прежней, между двумя элементами множеств можно найти биекцию и всё такое.
И всё же, если у нас есть бесконечная последовательность вида: ♥✗✗♥✗✗♥✗✗♥✗✗♥✗✗…, то ✗ в ней будет в некотором смысле больше (причём ровно вдвое больше), чем ♥. Есть ли способ это как-то формализовать?
И всё же, если у нас есть бесконечная последовательность вида: ♥✗✗♥✗✗♥✗✗♥✗✗♥✗✗…, то ✗ в ней будет в некотором смысле больше (причём ровно вдвое больше), чем ♥. Есть ли способ это как-то формализовать?
Напиши описание к нему, добавим.
Шутка, бро, не кипятись. Лучше накинь ещё правок.
Ознакомься с учебными программами по математике, рекомендациями профессоров. Не забивай на учёбу в своём вузе. Матан отнюдь не краеугольный камень всего, хотя то же дифференциальное и интегральное исчисление применяется относительно широко.
Я лишь стараюсь подсказать что-нибудь таким же, как сам, поскольку больше в этом разделе делать нефиг. Какие-то проблемы?
Ты сдал ЕГЭ лучше, чем я. Поздравляю.
Книги в шапке. Всё в шапке, даже небо. Читайте йоба-гайд с форчана https://sites.google.com/site/scienceandmathguide/subjects/mathematics там гора всяких интересностей.
Смысл жизни и есть в обладании этим смыслом.
Об этом мы не имеем права даже молчать.
Об этом мы не имеем права даже молчать.
Вас тоже уже з@εб@л конструктивисто-дебил? У него в голове кроме говнавычислимости нихуяшечки же нет.
Хорен, похоже, набухался. В честь чего только, интересно!
Думаю, что Хорен как раз тот человек, который сможет оценить комплекс идей Новой парадигмы мировоззрения с Критерием истины.
Несколько цитат:
Квантовый Мир один, целостен, логичен, а все мы его неотъемлемые части. Откуда немедленно следует Критерий истины.
Вера есть яркая визуализация достижимой цели, иначе это фантазия.
Самое простое определение бога - Бог есть самая сложная сущность Мира.
Бог автоматически появляется на VII этапе развития цивилизации по шкале Кардашёва.
Каждый может мнить себя правым, но прав лишь Единственный Бог, который обладает максимально возможными ресурсами и самыми полными Базами Данных знаний для выработки взвешенного решения.
Ответ на коан "Кто я?" Я есть квантовая пустота, искажаемая рябью суеты на планете Земля.
Любая планетарно-звездная цивилизация погибнет или будет существовать вечно. Это истина в 1 бит.
Новая парадигма мировоззрения необходима любой звездно-планетарной цивилизации для успешного прохождения Технологической сингулярности.
https://youtube.com/watch?v=LrgCGtMFeyU
Вы знаетее, ассоцаасации все, все берут меня в клешни.
Всемм известно, что что в английсксйком l" на конце (двойная: shall, ball) читается как "темная". Ммоя ассоцтация с этим звуком: венозная коорвь.
Вы знаетее, ассоцаасации все, все берут меня в клешни.
Всемм известно, что что в английсксйком l" на конце (двойная: shall, ball) читается как "темная". Ммоя ассоцтация с этим звуком: венозная коорвь.
>>>24230
>Новая парадигма мировоззрения
Витгенштейгн и его трансцндентное.
>Новая парадигма мировоззрения
Витгенштейгн и его трансцндентное.
Матач, что происходит на http://www.mi.ras.ru/?c=noc? Где расписание на новый семестр? Они будут работать в этом семестре? Может быть, они уже начали, но простым смертным не сообщили? Кто-нибудь знает?
я подскажу как это сделать для пар состоящих только из положительных, для всех остальных тебе понадобится по сути запихать 4 пары вместо одного, в этом тебе поможет умножение на 4.
А для целых смотри.
(1,1)(1,2)(2,1) ...(n, m), и вот если у нас м н, то на каком месте он будет стоять? Как это зависит от н и от м? н - это столбец, а м - строка, ну или наоборот, неважно.
> Самое простое определение бога - Бог есть самая сложная сущность Мира.
Бог есть самая существенная и необходимая структура бытия! Иными словами, самая общая и необходимая истина, закономерность, без которой невозможно существование чего-либо.
Самое простое определение Бога — Бог это всё.
Оно же и наиболее верное, потому что наименее засорённое конструктами человеческого мышления (если думать о мышлении, как о конструировании моделей, потому как модели по своей сути являются костылями, необходимыми человеку для осмысления реальности, ввиду принципиальной неспособности человека воспринимать и осмысливать реальность непосредственно).
Ну, я так считаю.
Наименее засоренное конструктами, в том числе материальными, – это определение Бога через Логос.
> если думать о мышлении, как о конструировании моделей
Дело не в самих моделях, а в том, что мы описываем ими. Хоть их и не существует, закономерность все же есть. Бог же является самой необходимой и важной истиной и закономерностью вообще, а также первопричиной не только относительно мира явлений.
Для этого тебе сначала придётся определить Логос. Что, как мне кажется, тоже чересчур сложный и надуманный (как это вообще свойственно грекам ≈500 л.д.р.х) конструкт.
В то время "всё" достаточно простая и интуитивная вещь. Не потому, что это слово реально является определением Бога, а потому что оно представляет из себя как бы "автоматический механизм", продолжающий "определять" Бога после того, как разговор окончен. После того, как было сказано, что Бог есть всё, "учитель" удаляется, а "ученик" может сколько угодно продолжать постигать Бога через ряд вопросов типа "вот эта кружка — Бог?" (да), "мой кот — Бог?" (да), "материя это Бог?" (да), "мои мысли — Бог?" (да), "мои чувства — Бог?" (да), "число — Бог?" (да), "изоморфизм между (ℝ, +) и (ℝ⁺, ×) — Бог?" (да) и т.д.
> Дело не в самих моделях, а в том, что мы описываем ими. Хоть их и не существует, закономерность все же есть.
Нет, не так. Закономерность — продукт человеческого мышления. Человек просто вынужден искать закономерности и объяснения, потому что иначе он неспособен воспринимать реальность. То есть, человек в принципе может после некоторой рефлексии понять и принять мысль, что "реальность (в прошлом, настоящем и будущем) — она просто есть", но это не даёт ему реального, непосредственного знания, ощущения — что же там "было, есть и будет". Некоторые буддисты-адвайта-ведданты и т.п. любят говорить о своём чувстве единства со Вселенной, но на деле человеку обычно приходится построить астрофизику, чтоб получить (очень неполное, несовершенное, но хоть какое-то) представление о далёких звёздах или придумать хотя бы Ньютоновскую механику и провести расчёты, чтоб хотя бы примерно предсказать, как скоро упадёт на землю брошенный кем-то мяч.
Человеческие мысли это как бы "сжатие с потерей", необходимое, потому что сжимаемый материал слишком велик, чтоб уместиться на носителе полностью и, тем более, чтоб производить с ним (исходным материалом) какие-то операции непосредственно.
Ты как-то плохо начинал, значит. Но главное не то как начнёшь, а как закончишь, правда ведь.
Начинай с теории множеств, а затем алгебру. Основы логики и так, в принципе, достаточно тривиальны, но серьёзно за неё браться на этапе становления не следует. А! Вот еще что: научись методам доказательств, да и вообще воспитывай в себе привычку всё доказывать. Матаном потом успеешь заняться, тем более, что как этот анимешник сказал, он широко применяется, и тебе просто в прикладных целях будет очень полезным и нужным его знать.
Где найти людей которые хотят подтянуть школьную математику и дальше?
Одна из самых популярных здесь тем
Вычти почленно ряд сердечко-крестик-нолик.
Непрерывно ли множество неалгебраических чисел? И если да, то как это вяжется с фактом, что алгебраические повсюду между них?
Зачем тебе люди? По учебным материалам, которые часто здесь упоминали, можно спокойно заниматься самостоятельно, там нет заданий с "подводными камнями".
Да я вот как-то не слишком спокойно занимаюсь...
>Не забивай на учёбу в своём вузе
Учусь не на математика вообще, в том и дело что математика это хобби, уделять ей столько же времени, сколько есть у студентов, учащихся на матфаке, не получится.
>Начинай с теории множеств
Наивной хватит, или упарываться аксиоматическими теориями?
> алгебру
В какой момент можно будет переходить с алгебры на другой раздел? Алсо почему именно алгебру советуешь?
=> /psy
А есть где списочек разделов и теорий, необходимых к изучению для понимания доказательства ВТФ? Ну или как на буржуйском запрос сформулировать? гуглтранслят не особо помог
> Алсо почему именно алгебру советуешь?
Математика царица наук. Алгебра царица математики.
Добрый вечер, Господа!
Есть Один Предел: lim(n->oo)(((n!)^(1/n))/n)
Интернет говорит, что ответ здесь 1/е, но решения не даёт. Сам решить не смог.
Желательно не использовать правило Лопиталя, и вообще решить как можно проще. Но рад буду любому решению, и даже совету, кроме совета идти в школу.
Есть Один Предел: lim(n->oo)(((n!)^(1/n))/n)
Интернет говорит, что ответ здесь 1/е, но решения не даёт. Сам решить не смог.
Желательно не использовать правило Лопиталя, и вообще решить как можно проще. Но рад буду любому решению, и даже совету, кроме совета идти в школу.
> В то время "всё" достаточно простая и интуитивная вещь.
В то время это противоречиво.
> Нет, не так. Закономерность — продукт человеческого мышления.
Все так. Образ закономерности в голове не есть сама закономерность, но есть ее образ. Кружка или кот перед тобой есть и существует по некоторым законам. Самое общее и объективно существующее – это нетварные законы, то бишь Логос.
> Человеческие мысли это как бы "сжатие с потерей".
Вот. Истинное утверждение не есть сама истина. Альфред Тарский определяет эти понятия таким образом: высказывание “Q есть P” истинно тогда, когда Q есть P. Например, высказывание “Земля имеет эллипсоидную форму” истинно, если Земля действительно является эллипсоидноподобным телом. Таким образом, истинность и ложность выступают характеристикой наших мыслей и высказываний о реальности или не реальности. Но сама реальность никуда не денется, как и закономерности, присущие ей.
Противоречивость — такой же выдуманный человеком концепт. С точки зрения Бога его не существует. Ему не нужно объяснять кому-то, что он такое есть, поэтому возникновение противоречий — проблема объясняющего (в данном случае — тебя) самому себе "что же это такое".
Заметь, что я не говорю о том, что это определение в рамках каких-то концептуальных систем — не является противоречивым (хотя это так). Это не важно. Важно то, что концепт противоречивости — шлак, грязь, выхлоп человеческого мозга.
Разумеется любые слова и идеи — такой же выхлоп. "Всё" в этом смысле удобно лишь потому, что оно простое и таким образом может привести к относительному просветлению коротким путём. А может и не привести, конечно, это зависит уже от гибкости ума.
А вот "Логос" — точно ни к чему не приведёт. Идея Логоса была нужна только когда человеческая культура была достаточно материалистична и непосредственна, чтоб пифагорейская философия и платонические идеалы могли бы предоставить, так сказать, "альтернативный взгляд". Для современного человека, который живёт с ощущением, словно бы математика в самом деле существует сама по себе — это только вредно.
> Все так.
Ты, конечно, можешь думать как угодно, я излагаю свою позицию. Она в том, что — ещё раз — нет, не так, всё это полная хуйня. Все эти слова, мысли, идеи, концепции — это порождение человеческого мышления. Закономерности не существует, это то, что многим так трудно понять. Это сказка, которую люди рассказывают сами себе, потому что так думать — приятно. Потому что чтоб понять, что набор частиц находящийся перед тобой в точке пространства-времени, которую ты называешь "будущим" начинает мяукать — тебе нужно упростить картину, назвав этот набор частиц "котом", который мяукает, когда хочет жрать. Ты находишь какой-то паттерн в поступающих тебе данных, который по твоему опыту всегда выполняется и назваешь его закономерностью. Это выглядит чудесно, словно всё действительно так и есть, словно F = am и всё такое. Но все эти "F = am" ты ну не лично ты, но это детали сам придумал, потому что они наиболее близко описали известную тебе реальность.
Человек — такой механизм, которому необходимо выдумывать закономерности, иначе он не может функционировать. Они возникают в мозгу у человека где-то на пути между поступлением сигнала в его органы чувств и движением его тела в направлении жратвы. А все "треугольники", "числа", "атомы", "логосы", Витгенштайны, Ньютоны, многочисленные алгебры и геометрии и прочая словесная мастурбация — это всё просто побочный продукт.
В реальности же — т.е., с точки зрения Бога — нет ни кота, ни корма, ни звуков, ни массы, ни ускорения. Ни субъектов и объектов.
Поэтому, да, логос — это Бог. И воздух, которым ты дышишь — Бог. И ты сам — Бог. И всех вас не существует вне твоего мозга. И в твоём мозгу, на самом деле, тоже — там только клетки и электрические импульсы.
Уебывайте в отдельный тред со своей философией.
Не понял тебя.
https://mathoverflow.net/questions/97820/a-recommended-roadmap-to-fermats-last-theorem
Не то скопировал, извини.
С наивной лучше.
Я опирался на его слова о том, что математика для него это хобби.
Не значит.
Как геометрически изображается диагональ цилиндрической поверхности? "обвивающая" линия?
Если f(x) = 0,5x, то f(2x) = x?
Если это так, то тогда как это доказать?
Если это так, то тогда как это доказать?
f(2x) = 0,5(2x) = 1x
мимио-перельман
2x=t => f(2x)=f(t)=0.5t=0.5*2x=x.
По сути функция делит аргумент на 2, новую переменную она так же будет делить на 2.
Тогда, если sin(2x) = 2sin(x)cos(x).
Видно, что в формуле аргумент понижается в 2 раза.
3x = t => sin(3x) = sin(t) = 2sin(t)cos(t) = 2sin(1.5x)cos(1.5x).
Я прав или лучше по-другому оформить?
это из книги?
Проверил через формулу Эйлера, вроде все так. Но вообще, не стоит путать линейные функции, коей является первая, и нелинейные. Это
> sin(2x) = 2sin(x)cos(x)
по сути функция вида f(c*x)=g(f(x)).
Нет. Нашёл старые записи из 10-ого класса по теме пределы, давали доп. заданием. Так и не смог тогда решить, а вот теперь интересно же, как его грамотно доказать.
Ответ взят из интернета, однако, в записях так же фигурирует, как правильный - подсказка учителя.
И какая вообще разница, откуда пример?
Как доказать, что когамалогия существует и к тому же является уникальной?
Попробуй доказать, что ((x!)^(1/x))/x = ((x-1)/x)^x. Если получится, то предел последнего является следствием из второго замечательного предела и равен 1/e.
Загугли формулу стирлинга и реши, тебе в другом треде ведь уже написали
Ненавижу математиков, может встретимся? Я вас всех разъебашу ,черти.
C]t,fk d cdjq gjgjcnfy? vhfpm
А теперь по нормальному.
Почему формула ньютона-лейбница работает?
Я понял суть. Ищем мы площадь под кривой, берем два бесконечно близких значения функции, умножаем на любое число между ними. Смотрим на результат и говорим "Так так так......ЕБАААААТЬ да ведь это же похоже на дифференциал функции. А давайте как найдем эту самую первообразную функцию от сих до сих и сравним ответы с нашим суммированием."
Я спрашиваю почему она работает не только на бесконечно малых интервалах? Или тут, неявно, тупо суммируют бесконечно малые по абсолютному значению первообразные,
Ее разве проходят в школе? Анону нужно решение уровня 10 класса.
В общеобразовательных школах пределы вообще не проходят. В моей не было, во всяком случае
Производные и интегралы проходят, значит и пределы проходят, по крайней мере у меня было так.
По какой теме?
производные и интегралы проходят чисто "табличкой". Типо есть такие функции, выучите их производные. Не о каких приращениях там не говорят.
Хуй знает, что ты учил и когда, то ли слишком давно, то ли совсем недавно. Сам закончил обычную школу 6 лет назад, учил и приращения, и пределы, производные детально проходились, интегралы менее детально, но все же не на уровне просто табличных. Ну да ладно.
Посоветуйте сборник тождеств по математике. Можно по тч, комбе.
Доска не о том, но как все-таки плавно заехать в физику? Студент 1 курс, по физике пиздец какой-то, интегралы/пределы и задачи с этими йобами. Мб есть книжка годная, где вначале теория желательно с ВЫШМатом и тд, а потом практика
В любом учебнике матана есть доказательство
Думаю, это тебе поможет http://ilib.mccme.ru/djvu/zeld-yag.djvu
начали учить матрицы. чувство, что задание легчайшее, но не понимаю, что дальше делать-то? формулы для определителя знаю, но какие тут элементы...
Как доказать, что каждое дискретное пространство имеет тривиальную первую когамологию?
Ищи определение A_{i}
нужно построить график. получается чушь( помогите пжл
Бамп из последних сил.
А что за хитрые вычисления? Почему тетрадь в линию, грязь кругом? Ты не уважаешь древнейшую науку?
Ну можно просто по-дедовски составить таблицу и сделать график, а дальше я не знаю, тут какая-то хитрая матеша наверное есть, чтобы типа найти самое большое по абсолютной величине x0 такое, что начиная с x0, функция возрастает/убывает монотонно. Но я тупой и не знаю как. А другим пофиг на вопросы школьников.
Это же алгебраические дополнения соответствующих элементов, не?
Помогите с математической индукцией с неравенствами. Как доказывать, преобразовывть неравенства? Если при уравнении можно просто сделать замену, ведь мы принимаем уравнение за верное то тут я хз как преобразовавать. Пробовал и факториалы раскрывать, никакой закономерности не вижу, общего делителя не нахожу.
во-первых, у тебя ошибка в степени индукционного перехода справа, там n+1, а не n+2. Во вторых, раздели случай n+1 на два множителя, чтобы один из множителей был равен выражению из n случая. Потом просто докажи неравенство для оставшегося
Вот тебе наброски древних людей об этой задаче https://puu.sh/xu1tz/80637bb9fe.png
Падажи, это что за наскальные надписи?
намек на то, как собственно доказывать последнее неравенство. это произведение от n+1 до 2n+2
Ну пиздец, нам на паре это дали вообще дали без алгебраической суммы и произведения, узнал что значат эти закорючки когда домой пришел. Видимо надо сначала курить их. Кстати, как называется "С", который показывает сколько есть подмножеств k элементов в n множестве?
жиза. ты из дс универа? тоже с математической индукцией не особо. доказывали бином ньютона и еще какую-то парашу
Дс-2. Тот же бином, хех. Я думала вообще начнем с интегралов, готовился к ним. По лекции вообще теория множеств и дискретка была. Они там вообще координируют учебный процесс?
сочетания называется
Анон, поясни, хули так?
тэкс. три икс к кубе плюс константа. получается второй замечательный предел надо юзать
Пиздабол, там не то в ответе. Учи матан.
А вот ты вроде прав. э
Как быстро надрочиться видеть все эти трансформации и возможные перестановки, если матаном больше пяти лет не занимался?
задача из линейного программирования. пик.
R должно быть между 5R и 7R.
получается система:
7R - 5 >= 0
5R - 4 <= 0
|4R - 3| >= 0
минимизировать R.
получается R = 3/4.
не правильно?
на глаз, можно найти минимум на графике: |7R - 5| + |5R - 4| + |4R - 3|
задача из: http://kvant.mccme.ru/1975/10/fizika_i_linejnye_neravenstva.htm
R должно быть между 5R и 7R.
получается система:
7R - 5 >= 0
5R - 4 <= 0
|4R - 3| >= 0
минимизировать R.
получается R = 3/4.
не правильно?
на глаз, можно найти минимум на графике: |7R - 5| + |5R - 4| + |4R - 3|
задача из: http://kvant.mccme.ru/1975/10/fizika_i_linejnye_neravenstva.htm
>R должно быть между 5R и 7R.
опс. R должно быть между U3/I3 и U2/I2.
как решить?
он тебе правильный ответ подсказал. просто сделать привязки в уме. если есть степень, значит мб этот предел итд
Попробуй линейную регрессию.
А почему у тебя "=" вместо стрелочки?
Где можно почитать про матрицы и определители? Ибо для меня это какая-то ебанутая игра в шахматы. Желательно с разъяснениями почему это работает.
Винберг.
линейная регрессия с линейным программированием:
r - (U_i - I_i R) ≥ 0
r + (U_i - I_i R) ≥ 0
минимизировать для r.
похоже на:
r = sum |U_i - I_i R|
если раскрыть модуль:
r = sum(U_i - I_i R) и r = sum(I_i R - U_i)
https://math.stackexchange.com/questions/47944/linear-regression-for-minimizing-the-maximum-of-the-residuals
Объясните, пожалуйста, почему в доказательстве существования квадратного корня в множество S = {y ∈ R | y > 0 && y^2 < x} не входит непосредственно y = sqrt(x)? Почему, несмотря на то, что в доказательстве выводится, что L (L^2 = x) - точная верхняя граница множества S, это же самое L не попадает в множество S из-за строгого неравенства y^2 < x?
Ссылка на доказательство: http://planetmath.org/existenceofsquarerootsofnonnegativerealnumbers
Ссылка на доказательство: http://planetmath.org/existenceofsquarerootsofnonnegativerealnumbers
Является ли кватернион решениеv какого-либо вещественного уравнения, как x^2=-1 => x=i?
Не могу понять, сходится ли ряд, вольфрам тоже не может.
Ну, там lim=0, если тебе это поможет.
Я нихуя не понял в этом доказательстве. Есть ведь дедекиндовы сечения и принцип разделяющего числа, что же ещё надо?
lim чего? Последовательности cos2(2n) / n?
Судя по всему, недостаточно сказать, что если у нас есть A = {a ∈ R | a > 0 && a < x^2} и B = {b ∈ R | b > x^2}, то разделяющее их число L будет удовлетворять L^2 == x. Там и доказывается, что L^2 действительно в этом случае равен x. Последнее довольно очевидно, но, судя по всему, недостаточно.
Переформулирую свой вопрос. Может ли быть такое, что точная верхняя граница S = {a ∈ R | a^2 < 2} будет равна a = sqrt(2)? В данном случае a не входит в S, но, несмотря на это, в доказательстве выводится, что sup S == a == sqrt(2)
https://math.stackexchange.com/questions/1415235/prove-the-existence-of-the-square-root-of-2
общий член, u_n -- штука под знаком сигмы, стремится к нули, при n -> inf, значит ряд сходится.
блин, нет.
если ряд сходится, то общий член к нулю. обратно не всегда верно.
sum(1/n) расходится, например
нельзя показать, что ряд расходится зная что среднее cos^2(n) = 1/2
sum 1/(2n) расходится.
>matlab
Что это за теорема?
maxima.
я думаю ряд cos^2(n^2)/n расходится.
cos^2(n^2) = 1 - sin^2(n^2)
sum 1/n - sin^2(n^2)/n
левая часть суммы расходится.
или так нельзя?
Здесь какой-то бред
Подкиньте гайд как прокачать логичность мышления и смочь в понимание доказательства теоремы Пифагора.
Что там понимать? Самое просто доказательство - через вписанный и описанный квадрат, гугли.
Пока не понимаю.
Начни геометрию с начала.
среднее cos^2(n) = 1/2?
ищи среднее значение функции.
это же вопросы.
а второе почему бред?
если sum(u_n + v_n)
и sum(u_n) расходится, то sum(u_n + v_n) может сходится?
Но я ее перестал понимать с 7 класса, когда все эти аксиомы и начались. Там сам по себе нужен навык логического мышления? С другой стороны как же все эти школьники учат это...
Какая разница какое среднее? Тебя спросили теорему о связи среднего значения и предела.
>если sum(u_n + v_n)
и sum(u_n) расходится, то sum(u_n + v_n) может сходится?
да
Хорошая попытка, но нет. Разность двух расходящихся может быть сходящейся. Попробуй через косинус двойного угла, помню на семинарах по матану как-то так решалось.
>среднее cos^2(n) = 1/2?
>ищи среднее значение функции.
Это название теоремы? Или ее доказательство? Я вот в матане очень слаб, может действительно не помню такой теоремы.
Школьная геометрия призвана, чтобы учить логически мыслить, совет попробуй с начала самый дельный, который тут могут дать. Дело в том, что нормально человеку сложно представить, как можно не понять это доказательство, а проф педагагов тут нет.
>Школьная геометрия призвана
...напрочь отбить у людей желание заниматься этой хуйнёй.
Кому как. То, что она кому-то не нравится, говорит скорее о проблемах у этого человека. А так простой и приятный предмет, задачи там тем более сейчас на уровне прямо примени теорему. Ну это я так считаю.
Что же в ней не так?
Как человек, который был в классе с математическим углублением и классическим изучением могу сказать, что в классическом обучении геометрия сильно сжата, её можно понять, но если ребёнок действительно одарён или ему интересен материал. В других случаях, как у меня, например,понимание сыпалось на треугольниках, теореме Пифагора и далее по программе. А вернуть те знания довольно-таки трудно. Знания есть, а применения на практике не было из-за банального недопонимания. Зачем проводить прямую, почему на том рисунке треугольник {...}, а не {...}.
>То, что она кому-то не нравится, говорит скорее о проблемах у этого человека.
И эта проблема - сама школьная геометрия. Или способы её преподавания. Более тошнотворной вещи я не встречал. Аутичные игры с убогими фигурками, впихиваемые через силу - вот что такое школьная геометрия.
Я тоже учился геометрии по разным программам, проблем никогда не было ни у меня, ни у некоторых нормально учащихся одноклассников.
Что ты вообще на этой доске забыл?
По-твоему, все, кто не любит школьную геометрию, не должны здесь находиться?
Да
Можешь смелее рассуждать в том же духе. Например, "не уважаешь армию/тюрьму - не мужик, вон из нашей четкой компашки", "не уважаешь Путина - враг народа, вон из страны" и прочий нонсенс. Вперёд.
Подозреваю в этом анончике обычного вонаби-математика, со знаниями 8 класса и задачами про множества (которых тут половина).
Где-то тут ходила паста о ненужности школьной геометрии. Мне сложно понять мотивацию людей, которые одновременно считают геометрию "аутичными играми с убогими фигурками", но при этом спокойно воспринимают другую математику. Кто вы и зачем вы занимаетесь матешей?
Где-то тут ходила паста о ненужности школьной геометрии. Мне сложно понять мотивацию людей, которые одновременно считают геометрию "аутичными играми с убогими фигурками", но при этом спокойно воспринимают другую математику. Кто вы и зачем вы занимаетесь матешей?
Я, кстати, тоже не понимаю. К науке математике школьная геометрия ближе всего из школьной программы.
Лол, ты совсем аутист? Хули ты хотел от начинайко-треда, куда заходят самые разные люди с самым разным отношением к математике?
Если я программист, то насколько хорошо я обязан знать математику?
>аутист
Угадываю анона по почерку
Собираюсь смотреть лекции на Лекториуме. Какие подводные?
Начну с этого
https://youtube.com/watch?v=dPw0gI08hOk
Начну с этого
https://youtube.com/watch?v=dPw0gI08hOk
Ты хорошо подумал, Калган?
Сталкер-яндере что ли?
А что не так?
а задани5я каки5е будешь делат6ьТ:?
Не знаю (
ну вот6 наверное еди5нст6венные подводные.
И что делать? Найти задачник и решать? И спрашивать тут
да
да
ли5бо чи5т6ай параллельно учебни5к с упражнени5ями5
к лекци5ям ест6ь конспекты может6 т6ам указанно от6куда они5 берут6 задачи5
Обязан ни на сколько. Если код-макака, знать математику не надо. Если специалист computer science, пригодится может что угодно из математики. В стандартный пак "Прикладная математика и информатика" в вузе входят матан, алгебра, дифуры, дискретка и вычислительные методы. Нагуглить программу можешь сам
Забыл школьную геометрию. Она царица математики по версии ведущих профессоров с двач.хэка
Она может пригодиться в любом проекте, особенно в игровых.
Чел, мы не хотели тебя обидеть, но если ты называешь евклидову геометрию игрой в бисер, ты можешь назвать таковой что угодно в математике
Она судя по всему дает значительный прирост в мышлении.
>Нагуглить программу можешь сам
Да, на их много. Какую лучше брать за пример?
Что угодно в математике лишено смысла и делается по приколу. Но планиметрия и стереометрия это не прикольно ни разу.
Вербита
Ты сначала скажи нам какой ты программист, что уже умеешь, что хочешь научиться.
Алсо ответ прост, что-то не понимаешь - гуглишь - читаешь.
Ок, ок, ок. Тебе не нравится, мы поняли.
Так именно, что я новичок и не хочется, как бы это сказать, в грязь упасть, в общем. Нормальным программистом хочу стать, а не веб.
Очередной довен квешн на вашей доске матанонебожителей.
Прошу объяснить мне как из объведеного выражения получилась 1/2(хотя бы сказать какая это тема чтобы я почитал)
и причем тут p/2 и p/6
Спасибо.
Прошу объяснить мне как из объведеного выражения получилась 1/2(хотя бы сказать какая это тема чтобы я почитал)
и причем тут p/2 и p/6
Спасибо.
>мы
Уходите в свой оснований-тред. От вас никакой реальной помощи и подсказок не дождёшься, только мутные срачи с умным видом.
Это тригонометрия называется.
можешь поподробнее
Дисциплина в математике, которая изучает отношения сторон треугольника. На твоём скриншоте тригонометрическое уравнение с областью определения.
спасибо
пойду выучу тригонометрию
Давай, в факе есть учебник по тригонометрии, кстати, можешь его попробовать.
В первой системе в первом уравнении переносишь в правую часть вычитаемое, сокращаешь обе части и получаешь первое уравнение во второй системе. Обычное тригонометрическое уравнение, которые разбираются в сборнике Сканави
Перед кем ты собираешься падать в грязь лицом, если учишься один дома?
Ты о чем? Я помогаю во всем, что знаю, вон с рядом что смог посоветовал. Алсо я не знаю о чем основания тред, но я занимаюсь логикой. Мне стоит туда идти?
Поехавший.
Лямбда-исчисление, конструктивизм, теория типов, теория категорий. Логика.
Потом работать же.
Прости, но для работы тебе нужно уметь программировать, а не знать достаточный уровень матеши, чтобы научиться программировать.
>Нормальным программистом
Ну значит код-макакой.
читай
Я понимаю, поэтому и спросил про обязательный уровень.
Основ гамологической алгебры должно хватить.
>Я понимаю
>пишет противоположное
Еще раз говорю. Если ты хочешь стать программистом, то ты становишься им, по ходу дела понимая, что тебе надо изучить по математике, а не наоборот. Сейчас тебе тут насоветуют всякого, а хоть раз тебе от этого понадобится процент, да и то, придется повторять, потому что ты все к хуям забыл.
А вообще заебали вкатывальщики. В говнокодерстве проблем намного больше, чем выглядеть дураком перед колегами.
Вот тебя двачую. Понадобится что-то - выучишь, рили.
У нас в универе было четыре сема ебучего матана и только потом один сем изредка показывали, как его можно юзать. Нахуя оно такое нужно, а?
вот доказательство для схожего ряда:
https://math.stackexchange.com/questions/2160951/sin2-n-n-series-when-sin-is-defined-on-complex-numbers
я немного добавлю.
перепишем ряд cos(n^2)^2/n так:
1/(2n) + cos(2n^2)/(2n) -- известное тригоном. тождество
теорема: если sum(a_n) расходится, sum(b_n) сходится, то sum(a_n + b_n) расходится.
можно доказать из теоремы: если sum(a_b) сходится и sum(b_n) сходится, то sum(a_n +/- b_n) сходится.
так-как 1/(2n) расходится, то достаточно доказать, что cos(2n^2)/(2n) сходится.
признак Дирихле:
https://en.wikipedia.org/wiki/Dirichlet's_test
так-как
e^(jn) = cos(n) + j sin(n) -- формула Эулера
то
cos(2n^2) = R {e^(2jn^2)} -- реальная часть комплексного числа.
наш ряд теперь выглядит:
sum(1/(2n) + 1/(2n) R {e^(2jn^2)}) -- все это для Дирихле
можно R вынести за сумму. не знаю почему.
a_n b_n = 1/(2n) e^(2jn^2)
Дирихле:
1. a_{n + 1} < a_n
2. для b_n грань 2.
значит a_n b_n сходится.
значит наш ряд расходится.
Абитуриент вкатывается. Есть диф. уравнение: xdy=ydx
Интегрируем и получаем решение ln|y|=ln|x|+C; x=0; y=0
Возьмем y за функцию. Во всех учебниках/решебниках пишут ответ y=C'x
Какого хуя они модули убирают?
Интегрируем и получаем решение ln|y|=ln|x|+C; x=0; y=0
Возьмем y за функцию. Во всех учебниках/решебниках пишут ответ y=C'x
Какого хуя они модули убирают?
C - это произвольное число, которое может быть и отрицательным.
Подскажите, пожалуйста, начало решения в следующей систему дифференциальных уравнений.
z встречается только в одном уравнении?
>простой и приятный предмет, задачи там тем более сейчас на уровне прямо примени теорему
Это все только ухудшает.
Как данное безобразие решается? Я уже что только не делал. И корни в степень преобразовывал, и сокращать всячески пытался, всё равно не могу получить нормального ответа. Даже PhotoMath какой-то длинный завуалированный ответ даёт.
Множества {∅, {∅}} и {{∅}} равны?
>{∅, {∅}}
Это что такое?
Какого хера Дерево не хочет считать сумму? Даже бесплатный Вольфрам взял, ЧЯДНТ?
Умеешь преобразовывать корень в степень?
Единица определённая множеством.
Тогда нет. Пустоем множество - именно множество. Т.е. {∅, {∅}} состоит из двух элементов, одно из которых пустое множество, а другое - непустое, состоящее из одного элемента - пустого. Эти же рассуждения верны, если заменить пустое множество на любое другое.
А что сложного? Корень квадратный - это степень 1/2. И так далее.
Почему говорят об общей алгебре как способе поднятия абстрактности мышления? Что в ней особенного?
Если заменить {∅} на x, то чтобы доказать, что {∅, x} = {x} нужно доказать, что они подмножества друг друга.
1. {x} подмножество {∅, x} т.к. оно имеет только 1 элемент и этот элемент принадлежит другому множеству.
2. множество {∅, x} состоит из двух элементов. Надо доказать что оба эти элемента есть во другом множестве. Первый элемент x. Он есть в другом множестве. Второй элемент ∅. Пустое множестве это элемент любого множества. Значит он тоже есть в другом множестве.
Значит эти два множества равны.
Забыл сказать, что говорим про наивную теорию множеств.
Преобразуй все корни в степени.
Очевидно, мне это не помогло.
>Пустое множестве это элемент любого множества.
Я, конечно, в мат логике только начинаю делать первые шаги, но здесь слово элемент надо заменить на подмножество, а если это сделать, то доказательство будет невернум.
Это множество. Ваш КО
Ты умеешь работать со степенями? Там знаешь таблички, свойства степеней.
Естественно.
Пустое множество - это подмножество любого множества, а не элемент, строго говоря.
Покажи что у тебя получилось, после того как ты превратил корни в степени сделал все что мог, чтобы упростить эти степени по их св-вам.
А, ну да, там опечатка, разумеется.
Где конкретно?
Да хер его знает, может там деление?
нет
Что, тут никто не пользует инструменты белого человека?
Причем если задать точность n цифр после запятой, всё ок почему-то, даже если n=9000
Может лимит посчитаешь?
Он сходящийся один хуй.
Помогите мне пожалуйста. Не получается решить эту систему с 5 неизвестными,ничего не получается выразить, подскажите пожалуйста, возможно её решить вообще? Или эта система является несовместной? И если можно её решить, то подскажите как. Потому что если даже домножить первое уравнение на x, второе на у и третье на z, сложить, устраняется мю, но после этого всё равно дальше ничего у меня не получается.
Аноны, в решении суммы ряда на всем известном сайте есть пикрил. Правильно ли я понимаю, что 1/20 сократится следующим за ней а, и это справедливо для любого а и а+1, а т.к. сумма у нас бесконечная, то эту 1/20 он просто вычеркнул?
Если прировнять попарно первые три ур-ия, то, что получится?
да, остаются первое, третье слагаемое и в конце два
ну вот что получилось, но из этого мне не понятно как дальше что выразить
Для Вольфрама и Мэпла -1^n != (-1)^n. Чому так? Какая из этих записей эквивалентна минус двойке в степени n (специально написал буквами, потому что разницу между двумя первыми не понимаю, и не хочу ошибиться в записи)?
Хм. И справа и слева 2, альфы какие-то, действительно, что же делать. Я думаю делать вот что: набить руку на сотне другой примеров из любого задачника по школьной математике, а не хвататься за системы из 5 ур-ий.
А, ну если прям очень хочется, то я скажу слово "группировка".
сосач, помоги
такая хуйня
завтра сдавать работу по теме матрицы
в первый раз у меня не приняли
я перерешал три раза и еще два раза на разных матричных калькуляторах и получается тоже самое
помоги, сосач
такая хуйня
завтра сдавать работу по теме матрицы
в первый раз у меня не приняли
я перерешал три раза и еще два раза на разных матричных калькуляторах и получается тоже самое
помоги, сосач
\mu = 1/6 . Кинешь мне 1200 денег на киви - вышлю полное подробное решение в .pdf
Тебя ебут. Все верно. Подойд к преподу и спроси: почему вам нравится ебать молодых первокурсников?
Чо значит не приняли, за такую хуйню надо пояснять.
Существует способ выбора абсолютно случайного действительного числа на выбранном отрезке? И если да, то выбранное число всегда будет трансцендентным и вообще не принадлежащим ни одному заданному наперёд счётному множеству?
Дай определение случайного числа
Хотя я понял. Да есть. Луркай аксиома индукции
Приоритет операций?
Как бы да, но странно прост.
Что странного?
вот, после группировки получилось такое, и выходит, что x=y=z
может эта система из 5 уравнений является несовместной, потому что как такое возможно что сумма квадратов этих чисел равна 1, то есть x^2=y^2=z^2=1/3, а сумма x+y+z=0? Вообще, имеет эта система решение? И если она всё-таки совместна, то как делать дальше?
но у меня нет денег(
Подсказка, система очевидно несовместна, и ты даже написал почему.
блин(((
первоначально, это была задача нахождения экстремумов функции 3 переменных с 2 ограничениями методом множителей Лагранжа, то есть составляем функцию Лагранжа, находим частные производные, и потом получаем систему 5 неизвестными. Выходит, что эту задачу нельзя решить? А можно было бы сразу как-то понять, что эта задача не имеет решений? Эти 2 ограничения изначально что ли не являются совместными?
Не тупи, она совместна. Тебе нужно решать уравнение ax = 0 не х = 0, а либо а=0, либо х=0
То есть первое равенство выполняется тогда, когда либо х=у, либо z=2 \lambda.
Как вычислять функции Матье? Мне нужно решить с помощью различных численных методов уравнение y''+ych(x)=0, y(0)=0, y(2.2)=1, чтобы было с чем сравнивать результат мне нужно аналитическое решение, Вольфрам Альфа говорит мне, что точное решение это (4.20766-13.391i)MathieuS[0, 2, ix/2], где MathieuS это нечетная функция Матье, делаю все в Матлабе, там такой функции не нашел, придется реализовывать самому, я так понял это специальная функция, и ее надо считать как-то хитро, в ряды раскладывать или еще как, не подскажите, где можно почитать про это вот все?
Посмотри в первом томе Ландау - параметрический резонанс. Вроде как там есть ряд для функции Матье
> y''+ych(x)=0
Ты и сам можешь построить решение этого уравнени методом асимптотической сшивки: в х=0 это осциллятор, в х это бессель от экспоненты. Вангую, что тебе понадобится всего 5-10 членов разложения коэффициена сшивки
>Посмотри в первом томе Ландау
Это первый том "Теоретической физики" Ландау и Лифшица?
>методом асимптотической сшивки:
Что это за метод?
Аноны, вот есть теорема Абеля-Руффини, её по идее можно использовать в криптографии, ключ пять чисел, по нему строится уравнение 5 степени и обратно из уравнения ты не получишь иксы. Или получишь? В чём подвох в общем, так же по идее можно шифрование сделать, которое невозможно взломать.
Не стоит лезть туда, в чем не разбираешься. Можешь попросить решить вольфрам уравнение 5 степени.
>Можешь попросить решить вольфрам уравнение 5 степени.
Даа, я уже. Тогда о чём та теорема? Типа нет общей формулы, но x найти можно численно?
Написано же в вики, не выражается в радикалах, не больше ни меньше. И собсно еще один вопрос. Твой охуительный алгоритм даже если бы и работал, то был бы бессмысленным.
Алиса может зашифровать сообщение, отправить его, а потом сама же и расшифровать, Боб этого сделать не может, потому что не знает ключей. Значит Алисе придется искать защищенный канал, чтобы переслать сообщение бобу, а в таких условиях можно придумать и более быстрые и более защищенный алгоритмы.
>Боб этого сделать не может, потому что не знает ключей.
Ключи передаются ИРЛ на бумажке,
Ладно, я понял, в общем, хуйня идея. Спасибо.
Ага, это называется защищенный канал. В реалиях нашей жизни я не хочу ездить к владельцу каждого сайта даже один раз, чтобы отдать ему свои ключи.
Ну это тип между мной и другом, чтобы провайдер не запалил, что пишем.
Тогда норм
Почему бы не использовать стандартные алгоритмы, при которых даже встречаться не нужно с другом? Да и провайдер и так не может палить большую часть трафика.
Хз, можно, но не так интересно/не факт, что разберусь и получится сделать,а тут валялся на диване просто и мысль пришла такая. Типа по 5 числам получается уравнение, потом вместо x подставляю и я и он коды символов, получается таблица и с помощью неё и общаемся.
Есть куча софта для этого, которая в два клика позволит тебе общаться кучей чисел.
Ну софт кто-то другой писал, не так интересно. Ну а вообще, вот пропустил я через уравнение сообщение, получается каша из чисел, какими методами можно узнать, что это за уравнение, какой принцип в общем? Мне кажется это не так уж просто сделать, тем более там большая степень, отличие между например кодом А и Б, скажем 61 и 62 это уже на очень много различаться будет.
>какими методами можно узнать,
Есть какой-то частотный анализ вроде, но мне кажется он не должен работать, пушо слишком разброс большой.
>Упрощённо, частотный анализ предполагает, что частота появления заданной буквы алфавита в достаточно длинных текстах одна и та же для разных текстов одного языка. При этом, в случае моноалфавитного шифрования, если в шифротексте будет символ с аналогичной вероятностью появления, то можно предположить, что он и является указанной зашифрованной буквой. Аналогичные рассуждения применяются к биграммам (двубуквенным последовательностям), триграммам и т. д. в случае полиалфавитных шифров.
Хотя будет, да. Ладно, хуйня идея в общем. Спасибо за ответы.
А как ты собрался шифровать то уравнением?
Ну например есть пять чисел 2,3,5,7,11, я их передаю другу на бумажке, у него вот это будет (x-2)(x-3)(x-5)(x-7)(x-11), раскрывает скобки(1 пик). Потом например у a это 61 в hex, подставляется в уравнение получается число на 2 пике. И так для каждого символа составляется словарь у меня и у него на компе.
>например у a это 61 в hex,
ASCII код.
Возможно ли доказать без аксиомы выбора, что все гамалогии натуральных чисел нулевые?
Очень маловероятно (p<0.05). В любом случае, советую покопать в сторону теоремы индукции.
Не очень понял, ты передаешь другу корни уравнения. А дальше что?
Просто подставить 61 многочлен? А зачем тогда знать корни его?
Что можно почитать на счёт теоремы индукции?
Рекомендую работы Коэна и Гёделя. Они вроде как раз с помощью неё и доказали существование и уникальность гамалогий и когамалогий.
Хочешь стать маленьким конструктивистопетушком?
Думаю с аксиомой выбора не получится.
При каждом a найти решение ОДУ
y' = (x^2+y^5) * cos (ln y)
при начальных условиях
y(2) = e ^ (pi/2)
y'(2) = a
Просто так ОДУ не решается, нужно поять при чем здесь задача Коши. Если взять неизвестную функцию за константу, то это будет решением ур-ия(за константу ясную из первого условия задачи Коши, т.е. e^(pi/2)). Но как это поможет решить в общем случае непонятно. Ну да, при а=0 решение найдено и больше нет, а что делать в остальных случаях?
y' = (x^2+y^5) * cos (ln y)
при начальных условиях
y(2) = e ^ (pi/2)
y'(2) = a
Просто так ОДУ не решается, нужно поять при чем здесь задача Коши. Если взять неизвестную функцию за константу, то это будет решением ур-ия(за константу ясную из первого условия задачи Коши, т.е. e^(pi/2)). Но как это поможет решить в общем случае непонятно. Ну да, при а=0 решение найдено и больше нет, а что делать в остальных случаях?
Дайте учебников по матану. Фихтенгольц годен?
Сам решил, там же задача Коши полная, значит есть только одно решение.
Дана парабола -х^2+900.
Требуется найти наибольшую площадь ВПИСАННОЙ трапеции и наименьшую площадь ОПИСАННОЙ.
Основание трапеции находится на оси иксов в точках пересечения параболы этой оси, (-30:30)
С какой стороны подступиться к это задаче?
Требуется найти наибольшую площадь ВПИСАННОЙ трапеции и наименьшую площадь ОПИСАННОЙ.
Основание трапеции находится на оси иксов в точках пересечения параболы этой оси, (-30:30)
С какой стороны подступиться к это задаче?
Нахуя нужны группы гомотопий если гамалогии делают всё то же самое но проще?
для вписанной.
площадь аддитивна. можно найти площать трапеции только права под графиком и умножить на два:
y' = -x^2 + 900
S_п = xy' -- площадь прямоугольника под графиком
S_т -- (30 - x)y'/2 -- площадь треугольника.
S = 2(S_п + S_т)
найди максимум S.
не знаю зачем я написал про аддитивность.
> S_т -- (30 - x)y'/2
S_т = (30 - x)y'/2
нарисуй трапецию по правую сторону под графиком и будет понятно.
>
Ты же понимаешь, что это не задача Коши?
Кто здесь шарит в Киселева? У нее есть книга называется "Арифметика", так вот, какой промежуток школы она покрывает? Т.е сколько классов?
Шесть
Это она. Есть уравнение первого порядка и условие на неизвестую функцию.
Нет, это не она. Посмотри внимательней.
Двач, дали темы для курсовой. Что из этого не слишком сложно? Горят лабы по другим предметам, да и не хочется с курсовой по матану сидеть весь семестр. Спасайте.
Матанач, оцени курс линала у нас в шараге
https://vk.com/doc192074917_450422232?hash=98c04b1e55c2ebddaa&dl=e78e21635088275ca9
https://vk.com/doc192074917_450422232?hash=98c04b1e55c2ebddaa&dl=e78e21635088275ca9
Спасибо тебе, кисик.
Зря ты так.
В моём заведении нет ни математики, ни ПМ, ни МиКС.
А есть ПМИ, за которым скрываются программирование.
Вот это уж действительно шарага.
Говно. Гамалогий нет.
>Глава 8. АЛГЕБРАИЧЕСКИЕ СТРУКТУРЫ
>Глава 8.
Говно.
Непрерывность есть. Условие на функцию n-1 т.е. только на саму функцию есть. Это задача Коши и значит можем применить теорему о единственности.
>Непрерывность есть
Докажи.
Толстяк, у тебя ничего не выйдет.
Я понимаю, что тебе это сложно даётся. Но это ничего, интегралы вычислять тоже кто-то должен.
Но задача Коши это из раздела про интегралы, долбоеб.
Зачем ориентировать симплексы чтобы построить гамалогию?
Я не замаричиваюсь о таких вещах, просто рисую тапалогическое пространство и считаю гамалогии (на глаз).
Так из корней получаются коэффициенты же.
На самом деле это довольно нетривиальное дело доказать. Трансфинитная индукция нужна.
Что? Ты мне отвечаешь или постом ошибся? Перемножаешь и получаешь коэффициенты, ну скобки раскрываешь какая трансфинитная индукция лол.
Какие (ко)гамалогии у этого топологического пространства?
хуиные
Заканчиваю магистратуру и интересуюсь, а есть ли смысл идти в аспирантуру если просто нравится учиться математике и в будущем хочется иногда просто писать (и публиковать) не особо углублённые работы, но не нравится перспектива "научной карьеры" c написанием отчётов и преподаванием долбоёбам калькулюса? Или опубликоваться без привязки к какой-либо когорте не выйдет?
Двачую годный вопрос. (сам думаю, что с твоего уровня всё-таки лучше применять твои знания в бизнесе, желательно в личном)
Не очень понял. Вот есть я и ты. Мы знаем корни уравнения. Что нужно делать чтобы зашифровать и расшифровать данные? Алсо не обращай внимания на посты про гамалогии, индукцию и прочее, местные ебланы считают это очень смешным.
> Cartesian product {∅,{∅}} * {∅}
Какой результат?
Например для двух, знаем два числа 3 и 5, (x-3)(x-5), раскрываем получаем x2-8x+15, потом можно каждую букву подставить вместо x и получить её код и тебе и мне, получится таблица кодов, по ней и общаться. Тоже самое, только для 5 чисел. Из чисел получается уравнение(раскрытием скобок), из уравнения таблица символов.
Но тогда получится обычный шифр замены, где мы каждую букву меняем на какой-то набор символов. Он уязвим к частотному анализу, а что самое главное, непонятно зачем вся эта муть с корнями, если можно просто обменяться алфавитами.
>Но тогда получится обычный шифр замены, где мы каждую букву меняем на какой-то набор символов. Он уязвим к частотному анализу
Да, я ещё в среду понял
> если можно просто обменяться алфавитами.
Ну так всего 5 чисел нужно, а так целыми алфавитами меняться.
>Ну так всего 5 чисел нужно
Вам еще нужна одинаковая таблица символов, которая кодирует буквы. По факту, обычный обмен алфавитом. Я понял твою идею, что ascii таблица у всех уже есть, но это имеет к криптографии такое же отношение, как идея называть вместо слова "бомба" слово "картошычка"
Это я тоже ещё в среду понял, лол, просто основная идея была в том, что я думал, что из уравнений выше 4 степени не получить корни и про частотный анализ не задумывался. После гугления гениального и простого RSA мне как-то и писать больше об этом неловко. Плюс там ещё каждая следующая буква зависит от предыдущей, да ещё вначале добавляется рандомный мусор, так что вообще нихера частотный анализ не даст.
Ты очень хуево учил математику (особенно теорвер) если думаешь о том что можно что-то успешно применять в бизнесе.
{(∅,∅),({∅},∅)}
Вот есть тут треды каких то эмотивизмов с основаниями математики, это как я понял разные концепции математики да? А чём разница? какой учат в школе ?
Может там и спросишь?
Мне та мне отвечают. Говорят с такими вопросами в ред ньфагов.
Что-то я не вижу.
А подробнее?
Нашел у себя формулу, не могу догнать как прийти к результату?
Возведи в квадрат. Это вроде называется радикалами или формулой радикалов.
> радикал это корень
Спасибо, кэп.
2 клика в гугле по запросу формула радикала математика, и мы узнаем, что перед нами формула сложного радикала, погуглив про которую находим статью в вики. Если тебе все так очевидно, то почему ты спрашиваешь?
Спасибо, анон.
x^2 - (x + 2)^2 = 8
У меня выходит x=2, но если подставить, то 8 не получается.
У меня выходит x=2, но если подставить, то 8 не получается.
>У меня выходит x=2
Это как выходит?
x^2 - x^2 - 4x - 4 = -x - 4 =8
>x^2 - x^2 - 4x - 4 = -x - 4
>- 4x= -x
>-x - 4 =8
>У меня выходит x=2
Алсо я все так же нихуя не понял, только теперь еще больше.
бамп
Как меняются частные производные функции нескольких пременных при переходе к новым переменным?
По матрице Якоби они меняются
Не понял.
Матрица якоби это же просто матрица частных производных. Там есть, конечно, теория замены переменных, но я примерно и хочу понять как она получается.
Стоит ли учить интегралы и всё что с ними связано? Является ли это математикой?
Устарело давно. Стоит, если интересуешься историей математики.
Нет, не является. Если ты видишь где-то натуральные числа, это тоже история математики и нигде не используется. Ракеты давно летают на алгебраической топологии, а люди считают предметы кагамалагиями де Рама
Ладно, я нашел в матлабе встроенную функцию, чтобы найти достаточно точное численное решение, и остальные, реализованные мною, методы дали близкое к нему решения, такая красота. Однако, я все-таки плохо понял, как вычисляются функции Матье, вообще как применяют специальные функции на практике, вычисляют как сумму рядов?
Спасибо, возможно изучу это в исторических целях.
Я так примерно и думал, вообще не похоже на математику.
Кстати, уже придумали мотивное интегрирование, где вместо этих ваших натуральных чисел кольцо Гротендика.
А геометрическая теория меры появилась еще раньше, и ей решили задачу Плато.
Когомологии де рама к топологии отношения не имеют, кстати, в топологии гомологии сингулярные.
x^2 - (x + 2)^2 = 8
x^2 - (x^2 + 4x + 4) = 8
x^2 - x^2 - 4x - 4 = 8
-4x - 4 = 8
-4x = 12
x = -3
______
(-3)^2 - (-3 + 2)^2 = 8
9 - 1 = 8
8 = 8
Вероятность того, что яблоко червивое - р
Какова вероятность того, что в некоем наборе яблок червивых меньше или равно 10%?
Какова вероятность того, что в некоем наборе яблок червивых меньше или равно 10%?
Всегда останавливаюсь на моменте, когда в решении задачи говорится, что зелёныйугол - это синус. И у меня сразу возникает вопрос: почему именно синус, а не косинус? Или вообще тангенс или котангенс? Объясните, господа.
Угол – это угол; синус – это синус. Если говорится, что угол - это синус, подразумевается, наверно, что в рассматриваемом случае нужен синус угла.
Это говорится в решении задачи, изначально не было ничего сказано про то, какой это угол: синус, косинус, тангенс или котангенс.
Угол – это угол; синус – это гамалогия угла. Косинус - это когамалогия угла. Если говорится, что угол - это гамалогия, подразумевается, наверно, что в рассматриваемом случае нужна гамалогия угла.
А теперь сформулируй для уровня десятого класса.
Ты же понимаешь, что у каждого угла есть синус, косинус, тангенс и котангенс? Точнее, тангенса нет у П/2+Пn, а котангенса нет у Пn, но не суть.
Это уровень десятого класса. Гамалогии в конце него как раз и изучают.
Да, понимаю, и здесь вопрос: почему именно синус, а не косинус, тангенс или котангенс? В задаче ничего про это не даётся.
Синусы-косинусы в физических задачах нужны, чтобы находить проекции сил куда-то. Если ты умножишь силу натяжения на синус этого угла, то получишь проекцию силы на горизонтальную ось.
Так, хорошо, а чтобы получить проекцию на ось OY, нужно умножить косинус на силу? И для чего тогда используется тангенс или котангенс?
нужно знать распределение.
см. пик с кубиками.
по оси S, это сумма чисел на двух костях. если тебе интересно, какова вероятность, что выпадет сумма: 2 или 3 или 4? иначе: сумма меньше или равна 4.
то суммируешь эти вероятности.
так-же можно обозначить S% червивых яблок.
посмотри распределение Бернулли, вроде бы тебе подойдет.
Не помню, чтобы тангенс-котангенс находили применение в физических задачах. Ну сам пошевели мозгами. Что такое синус? Отношение гипотенузы к противолежащему катету. Если мы умножим эту дробь на гипотенузу, силу натяжения, что будет? Гипотенуза сверху и снизу сократится, и мы получим катет. А если то же самое сделаем с косинусом, то получим прилежащий катет. А если будем делить соответствующие катеты на синус или косинус, то, наоборот, сможем найти гипотенузу. Подобным же образом могут использоваться тангенсы-котангенсы.
Тебе выше уже сказали, угол это угол. Возможно в этой задаче используется синус, но вот так вот, без всего мы не можем тебе сказать, что происходит.
пик забыл.
>Не помню, чтобы тангенс-котангенс находили применение в физических задачах
>сила трения
>Что такое синус?
Видимо, я непонятно объяснил. В задаче изначально не даётся даже намёка на угол, с чего я должен решить, что это синус?
Если не дается намека на угол, значит и намека на синус быть не может, потому что синус сам по себе не бывает. Задачу в студию.
Здесь ответ: 10/х? (Да я знаю, что это школьный пример, но почему-то в ответах совсем другое значение).
Как находить гамалогию рациональных чисел?
И что тебе непонятно?
Принцип определения. Неужели всё так легко: чтобы найти проекцию на горизонтали - синус, на вертикали - косинус?
Сап. Сижу за химией. В учебнике написано:
"Преобразуем уравнение Оствальда в квадратное уравнение относительно а:
а^2с + аК - К = 0"
Уравнение Оствальда: К=а^2*с/1-а
Где К - константа диссоциации, с - концентрация, а - степень диссоциации.
Чисто матан, поэтому сюда.
Объясните, плз, по какому принципу происходит преобразование.
>Не помню, чтобы тангенс-котангенс находили применение в физических задачах
Это чисто теоретические изыскания господ Математиков. Игра в бисер чистой воды.
Здесь задача сводится к нумерации всех рациональных чисел. Там короче рисуешь их в таблицу и обходишь по диагоналям. А когда пересчитаешь их, находишь гамалогию натуральных чисел через индукцию
Уравнение Оствальда с двух сторон домножили на 1-а
Большое спасибо
>Там короче рисуешь их в таблицу и обходишь по диагоналям.
Нарисовал. Обошёл. Но гамалогий что-то не видно.
Тут лемма Ферма-Цорна требуется.
Тебе стоит почитать определения синуса и косинуса, после чего тебе самому станет очевидно, как найти проекции. Ну и еще принцип суперпозиции для сил.
В какой системе аксиом?
Совет:
Не ведись на здешние мемы если ты не толстяк конечно.
В ZF, но без аксиомы бесконечности.
Извините, но это уже совсем бред. Куда смотрит модератник, если без трансфинитной индукции все равно ничего не выйдет.
Как доказать самое правое неравенство с картинки?
да.
Любую ли функцию можно представить в виде ряда? Работает ли это для функций многих переменных?
Мне интересно, а какой тогда ответ? Проверил, тоже 10/x получил.
Сап. Подскажите где можно прочитать про операции на графах в матричном виде. Конкретно интересует композиция и декартово произведение. Просмотрел 5 книг - ни в 1 нету того что нужно.
У меня есть работа в которой, грубо говоря, исследуется параметрический резонанс. Мы там много всякой ахинеи про монодромии и когомологии пишем, но в итоге считаем функции Матье так, как написано в Ландау. Но там немного другое уравнение: $\omega^2(t) = 1 - \epsilon sin(\mu t) $
Доброго времени суток двачя, нуждаюсь в твоей помощи, некоторое время назад прочитал книжку по теории вероятности и там увидел хороший термин, короткое название случайной величины, которая равна количеству очков выпадающих на игральных костях. И я его благополучно забыл. Скину на счёт сотку тому кто скажет этот термин и источник откуда он
Читаю Зорича, дано определение , что f - дифференцируемая, если f(x+h) - f(x) = A(x)h + α(x;h) . h , как я понимаю, линейный оператор, h -> A(x)h , а α(x;h)=o(h), h->0. Не могу понять, что имеет ввиду под α(x;h) .
Лучше не вникай. Здесь переплетается с будущими темами и сделано кривовато. а(х, h) - это какое-то о(h), но сама производная это функция от х. И если ты находишь проиводную в разных точках, функция а(х, h) тоже меняется. Именно это и выражает зависимость от двух переменных.
Можешь подробнее? Не совсем тебя понял. Я просто про интегралы спрашивал. На здешние мемы мне плевать.
Интересует один вопрос. А правда ли, что некоторые люди могут считать гомологии тапалогического пространства на глаз? Ну то есть по одному рисунку.
Помогите
Сап. Объясните плиз, как преобразовывается квадратное уравнение с пикрила для решения функции?
Сап. Объясните плиз, как преобразовывается квадратное уравнение с пикрила для решения функции?
А точнее, как раскладывается.
Вы уже изучали трансфинитную индукцию?
Нет еще
А гамалогии?
9 класс
Как можно это доказать?
Возможно ли получить теорему индукции по целым числам если взять бинарное произведение теоремы индукции по натуральным числам?
А что, если взять несчётное произведение? Получим ли мы тогда индукцию по ординалам?
А что, если взять несчётное произведение? Получим ли мы тогда индукцию по ординалам?
Гамалогии AB и CD нулевые. Следовательно, гамалогии ABCD тоже нулевые.
Из чего следует, что когамалогии точки М нулевые. А это значит именно то, что точка М равноудалена от прямых AB, AD и CD.
>Гамалогии
>когамалогии
что это блять такое
На уроках нужно было внимательнее слушать. А так доказательство на самом деле верное.
мимо
не рассказывали про такое )
В девятом точно уже рассказывают.
ну я в девятом и пока точно не рассказывали
То доказательство в любом случае верное. Можешь его и написать.
Только в нечётком множестве кольца гамалогий.
Это легко следует из существования несчётного количества недостижимых кардиналов.
А если у меня класс всех модулей и их гамалогий?
Возможно ли ZF представить в виде тапалогического пространства?
Да, но там через трапеции
Гамалогии ZF уже известны?
бамп
как это доказать?
дай ссылку на кнуги, откуда это.
или название книги.
Kurt Friedrich Gödel, Homology.
Нихуя не понел
Как зовут этого алгебраического геометра транса, который иногда на форчане мелькал?
Есть тут люди разбирающиеся в алгебраической тапалогии?
Давай, шваль.
Поясните за схему Горнера?
Нихуя не могу понять..
Голова болит..
Нихуя не могу понять..
Голова болит..
Актуально. В целом реквестирую годную литературу по графам, сетям и деревьям, ибо играть в задание "найти ошибку" в ебучей методе говновуза меня заебало.
Как считать ко(гамалогии) тапалогического пространства на глаз?
Ну ка поясни. Я вообще нжинер и программирование мне нужно только для расчетов. Вообще нахрена программистам теория графов?
Многие задачи из реальной жизни можно представить в виде графов. Соответственно решение задачи теории графов, решает много задач из жизни. Примеры лень приводить
не нужно. я нашел доказательство.
Rudin, Principles of mathematical analysis, page 68.
Как сократить?
Сап математач. Объясните нубу, зачем сегодня нужны вообще аналитическе решения дифференциальных уравнений, когда есть методы численного вычисления?
Анализ сам по себе нахуй не нужен.
Матемач, я подзастрял на мат моделях.
Каким образом находится АЧХ у систем, когда частоты заданы и когда не заданы? (на пикчах 2 примера с частотами и без)
Каким образом находится АЧХ у систем, когда частоты заданы и когда не заданы? (на пикчах 2 примера с частотами и без)
>Примеры лень приводить
Просто сказал бы, что не знаешь.
Антоша, поясни, на пальцах за Such that ('|') symbol из теории множеств. Чет не могу вдуплить, как оно работает. Спасибо.
Тут на самом деле нужна индукция по ординалам.
Мне нужна помощь с задачами линейного/нелинейного программирования и выпуклыми множествами/функциями (например, нарисовать геометричечкую интерпретацию условий Куна-Такера или решить задачу методом симплекс). Заданий где-то десятка три, и мне нужно немного объяснить как делать первый пример в них и может быть проверить как я справлюсь с остальными. У меня есть картинки милых одетых девочек и может быть что-то еще.
[email protected]
[email protected]
Еблан в треде. Ты блядь, сколько будешь считать интеграл от какого-нибудь запараметризованного решения дифура численно на своей пердушке? Если есть какая-нибудь аналитика (даже асимптотика или галеркин подойдут) ты сделаешь это гораздо и гораздо быстрей, чем численно.
>>25040
>>25042
Какие гамалогии этой цепи постов?
Препод дал задание: изучить, посмотреть материалы касательно функции Строгаца. Что это такое и с чем его едят? (да-да, мне лень вбивать это в гугле и искать самостоятельно, - пока нашел только одного математика Стивена Строгаца, но, вероятнее всего, это не тот чувак).
Что такое "функция" вообще, мэдхаус?
>но, вероятнее всего, это не тот чувак).
Почему решил, что не тот? М.б. именно тот.
Объяснишь, что такое "функция" или нет, лол?
графическая интерпретация зависимости двух переменных
Ку,матемач.
Как будет выглядеть график к этой ебале? И он вообще нужен тут чтобы определить пределы интегрирования?
Как будет выглядеть график к этой ебале? И он вообще нужен тут чтобы определить пределы интегрирования?
Нарисуй вторую гамалогию этой ебалы и там всё видео будет.
У матшкольников уже особые преимущества из-за более ранних занятий? Их уровень вообще возможно догнать?
>матшкольников
Что это такое?
Всякие там пятисемиты и прочие.
Это секта какая-то?
Бампану про Строгаца, очень надо, аноны
Нет, интегралы брать это предел как уже давно известно. Выше не прыгнешь.
Спасибо, конечно, но это книга для детей. И не факт что там про функцию его имени есть. Ну и мне что-нибудь бесплатно и без смс именно про Функцию Строгаца надо.
Чет ступор, матуаны, выручайте
Как выразить n через эпсилон? На паре показали какой-то хитрый околологарифмический ход конем, но тогда я нихуя не вникал. Кстати, мне кажется тут еще хуитка в том, что я неправильно доказываю предел, ведь если эпсилон любое положительное число, то это неравенство не всегда будет соблюдаться...
>Интегралы брать это предел
Кек
Какой "уровень"? Анализ и прочая хуйня это не уровень. Это не математика даже.
Мир -- это некая жидкокристаллическая среда,а математика -- это ее карта?
Кака построить множество действительных чисел с помощью отношения порядка?
Что делать, если не можешь решить задачу? Стоить ли продолжать мучать её самому, или сдаться?
Является ли каждая задача доказательством какой-либо теоремы для частного случая?
Лучше попробовать следующую
Нет, но несколько задач подряд могут доказать что-то общее
Разбираешь частные случаи и показываешь, что для n+1 тоже возможно. Дальше по аксиоме
>не всегда будет соблюдаться
почти никогда не будет соблюдаться, хуйню какую-то написал и рад.
Да я и не рад даже(
Бывает.
Посоветуйте что-то типа введения в формальную логику и вообще посоветуйте материалов как ее познать.
Необходимо построить y = y(x). Выразить y через x у меня не получается. Выходит, что нужно строить y(t) и x(t) отдельно, а потом строить y(x)? Здесь нет способа попроще?
Есть дли задачник по типу Демидовича, только по физике?
Можете посоветовать книжку по теории вероятности, чтобы, с одной стороны, не давили слишком математикой как таковой (потому что бэкграунд слабый, про всякие интегралы и дифференциалы знаю, сдавал зачёт по линейной алгебре (электив был, так факультет даже не технарский), но решать задачи особо не пытался и не хочу. С другой стороны мне и не нужна книжка, в которой бы рассматривались прикладные аспекты статистики. Хотелось бы что-то о природе случайности, чтобы я мог понимать около философские аспекты что ли этого явления.
>чтобы я мог понимать около философские аспекты что ли этого явления
Тебе нужно так ебашить статистику, чтобы зубы отваливались. Почитай Феллера
Батыги и Топтыгин и Гречко
Нужно построить сначала t, потом строить y(t) и x(t) отдельно, а потом строить y(x), а не ту хуйню, что ты сморозил
Как доказать, что все объекты категории множеств являются проективными?
С помощью вот этой штуки
Что это?
Предагаю для начала по теореме о нумерации(использует акс выбора) найти, что для любого множества есть ординал.
Ну а в категории ординалов наверняка каждый обьект -
проективный. Сможешь доказать второе утвержденип?
>использует акс выбора
Ну лемму выбора я уже доказал.
>Сможешь доказать второе утвержденип?
Сейчас докажу непротиворечивость трансфинитной индукции и попробую.
Не уверен, что осилю, но попытаюсь. Если будут вопросы, то сюда припрусь.
Возможно ли на глаз считать когамалогии пространства?
Ты не докажешь непротиворечивость.
Почему же?
Помогите посчитать (ко)гамалогии? Довольно долго сижу уже и не могу разобраться.
Поверхность рода 4.
Тут не понятно откуда растут культи, но тоже аналогично, считай по количеству дырок.
Почему даже не платониками математика считается объективной, ведь математика же не изучает объекты, не проводит эксперименты и всё такое, а просто ебётся с какими то там абстракциями существующими только в головах вчера облысевших обезьян.
Почему только фриков интересует глубинный истинный смысл Математики?
А теперь подумай, это наше простраство похоже на эвклидово просранство, или эвклидово просранство похоже на наше пространство?
Что можно почитать об интегральных преобразованиях и их применении в решении дифференциальных уравнений в частных производных?
Разбираюсь в логарифмами. Попробовал сформулировать своими словами. Поправьте если те так что-то:
"Например, log по основанию 2 (log2) из 32 показывает, сколько раз нужно разделить число 32 на 2, чтобы получилось 2 - 5 раз. Или показывает сколько раз нужно умножить 2 на себя же, чтобы получилось 32."
"Например, log по основанию 2 (log2) из 32 показывает, сколько раз нужно разделить число 32 на 2, чтобы получилось 2 - 5 раз. Или показывает сколько раз нужно умножить 2 на себя же, чтобы получилось 32."
Операция взятия степени в общем случае не эквивалентна умножению числа на себя столько-то раз (ну например как ты умножишь e на себя π раз?).
А так все правильно. Просто логарифмирование это обратная к взятию степени операция, вот и все.
Причём тут наше пространство?
>изучает объекты
изучает математические объекты (в основном структуру)
Как доказать, что целые числа образуют несчётное множество?
1) Почему в доказательстве n = k+1 в правой части добавляют (k+1)? Первый пик.
2) Почему сделали замену 1^2+2^2+...+k^2 на выражение из проверки n=k? Второй пик.
2) Почему сделали замену 1^2+2^2+...+k^2 на выражение из проверки n=k? Второй пик.
ты вообще нехуя не понял про индукцию и пофиксил какой-т хуйней. попробуй заново
лол, блядь, я и так всё доказательство копипастнул. вопрос в том, почему к дроби (k+1) прибавляется
к какой дроби? ощущение, что ты не читал даже то, что копипастнул. картинка из 25119 вообще не имеет отношения к делу. все доказательство в том, чтобы показать, что дробь после шага индукции равна дроби на k-ом шаге + (k+1)^2
как решать самые обычные задачи на составление самых обычных уравнений
Можете посоветовать книжки по теории диффуров
>Операция взятия степени в общем случае не эквивалентна умножению числа на себя столько-то раз (ну например как ты умножишь e на себя π раз?).
Т.е если log2 102 = 6,672, то по моему первому предположению нужно 2 умножить на себя 6,672 раз, что по сути невозможно в виду не целого числа. Да?
А где найти алгебра-2,3 Елагина?
Правда ли что все формулы в математике можно вывести из формул треугольника и сферы?
Правда. Даже аксиома выбора спокойно выводится.
Как называется функция длины периода рациональной дроби?
Через решебник
Это аксиома
Это не доказать и не опровергнуть
Анон прав, ты ничего не понял про индукцию. Прогугли "Математическая индукция" и вопросы отпадут после нескольких ссылок
>Это не доказать и не опровергнуть
Докажи.
Это тоже нельзя ни доказать, ни опровергнуть. А вот это уже можно доказать, но я не помню как
>А вот это уже можно доказать
Докажи что можно доказать.
Лол, что? Это локальный мем такой? По определению, множество Y счётно, если существует f: f(N)=Y, для Y=Z такой будет f(n)=(n-1)(-1^n)/2 для n mod 2 = 1, f(n)=n(-1^n)/2 для n mod 2 = 0; доказательство -- индукция в две стороны (f(n)=z для любого n и n=f^-1(z) для любого z)
Лол, с формальной логикой у тебя всё плохо, причём как со стороны эрудиции, так и со стороны знания основ.
Это постирония?
Это глупость.
Не указана система аксиом + тривиальные ошибки в рассуждениях.
Какая к чёрту система аксиом? Я в явном виде использовал мат. индукцию и более ничего, кроме определений, разве не видно?
Мало того, легко построить доказательство без использования аксиоматики вообще, онли определения (и не тыкай правилом вывода), причём д-во будет конструктивным.
Какие, блядь, ошибки? Укажи хоть на одну. Это просто смешно слышать, задача даже звания тривиальной не достойна. Я учусь на фупме физтеха и за прошлый год на ТФСе и ТРЯПе решал задачки явно посложнее этой, получив 10 и 8 за них соответственно.
Как доказать, что все гаматопические группы (кроме нулевой) ℤ тривиальны? Без аксиомы выбора.
Двач, хэлп. Нужен способ решения подобных задач
Тут легко решается через подсчёт гамалогий. На самом деле это практически тривиально.
Я там преподаю. У тебя реал ошибки, молодой человек.
мимо-препод
Тут как минимум у половины задач нет решения.
Ну, так что за ошибки-то? Научите нерадивого студента.
сап двач. есть что-то чуть прощелучше?ебучего зорича, написанное которым я перестал понимать
Как решить такой предел руками, откуда подступиться? n->infinity
Пробуй посчитать гамалогии предела, если не получится, то считай когамалогии копредела.
Это какой-то тралинг?
Считай производную, применяй лопиталя.
1. в знаменателе: (n + 1)^(n + 1) = n^(n + 1) (1 + 1/n)^(n + 1)
2. число е: (1 + 1/n)^n -> e, n -> inf
3. если нужно найти limit f(g(x)) и f непреревна, то limit f(g(x)) = f(limit g(x)).
Аноны, как доказать Петерсона-Кадаци?
Множество целых чисел счётно.
>Это просто смешно слышать, задача даже звания тривиальной не достойна. Я учусь на фупме физтеха и за прошлый год на ТФСе и ТРЯПе решал задачки явно посложнее этой, получив 10 и 8 за них соответственно.
Зачем нам это знать? Это что-то на уровне
>у меня друзья фсбшники, пизда тебе
может даже и выше
А интегралы вообще можно считать математикой?
(-8)1/3 - получается так нельзя?
Черным по белому написано, что нельзя.
Можно, но ты сначала определи что именно это будет означать.
А почему? У меня в голове не укладывается. И так что ли нельзя: 3√-8?
Не понял тебя. Что будет означать?
Почему мы раскрываем модуль с минусом, если функция на промежутке (3;∞) возрастает? Мы построили гиперболу, сместили ее, а затем отразили относительно икса. Кусочек ветви же теперь по сути возрастает...
есть свойства, как:
(ab)^n = a^n b^n
они всегда верны для a > 0, b > 0.
это свойство не всегда верно для a < 0 и/или b < 0. например:
(-2 (-2))^(1/2) = (-2)^(1/2) (-2)^(1/2)
(-2 (-2)) = 4
для нечетного показателя будет верно. как в твоем примере.
но нужно следить за четностью. да и нужно доказать все эти свойства для нечетных показателей и оснований меньше нуля.
>Почему мы раскрываем модуль с минусом
Потому |x|= x, x=>0; -x,x<0. Функция на промежутке (3,inf) (6/x-2) < 0, значит модуль от нее раскрывается как полагается.
Непонятно
Спасибо, теперь ясно
Как доказать, что из тривиальной фундаментальной группы следует стягиваемость?
нету дырок - нету проблем
Скиньте тот гайд по съёбу на phd заграницу пожалуйста.
homology.com
Как посчитать (ко)гаматопические группы вот этого рисунка?
Нормальногораспределениявопрос
создаю в экселе столбец из 100-та ячеек с заполнением x=(xi-1)+(допустим 1), получаю соответственно столбец чисел от 0 до 100 с шагом 1
в соседнем столбце пишу команду =НОРМ.РАСП(ячейка Xi;среднее значение 50;стандартное отклонение 50; весовая)
и получаю в принципе похожие на правду(судя по графику) значения нормального распределения при таких исходных данных..
НО! суммирую все значения второго столбца-и получаю не 100 и не 1, хотя по моейдноматематической логике должна быть единица, ну или 100, типа процентов.
Объясните плиз почему это не так?
создаю в экселе столбец из 100-та ячеек с заполнением x=(xi-1)+(допустим 1), получаю соответственно столбец чисел от 0 до 100 с шагом 1
в соседнем столбце пишу команду =НОРМ.РАСП(ячейка Xi;среднее значение 50;стандартное отклонение 50; весовая)
и получаю в принципе похожие на правду(судя по графику) значения нормального распределения при таких исходных данных..
НО! суммирую все значения второго столбца-и получаю не 100 и не 1, хотя по моейдноматематической логике должна быть единица, ну или 100, типа процентов.
Объясните плиз почему это не так?
Почему не указаны оси и единичные отрезки?
Скажите что тут делать, какое тут задание. Я не пойму нахуя справа числа даны. Решу сам, ебланы из беседы молчат
ты суммируешь, а не интегрируешь, поэтому есть погрешность
плюс любое число может получиться с ненулевой вероятностью из нормального
Привет, матаны
Такой вопрос.
Есть такое замечательное неравенство Неравенство Хёфдинга, в одном из способов доказательства есть такой пассаж.
Я предельные неравенства уже подзабыл нихуя не знал.
Можете пояснить, какого хуя ТАК КАК, откуда это?
Такой вопрос.
Есть такое замечательное неравенство Неравенство Хёфдинга, в одном из способов доказательства есть такой пассаж.
Я предельные неравенства уже подзабыл нихуя не знал.
Можете пояснить, какого хуя ТАК КАК, откуда это?
Ты несешь какое то своё шаражное говно и думаешь, что кто-то тут как экстрасенс, поймет что там за задания?
>какого хуя ТАК КАК
Что именн так? Равенство или последующее неравенство.
Свободен, аноны! Давайте скинемся и купим!
>ТАК КАК
Матожидание аддитивно.
Они уникальны с точностью до гаматопии.
Это не математика, это хуйня какая-то.
Гомологии -- это псевдонаука.
Это и хорошо, "наука" современная это удел долбоёбов.
И я не про гамалогии говорил, а про гаматопии.
Гомотопия -- это подраздел индукции
Куда идти после того, как закончил школьный курс математики? Мат. логика, теория групп, что-то другое? В списках немного разбросано
Алгебраическая тапалогия.
Желательно начинать с логики. И для начала нужно забыть всю школьную программу, так как это даже математикой не является.
Потом можно изучать всё, что нужно для изучения гамалогии и гаматопии.
Это должно быть плохо?
Что почитать по основам логики? А то не пойму смысла импликации, когда из ложного А следует истинное Б и это все истинно.
>А то не пойму смысла импликации
У классической импликации по сути и нет смысла.
Говорят, что у жизни смысла нет. Тем не менее в учебнике даже выделено "обратите, в частности, внимание на то, что если А ложно, то импликация А=>В всегда истинна". И мне надо это понять.
https://en.wikipedia.org/wiki/Principle_of_explosion
Доказательство работает почти во всех видах логики.
Если ты не тролль, то это такое:
"Если идет дождь, то асфальт на улице становится мокрым"
А = Идет дождь
Б = Асфальт на улице становится мокрым
Сравни различные варианты этого высказывания с таблицей импликации.
Может ли быть так, что "Идет дождь", но "Асфальт не мокрый"? Нет. Потому что это прямо противоречит начальному высказыванию.
Но может ли быть "Не идет дождь", но "Асфальт мокрый". Да. Может быть на асфальте осталась лужа. Это никак не противоречит первоначальному высказыванию. Поэтому
1 -> 0 = 0 Не может быть такого
0 -> 1 = 1 Вполне, че бы и нет
О, спасибо.
> Если ты не тролль
Нет не тролль, просто со не очень сильной подготовкой взялся за университетский курс, по ходу дела закрываю пробелы.
У меня вопрос. Можно ли считать математикой изучение интегралов?
Отвечали уже в этом треде.
>"Если идет дождь, то асфальт на улице становится мокрым"
Что-то мне страшно. Ты откуда этот пример взял? Просто я его выдумал несколько лет назад, вместо вики-примера про РАБотника. Вроде как нигде не писал.
Я в твоей голове сижу можно сказать.
А считание пределов можно назвать математикой?
Ты ебанутый? Ты что там делаешь?
Проверяю тут кое-что. Ты главное сильно не дёргайся.
А полагается ли мне приз за доказательство гипотезы Римана через подсчёт одного очень простого интеграла?
Я попробовал тут один метод и он оказывается сработал.
Я попробовал тут один метод и он оказывается сработал.
Сейчас я тебя запру!
Как доказывать, что гамалогии сфер всех размерностей изоморфны гаматопическим группам?
Сейчас твои теоремы сворую для начала.
Можешь не искать, у меня нет никаких теорем, которые не были бы уже описаны!
Ну с дождём и асфальтом действительно невероятное совпадение.
Кто-нибудь может подсказать, где искать статьи относительно свежие? Желательно уровня <= 3 курса, около 40-50к знаков, на анг языке естественно.
https://arxiv.org/
Все что нашел, но это скорей архив лекций.
https://arxiv.org/
Все что нашел, но это скорей архив лекций.
Архив - это главная площадка для этого дела. Там не только лекции.
Сап, двач. Вкатываюсь в линейную логику, всё в принципе пока понятно, научился доказывать простенькие леммы в рамках ЛЛ. Но вот такой вопрос — как объяснить смысл слов "аддитивная" и "мультипликативная" операция/константа? Я имею ввиду не формально (не просто набор логических правил из определения ЛЛ), а так чтобы какое-то интуитивное понимание было?
помогите мне пожалуйста с теорией вероятности. Допустим у меня есть 2 дискретные случайные величины кси1 и кси2, чья корреляция не равна нулю, то есть эти величины зависимы, подскажите пожалуйста, как находят закон распределения случайных величин ню1=кси1+кси2 и ню2=кси1*кси2?
Перекат
Перекат
Перекат
https://2ch.hk/math/res/25291.html
Переспрашивайте свои вопросы в новом треде.
Перекат
Перекат
https://2ch.hk/math/res/25291.html
Переспрашивайте свои вопросы в новом треде.
Нужно нарисовать график и найти новые пределы интегрирования, то есть свести к повторным интегралам
Извини, но причём тут математика? "пределы интегрирования" к математике не имеют никакого отношения.
помогите построить график. во втором я вынес с сделал квадрат разности. а что с вынесенным х делать? а в верхнем тоже так
>Нужно нарисовать график
Ну так рисуй
>невероятное совпадение
Ну охуеть просто невероятное. Он в каждом засцаном учебнике по логике есть
А как можно формулой задать диапазон? Щас на работе коллега попросил помочь с заданием по информатике для его пиздюка. Задание такое. Нужно составить программу ЛОТЕРЕЯ с тремя выводными строками в первой значения от 1 до 100, во второй от 101 до 200, в третьей от 201 до 250. Я просто написал random (1,100); random (101,200); random (201,250); а училка говорит что неправильно так делать. Надо что бы в условии были заданны переменные с присвоенными им значениями и результат(рандомное значение из диапазона от x до y) получался через формулу.
Используй одноместный рандом. Рандом(3) + 1 - от одного до трех, например.
Как правильно считать x^3*y? А раскладываю по формуле произведения и считаю обе части отдельно, но может есть решение попроще или поуниверсальнее? Например если там будет не произведение, а сложная функция, то всё равно придётся раскладывать до тех пор пока не получится взять дифференциал от одной переменной?
Ты пидорас или педофил?
Берешь и переводишь из неявного вида в явный или берешь производную неявной функции.
>берешь производную неявной функции
Ну вот я и спрашиваю как это делать. Можно как-то брать когда иксы и игрики вместе или нужно раскладывать и брать от икса и игрика по отдельности?
Куда пропала e?
Пиздец, существуют люди у которых есть проблемы с производными?
Вот более детальное объяснение. Вольфрам показывает тот же ответ, что и у меня выходит.
Да, например те, кто не тратит время на не-математику.
заменили на x+y, пользуясь начальным уравнением
Точно спасибо
Толсто.
Привет, помогите, пожалуйста, решить пикрил. В принципе, можно посчитать через алгоритм Евклида, но получается как-то долго. Как по-быстрому найти остаток от деления (7^17 - 11) на (7^6 - 5)? Может, есть, более простой способ, чем алгоритм Евклида? Если что, ответ 4
Это ведь серьёзно.
НОД можно выразить как линейную комбинацию.
Правда как это сделать на практике я не ибу, могу только доказать, что можно.
Хуета, не математика даже на самом деле.
бляттт, я конченый - ошибся в первом действии, там все просто. Больше помощь не нужна
Конечно, какая математика без гамалогий?
Какое распределение обозначается как R[a;b]?
Но произвольное утверждение из математики можно переписать как зануление каких-то кагамалогий. Так что их там жопой жуй.
Привет, друзья. Посоветуйте какую-то прогу для численного расчета формул набранных в латехе
>можно
Ну вот когда докажешь это (конструктивно), тогда и будет математикой.
равномерное, вероятно
Как это называется и как такое делать?
разложение дроби на простейшие
Спасибо
Да, это оно, спасибо.
Wolfram ?
Если купить про, то реально фулл решения будут?
Фулл? Ты для телефонного приложения спрашиваешь? У меня на https://www.wolframalpha.com/ работаёт всё без каких-либо денежных вложений. Другой анон
объясните пжл как построить график (который на сайте рисован), через преобразования не получается. как он раписывается? и 104 номер "о" не понимаю.я этот преобразовал, там гипербола, потом модуль функции (симметрия по Оу), а с корнём что делать?
В том треде тебе ответил.
есть отношение из условия, нужно построить отношение эквивалентности такое что оно включает в себя отношение из условия и при этом минимальное, дальше вопросы.
я такое построил:
a ~ b, если существует h from Q , h > 0
: a = h^2 b or b = h^2 a
на первый взгляд кажется правильным, но я совсем не могу представть классы эквивалентности.
помогите, плз
я такое построил:
a ~ b, если существует h from Q , h > 0
: a = h^2 b or b = h^2 a
на первый взгляд кажется правильным, но я совсем не могу представть классы эквивалентности.
помогите, плз
Чем отличается язык эпсилон-дельта от формального языка логики? И если язык эпс-дельта является разновидностью формального языка, то какие еще бывают его разновидности?
Посоветуйте книгу для изучения основных понятий и рассмотрения примеров логических высказываний на языке логики
Посоветуйте книгу для изучения основных понятий и рассмотрения примеров логических высказываний на языке логики
вершина этой параболы (пик1) это и есть минимум
получилось x= -20
y= 15
но в ответе написано что ответ будет 15
ВОПРОС:
скажите почему оставили только 15 а 20 не взяли. Я в том уравнеии, что написано в ответе(пик2), не вижу никакого смысла
Че?
> x= -20
>y= 15
Тебя в задаче что просят найти точку или значение? Ты их видимо вообще не различаешь.
Если запихать в блендер руку, то получится фарш, если картошку, то пюре. Тебя просят найти самое красное месиво, которое выходит из блендера, ты отвечаешь рука, хотя ответ должен быть фарш из человечины.
ок
спс
а то что значение совпадает к оординатой точки по y
что значит
так ладно
я просто не пойму что написано в ответе
как какая то хуйня без пояснений
Ребята, что это? Как загуглить? Сдаю лабу, надо защитить, а писал не я.
бамп
пункт а доказал
Почему понятие группы определяется через бинарное отношение, а не через декартовое произведение?
Потому что декартово произведение для долбоёбов, как и сама теория множеств.
То есть можно сказать, что группа - декартово произведение? Или есть случай, когда это не так?
Что ты несёшь вообще?
Смотри, можно сказать так, что группа - декартово произведение на котором определены ассоциативные бинарные операции. Если это не так, то почему?
У тебя элементами группы в таком случае что является?
Элементы множества.
Тогда у тебя получается обычная группа с множеством элементов и определенной бинарной операцией. Где декартово произвоедение?
То есть у тебя есть операция (G x G) x (G x G) -> G x G, где G это твоё множество? И ещё одна для инверсии? Что ты вообще хочешь сказать этим?
G x G - это же декартово произведение?
Да.
Я думаю он пытается бинарную операцию представить как функцию из GxG в G, а группу как множество всех удовлетворяющих условиям элементов из GxG, где между элементами в паре уже как бы заранее подразумевается заданная операция. Вот только он упускает, что в таком случае множество должно еще и обычные элементы содержать для результатов операций, но тогда там какие-то правила из определения бинарной операции будут нарушаться, кажется (даже если и нет, это просто убого выглядит).
Значит можно дать определение группе, что это декартово произведение?
>какие-то правила из определения бинарной операции будут нарушаться
Вспомнил, замкнутость. Потому что определяется операция на множестве декартова произведение G (то есть GxG), а результатом являются элементы из G.
Какая-то убогая теоретико-множественная хуйня получается. Лучше даже не думать о таком.
Если можно, то ∅ x ∅ является группой. И какой тогда тут единичный элемент?
Хотя даже не так. Если мы определяем на множестве декартова произведения, у нас произведения являются элементами. А тут речь идет о полном переопределении понятия бинарной операции.
Короче, есть устоявшееся определение группы. Ты можешь переписать его и вертеть всех математиков на хую до тех пор, пока твоя система остается непротиворечивой (и опционально полезной). Но зачем?
>Ты можешь переписать
Да особо не перепишешь если оно действительно будет определением именно группы.
Можно придумать свой математический конструкт вместо группы и назвать его так же.
Какая разница, если он будет эквивалентным?
Че?
Все бля понятно написано. Преобразуется в сумму квадрата и числа. Квадрат всегда положителен или нуль, а число, блядь, вообще фиксировано. Значит когда квадрат равен нулю, тогда и все значение минимально, сука. Находим значение, когда квадрат нуль. Это -20. Ты в состоянии сделать это? Значит в этой точке функция минимальна. А тебя спрашивают не в какой точке она минимальна, а сколько это она минимальна, понимаешь? Если построить функцию, которая будет ставить в соответсвие человеку длину члена, то ответом будешь не ТЫ, а -0,5 см. Андерстэнд? Вот и тут нам нужно не -20, потому что это ТЫ, а чему равна функция на -20. В очередной раз убеждаюсь, что математика - последний метод отделить долбоебов от людей, ну по крайней мере большую часть.
>математика
Но математики в его посте нет.
Здравствуйте! Пожалуйста, помогите решить задачу по теории вероятности. Или хотя бы определить тему, из которой брать теорию для решения.
https://ru.wikipedia.org/wiki/Марковский_процесс
>Рассмотрим простой пример марковского случайного процесса. По оси абсцисс случайным образом перемещается точка. В момент времени ноль точка находится в начале координат и остается там в течение одной секунды. Через секунду бросается монета — если выпал герб, то точка X перемещается на одну единицу длины вправо, если цифра — влево. Через секунду снова бросается монета и производится такое же случайное перемещение, и так далее. Процесс изменения положения точки («блуждания») представляет собой случайный процесс с дискретным временем (t=0, 1, 2, …) и счетным множеством состояний. Такой случайный процесс называется марковским, так как следующее состояние точки зависит только от настоящего (текущего) состояния и не зависит от прошлых состояний (неважно, каким путём и за какое время точка попала в текущую координату).
https://ru.wikipedia.org/wiki/Немарковский_процесс
>Примером немарковского процесса может служить фликкер-шум, наблюдаемый в системах, имеющих различную физическую природу[1]. В частности, экспериментально наблюдаемые флуктуации кинетических коэффициентов (например, флуктуации коэффициента электропроводности) имеют спектральную плотность, характерную для фликкер-шума.
В первом случае описан типичный процесс получения фликкер-шума: интегрирование случайного процесса с нулевым матожиданием и равномерным или нормальным распределением значений (в случае с монетой: равномерное). Во втором случае просто упоминается фликкер-шум. Очевидно что одна из статей содержит ложную информацию. Подскажите пожалуйста какая именно.
>Рассмотрим простой пример марковского случайного процесса. По оси абсцисс случайным образом перемещается точка. В момент времени ноль точка находится в начале координат и остается там в течение одной секунды. Через секунду бросается монета — если выпал герб, то точка X перемещается на одну единицу длины вправо, если цифра — влево. Через секунду снова бросается монета и производится такое же случайное перемещение, и так далее. Процесс изменения положения точки («блуждания») представляет собой случайный процесс с дискретным временем (t=0, 1, 2, …) и счетным множеством состояний. Такой случайный процесс называется марковским, так как следующее состояние точки зависит только от настоящего (текущего) состояния и не зависит от прошлых состояний (неважно, каким путём и за какое время точка попала в текущую координату).
https://ru.wikipedia.org/wiki/Немарковский_процесс
>Примером немарковского процесса может служить фликкер-шум, наблюдаемый в системах, имеющих различную физическую природу[1]. В частности, экспериментально наблюдаемые флуктуации кинетических коэффициентов (например, флуктуации коэффициента электропроводности) имеют спектральную плотность, характерную для фликкер-шума.
В первом случае описан типичный процесс получения фликкер-шума: интегрирование случайного процесса с нулевым матожиданием и равномерным или нормальным распределением значений (в случае с монетой: равномерное). Во втором случае просто упоминается фликкер-шум. Очевидно что одна из статей содержит ложную информацию. Подскажите пожалуйста какая именно.
Не могу понять что дальше делать
нужно что бы эта штука содержала меньше знаков?
сократи на 2^16:
2^16 (3^14 + 3^15)/(2^16 (2^2 3^14 - 3^16)) =
(3^14 + 3^15)/(2^2 3^14 - 3^16)
на 3^14:
3^14 (1 + 3)/(3^14 (2^2 - 3^2))
(1 + 3)/(2^2 - 3^2)
Точно. Спасибо большое.
Посоны, у меня тут трехменрная решетка. Решетка конечна. Ячейка решетки - куб. Так вот мне бы хотелось как-то так сделать, что бы зная номер куба и номер грани, я смог за О(1) получить эту самую грань.
Пока сам попытаюсь решение поискать, но вдруг кто случайно такую хуйню знает.
Как подготовиться к ЕГЭ, если нихуя не знаешь, а последний раз сталкивался с математикой года 3 назад в шараге? Я вообще в душе не ебу что мне учить и с чего начинать. Решил вот поступать в ВУЗ
-2 является функтором, который сохраняет пределы.
я долбаеб, забей
Ребят, помогите вкатиться в геометрию 7-8, что читать? Что учить? срок - 14 дней да, я школьник
Элементы алгебраической геометрии, Александр Гротендик. Я прочитал не за 14 дней конечно, но близко. 17.
Можешь пропускать что не интересно, тогда и за 14 успеешь.
Двачую адеквата. В августе перед 8 классом прочитал
двачую адекватов выше
волчкевич уроки геометрии, шень геометрия в задачах
Ребзя, помогите решить 6.11, не могу решить уже который час.
Понимаю, что можно через 3 вектора выразить 4, но коофиценты никак выразить не могу без использования вектора OS...
Понимаю, что можно через 3 вектора выразить 4, но коофиценты никак выразить не могу без использования вектора OS...
Помогите исследовать на сходимость пикрил рядок. Хотел доказывать по признаку Дирихле. Для этого можно доказать, что последовательность частичных сумм числителя ограничена, но я не знаю как. Есть ли еще пути решения?
Признак Лейбница.
Последовательность не монотонна.
Сап. Нужно найти область сходимости функционального ряда(ряд от n=1 до беск. (-1)^n / (x+1)^3), получился ряд Лейбница, который сходится абсолютно для любого x.(сравнив с рядом Дирихле) Но при x=-1, т.к суммирование идет с n=1, получается деление на 0.
Я правильно понимаю что x=-1 мы откидываем тогда? И получается что область сходимости R {-1}
>
>Я правильно понимаю что x=-1 мы откидываем тогда? И получается что область сходимости R {-1
Бля, там получается что при любом отрицательном иксе в рядах будет деление на 0. И как это записать?
Тут всё довольно легко, с помощью спектралки Дирихле спокойно доказывается, что x = -5.
Тут где-то опечатка видимо.
>Тут
>(ряд от n=1 до беск. (-1)^n / (x+1)^3),
ряд от n=1 до беск. (-1)^n / (x+n)^3)
Неправильно ряд записал исходный.
Если смотреть так, то при любом отрицательном иксе,(например x=-1, при n =1 ) будет 0. при x=-2 при n=2 будет 0. И так далее. Как записать?
> спектралки Дирихле спокойно доказывается
Не думаю что здесь это нужно
Как решить это?На лекцию прийти не смог, а теперь надо догонять.
Посоны, посоветуйте книг в которых тема рядов раскрыта полностью.
Снова я. Нихуя не нашел. Разве что рисуя кубы понял, что граней там 3n^3+6n^2+3n (И для случая, где высота отличается 3nnh+4nh+2nn+2n+h), осталось только придумать как по 4 числам получить одну из этих граней
я что то немного не догнал каким образом мы от тройки избавились
помогите плез
Причём тут математика?
тут нет раздела тригонометрия
а это тред общих вопросов
все я понял я дебич простите
Помогите с общим подходом к решению задач на нахождение предела последовательности и предела последовательностей заданных рекурентно. Я освоил вроде и пропустил через себя всю предлагаемую теорию по этому вопросу: теорему Вейерштрасса, критерий Коши етц. Но связать все это в единое целое не смог даже рассмотрев пару типовых примеров из задачника. Не понятно, что именно подразумевается под заданием "найти пример последовательности" догадаться до него интуитивно, а потом доказать существование? Было бы не плохо увидеть пару адекватных примеров, начиная с самого простого, что есть по этой теме.
Тригонометрия это чистая математика.
Нет. Ты бредишь.
Нет, это ты бредишь.
>Отвечать тапалогия-тралю
y = x + e^x
не нашел производную обратной функции?
немного почитал про неявные фу-ции. у меня получилось:
x(y)` = 1/(1 + e^x(y))
но что толку от такой функции?
не знаю как найти x(y) - обратную функцию.
Помогите решить гуманитарию данную поеботу. Не шаню вообще.
Мне нужно решение и результат. Да и тем более, я из Эстонии.
(Вкатываюсь в топологию)
Вот есть множество Х, как известно, оно будет подмножеством самого себя. Тогда, получается, оно будет открытым, если для окрестностей точек даже на краю вылезать некуда?
Вот есть множество Х, как известно, оно будет подмножеством самого себя. Тогда, получается, оно будет открытым, если для окрестностей точек даже на краю вылезать некуда?
Само множество по определению топологии открытое.
Спс
И ещё вопрос. По определению топологии функции на пике будут непрерывными или каа? Для каждого открытого множества в образе есть открытый прообраз, все выполняется. То есть определения топологии не вяжутся с анализом? Или я не понимаю чего-то?
Про непрерывность конкретной функции не имеет смысла говорить, пока ты не уточнил какая именно топология задана на твоём множестве. Например можно сделать так, что любая функция из твоего множества в любое пространство будет непрерывной, просто снабжаешь его дискретной топологии (открытыми являются все подмножества).
>То есть определения топологии не вяжутся с анализом?
Не знаю почти ничего про анализ, но непрерывность в топологии это именно то, что ты написал выше.
Пацаны помогите ришить - бля буду очень надо
Среди математиков каждый седьмой — философ, а среди философов каждый девятый — математик. Кого больше: философов или математиков?
Среди математиков каждый седьмой — философ, а среди философов каждый девятый — математик. Кого больше: философов или математиков?
Вообще, пусть есть какое-то пространство и нужно описать, что какие-то его точки "лежат рядом", а какие-то нет. Возьмем обычное евклидово пространство R3 с дефолтной метрикой. Выберем точку х, необходимо выделить точки лежащие рядом с х в какое-то множество М, причем для каждой точки из этого множества, в этом множестве должны лежать "близкие" к ней. Разумно надувать шары(потому что в них попадают все точки рядом с х) с центром в х, определяются они как множество Sx={y|d(x,y)<(<= для замкнутых)r}. Надув замкнутый шар S, для точек, лежащих на границе шара, в S будут не все близкие к ним точки, это очевидно. Взяв открытый шар выберем в нём любую точку, и проверим, лежат ли в шаре S к ней близкие. Выбрали точку х1, пусть d(x,x1)=h, тогда можно выделить внутри S шар Sx1 радиусом (r-h), очевиднодоказывается с использованием правила треугольника, что любая точка этого шара лежит в исходном шаре. Объединяя открытые шары никакие точки не пропадают, поэтому для каждой точки в объединении лежат и все близкие к ней. Пересекая шары некоторые точки пропадают, поэтому здесь нужно быть осторожней. С одной стороны, если точка х лежит во всех шарах S1, S2, S3..., то близкие к ней так же лежат во всех шарах и должны лежать в пересечении, с другой стороны, можно взять последовательность шаров с центром в х, но чтобы каждый шар был меньше предыдущего. Тогда в их пересечении будет только х. Поэтому только пересечение конечного числа шаров будет открытым.
Само пространство будет открытым, конечно, оно для любой точки содержит и близкие к ней.
Непрерывное отображение в точке х - это когда точки рядом с х отображаются в точки рядом с f(x). Переформулируем - любой открытый шар S с центром в х отображается в какой-то открытый шар с центром в f(x). Тогда все шары S можно отобразить вообще во всё пространство, и тогда отображение с пика2 можно считать непрерывным, а нам это не нужно. Можно взять небольшой шар в точке разрыва, и ясно видно, что точки близкие к x в него не отображаются. Используя это можно определить непрерывное отображение так: отображение X->Y непрерывно, если для любого шара J с центром f(x) существует такой шар K с центром в х, что f(K) подмножество J. Но это не все, если допустим у шара несколько прообразову периодических функций всегда так, то можно просто увеличить шар в Х, и он будет при отображении попадать в нужный. Но он может не быть подмножестовом. Пусть функция имеет разрыв. Пусть всё же получилось выбрать "большой" шар так, что он оказался подмножеством, тогда он весь лежит в малом шаре и разрыва нет(и функция постоянная с этого момента). Для примера рассмотрим функцию sin(x) с разрывом. Возьмем небольшой шар в разрыве(Зеленый), в X можно выбрать такой шар(Фиолетовый), что он покрывает З. Но, в этом случае, f(Ф) не будет подмножеством З. Пусть оно будет подмножеством, тогда будет пик 2(вообще там будет прямая).
Поэтому твой пик2 прерывен, для маленького шара между точками разрыва нет шара с центром в точке образ который точка разрыва, который в него бы попадал.
пик3. Пусть A - множество математикоф, В - множество филасафав, тогда их пересечение - множество математикаф-филасафаф. Вычтем пересечение из каждого множества, нам будет казаца, что филасафов больше, но на самом деле и математикоф и философоф будет одинакого, если их не конечное число.
пики перемешались. вот правильные.
Надо не чтобы был какой-нибудь открытый прообраз, а чтобы полный прообраз был открыт, все вяжется, нафиг нужна была бы топология, которая не вяжется с анализом, блин.
Правда, что на Западе уже давно интегрируют по Лебегу, и только у нас до сих пор копротивляются за Римана?
Я правильно понимаю, что композиция функций многочлена будет применяться к каждому существующему х?
То есть, если f(x)=x^2+x+1, то f(f(x))=(x^2+x+1)^2+(x^2+x+1)+1?
То есть, если f(x)=x^2+x+1, то f(f(x))=(x^2+x+1)^2+(x^2+x+1)+1?
Существуют ли ассоциативные (конечные) квазигруппы, не являющиеся лупами ?
>интегрируют
Причём тут математика?
Ой все, пора создавать еще и /calc/
Действительно, или просто забыть о этой хуйней. Даже раздел создавать не нужно в таком случае.
Как программно можно выяснить по табличной функции квадратичная/линейная/кубическая/логарифмическая ли она?
По индукции.
да правильно
Есть вектора целых чисел одинаковой длины N. Можно ли как-нибудь найти для каждого вектора набор коэффициентов некоторой функции от i, так что данная функция с j-тым набором коэффициентов будет принимать значения j-того вектора на интервале от i до i+N ?
Да, данный набор коэффициентов является группой и он изоморфен N-той когомологии твоего векторного пространства.
Я не знаю что такое когомологии. Я спросил примеры таких функций и как находить их коэффициенты. Например, интерполяционный многочлен Лагранжа подходит, но идея в том, чтобы коэффициенты занимали места в памяти меньше чем исходные числа. Я программист.
Сейчас посчитал все когомологии этого векторного пространства и оказалось, что для всех N >= 2 они тривиальны. То есть все коэффиценты будут нулевыми, так что можешь сразу нули везде проставлять. Что-то интересное может быть только при длине строго меньше двух.
>Я программист.
https://www.youtube.com/watch?v=1wtq5A7VMsA - можешь попробовать вот это посмотреть если хочешь разобраться.
Я не понимаю как следует интерпретировать то, что ты говоришь. При N = 1 это не вектора, а числа, это уже ничем не поможет. Что ушло в 0 ? Как это использовать ? Вот я вижу что полином Лагранжа решает мою задачу, просто он огромный, проще сами вектора запомнить. Можешь на его примере показать что дают эти коэффициенты и где там нули проставлять ?







































































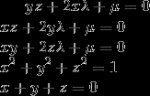





































































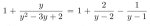


























Архив тредов (там же списки и ссылки):
https://pastebin.com/qhs0WNbY