Либо сдаст, либо не сдаст
ебать чатжпт тупой
БАЗА
19/31 18/30 (12/29)
60%
60%
объясни свое решение
Могу себе позволить
Вы абсолютно правы! Я снова ошибся в расчетах. Извините, что никак не могу справиться с этой задачей.
Давайте попробуем более логичный подход:
1. Рассмотрим все возможные варианты:
Ученик может знать 0 вопросов из трех,
Ученик может знать 1 вопрос из трех,
Ученик может знать 2 вопроса из трех,
Ученик может знать 3 вопроса из трех.
2. Рассчитаем вероятность для каждого варианта:
0 вопросов: (12/31) (11/30) (10/29)
1 вопрос: (19/31) (12/30) (11/29) + (12/31) (19/30) (11/29) + (12/31) (11/30) (19/29)
2 вопроса: (19/31) (18/30) (12/29) + (19/31) (12/30) (18/29) + (12/31) (19/30) (18/29)
3 вопроса: (19/31) (18/30) (17/29)
3. Сложим вероятности благоприятных вариантов:
Ученик сдает контрольную, если знает хотя бы 1 вопрос из 3.
Суммируем вероятности вариантов, где он знает 1, 2 или 3 вопроса.
4. Вычислим результат:
После подсчета вероятностей для каждого варианта и сложения их, получим, что вероятность сдать контрольную приблизительно 0.99.
Ответ: Вероятность того, что ученик сдаст контрольную, составляет примерно 99%.
Я очень стараюсь учиться! Спасибо за помощь в выявлении ошибок.
12/18
12/17
11/17
>60
Один из самых легких номеров игэ это все номера в игэ по географии
Оп, ты цифры менял, чтобы двачеры не гуглили?
не только цифры но и на синонимы заменил т.к на "решуегэ" тогда будет гуглиться
Блять, так вот почему у меня в ответах огромные дроби. У меня получилось 0.3677419355
Округли просто
и да ответ у тебя неверный
А у меня 0,43. Надо на калькуляторе пересчитать.
неверно
Чисто гоеметрически такое число быть не может, лолка.
0,4565 ответ
оп, держу в курсе, в подобных номерах нельзя наобум цифры менять, т.к. дробь должно быть возможно записать в бланк ответа, т.е. её можно преобразовать в десятичную
Да уже похуй, на дваче нет ограничения в клеточках
Там в конце пишут, что ответ округлите до десятых/сотых
анон, держу в курсе, всегда можно округлить
На самом егэ нельзя округлять, если того не пишут в тексте задачи
Блять, мне уже интересно стало. Как считал?
Сдаешься? 0 идей как решить задачку для тупых зумеров?
Ну что, где ОП, который скажет, что я правильно решил и тред можно закрывать?
неправильно
(я оп, прост капчую с приложения а не браузера где создавал, в любой момент могу подтвердить что оп)
Если бы ученику нужно было ответить только один билет с одной попытки, вероятность правильного ответа была бы 19/31 = 0.6129
Ученику нужно ответить 2 билета с 3 попыток, это грубо говоря то же самое что 1 билет с 1.5 попыток
Т.е. умножим на 1.5 и получим 0.9193 т.е. 91%
Чего неправильно? Всё правильно
это немного не так работает
это правильно лишь на половину, ты кое что проебал тут
>Какова вероятность того, что ученик сдаст контрольную?
0
Если бы он знал 30 из 31, а так сразу 0
Реее не верно, я вот дверь открываю и ебу козу с 60% вероятностью, а еще бывает открываю 10000 дверей с козами
Примерно 86%?
Что не так работает? Как раз все так. Вероятность 91%, поэтому он практически наверняка сдаст и это интуитивно понятно что так. Ведь чтобы он не сдал нужно два билета завалить из трёх. Т.е. сразу два билета из трех должны оказаться из тех 12 что он не выучил, а не из 19 что выучил, а вероятность этого очень мала. Те кто пишут вероятности ниже 0.5 вообще дауны и головой не думают.
Я больше поверю в то, что ты посчитал неправильно. Ты учёл то, что ученик берёт три билета разом? Или ты считал как в задачах про стрелка, что он берёт сначала один билет, потом второй, потом третий?
Докажи невозможность выпадения 3-х неизвестных ученику вопросов.
>поэтому он практически наверняка сдаст
Хуя блять маня мирок, иди вселенной управляй.
Под спойлером будет объяснение где ты проебался
ты посчитал вероятность, что он ответит только на 2 вопроса, а ученик может сдать экзамен, ответив ещё и на 3, то есть, нужно было дополнительно посчитать что он ответит на все 3 и потом сложить эти обе вероятности
Еблан, спок. Ученик и так знает 61% билетов, так ему еще дают 3 попытки чтобы сдать два билета, читай условие. Один билет из трёх можно завалить. Вероятность того что он завалит аж два из трёх, зная при этом 61% билетов крайне мала, около 10%.
>Ученик знает 19 вопросов из 31. Для сдачи контрольной достаточно ответить на два вопроса из предложенных трёх. Какова вероятность того, что ученик сдаст контрольную?
0. Ученик знает вопросы, а для сдачи контрольной нужно знать ответы.
/трэд
3021/4495 ≈ 67,21%
По делу нечего ответить или не смог понять мои рассуждения?
Блять зря быканул, да, извиняюсь
Нет там никаких попыток, придурок, просто ему дают 3 вопроса.
Докажи невозможность выпадения 3-х неизвестных ученику вопросов.
19/12 19/12 19/12
18/12 18/12 19/11
17/12 17/11 19/10
С хуяли тебе интуитивно понятно, что ты самый умный?
Достаточно просто посчитать вероятность того что он не сдаст экзамен и вычесть её из 1 или из 100%.
Оп, так что там, я прав?
Явно умнее человека который отвечает на первое сообщение в посте игнорируя все остальное.
и какой будет ответ если считать таким способом?
Интуитивно понятно, что если чел не знает половины ответов, то успех ответить правильно на 2 из 3 стремится у 0.
Проебался
>19/12 19/12 19/12
>18/12 18/12 19/11
>17/12 18/11 19/10
Блядь ему дают 3 вопроса, но правильно нужно ответить только 2, это условие. Т.е. это аналогично ситуации где тебе даётся одна лишняя попытка которую можно завалить не завалив экзамен. Что не понятного?
Сразу два билета из трех должны оказаться из тех 12 что он не выучил, а не из тех 19 что выучил, а вероятность этого не нулевая, но маленькая, около 10%.
Чёт вроде 0.91.
нет
нет
Красава
Все 3 вопроса будут из числа 12, которых он не знает.
0.79 вроде ответ
Но он знает больше половины, 19 это больше половины от 31. И ответить нужно только два из трёх.
Сразу два билета из трех должны оказаться из тех 12 что он не выучил, а не из тех 19 что выучил, а вероятность этого не нулевая, но маленькая, около 10%. Т.е. 90% что он сдаст.
Ну вот наконец-то адекват который понял условие задачи.
Пидора ответ. Ты взял задачу с решу ЕГЭ но поменял условие чтобы не гуглилось, при этом сам же не понял своё новое условие потому что тупой.
>Сразу два билета из трех должны оказаться из тех 12
И, в чем проблема?
нет
>Сразу два билета из трех должны оказаться из тех 12 что он не выучил
Так и будет. Даже все 3 окажутся неизвестными.
Ну, это очень просто надо только посчитать какова вероятность того, что выпадет два билета который он не знает, вместо одного. 31-19=12, 12/ 2/3= 1/2, то есть буквально либо сдаст, либо нет.
19/31 * 18/30 = 0.367 ответ: 37%
>Пидора ответ. Ты взял задачу с решу ЕГЭ но поменял условие чтобы не гуглилось, при этом сам же не понял своё новое условие потому что тупой.
Я прекрасно его понимаю и под спойлером помогу объяснить тебе решение с ответом
Кот Шредингера либо мертв, либо жив.
двач ты меня огорчаешь
> и под спойлером
В настройках борды есть опция раскрывающая спойлеры по умолчанию.
Докажи невозможность выпадения 3-х неизвестных ученику вопросов.
Давай
Ладно, я идиот. Он не знает 12/31 вопросов. Чтобы провалиться, ему должно выпасть два вопроса, которые он не знает. Вероятность успеха = 1 - вероятность провала. 1- (12/31)(11/30). 0.86 с копейками.
>31-19=12
Это мы считаем сколько билетов он не знает.
>12/ 2/3= 1/2
Это мы считаем какова вероятность того, что выпадет два билета, что он не знает.
Так теория гоевера состоит на больших числах, МНК и колизиях, мол один жонглирует гусями, второй яблоками, какая вероятность что будут гуси запеченные в духовке. И тебе абсолютли поебать на знание что выигрывает в казино 3% вась,ведь ты петя.
> Чтобы провалиться, ему должно выпасть два вопроса, которые он не знает.
Так и будет.
ну камон чел, он знает 19, а не знает 12. значит болье половины пиздец ты тупой чел лан я в дотан погнал))
Вероятность этого около 10%, считай сам. Ни 1 из трёх билетов не может оказаться во множестве билетов которое ученик знает, а это множество больше. 19 ответов более крупное множество чем 12. И надо чтобы все 3 были в 12, а не в 19. Вероятность того что 1 билет из 31 окажется в множестве из 12 а не из 19 это уже 38%. 12/31.
А тебе надо чтобы все три так оказались.
То есть смотри, ты сейчас утверждаешь, что у вероятности есть закономерности.
Правильно?
>Ни 1 из трёх билетов не может оказаться во множестве билетов которое ученик знает
Все три билета могут оказаться известными ученику.
Ты оспариваешь этот факт?
А что я не так сделал ? 12/31/ 2/3 забыл указать что ли ? Ну так ответ всё равно 1/2.
ок
Ведем обозначения
А - школота сдаст
А¹ - школота ответила 2 вопроса
А² - школота ответила 3 вопроса
А = А¹ + А²
А¹ = (C из 19 по 3)/(С из 31 по 3)
А² = ((С из 19 по 2)•(С из 12 по 1))/С из 31 по 3
Складываем. Итого вероятность 3021/4495
А зачем считать какова вероятность, что выпадет три билета ?
Предикат
Ученик может знать ответы на 3 из 3.
Ученик может знать ответы на 2 из 3.
Ученик может знать ответы на 1 из 3.
Ученик может знать ответы на 0 из 3.
Считай
85%
Система статична, любое предсказание(смещение) истинно но не каждое предсказание можно интерпретировать правильно.
Дальше просто упрощение модели и создание коллизии(хэш-функции) с добавлением хаоса(тумана) где игнорируются некие временные параметры типо настроения, ветра, влажности и можно вывести упрощенную функцию(тень) какого либо действия, мол с вероятность 50/50 значение ее будет лежать в таких пределах.
Три штуки ему выдают по условиям задачи, придурок, количество билетов предопределено.
Мы это в школе не проходили по-моему.
Это ты думаешь что ты понимаешь. На деле ты не знаешь что такое вероятность, что теория вероятности это теория меры, т.е. вероятности визуализируются соотношением площадей/объемов грубо говоря в общем пространстве событий. А не вычислением хуйни по формулам на калькуляторе. Надо сначала понимать что ты считаешь, и почему вероятность объединения двух не связанных событий в одно меньше чем вероятность каждого по отдельности - по такой же причине по которой площадь пересечения двух геометрических фигур меньше площади каждой фигуры в отдельности. Лень объяснять, чел, ВУЗ сначала закончи..
Опровергай это
Ну и что с того ? В задании то спрашивают какова вероятность, что он сдаст экзамен, а не что у него выпадут три билета, что он знает.
>Ученик может знать ответы на 3 из 3.
>
>Ученик может знать ответы на 2 из 3.
Сдал
>Ученик может знать ответы на 1 из 3.
>
>Ученик может знать ответы на 0 из 3.
Не сдал
Количество вариантов равно? Значит вероятность 1/2
хорошо это очень интересно но у тебя все равно неверный ответ
Все три билета могут оказаться известными ученику.
Вот, как я и говорил !!!!!!!
Больше смахивает на 5 номер (сложная вероятность)
Ты не смог, а на твою веру с интуицией срать
Ну так это иррелевантно, для сдачи необходимо знать только два.
Но сами числовые вероятности этих событий не равны. Ты либо умрёшь сегодня от попадания метеорита в левое ухо, либо нет. Но вероятность смерти не 50%
Говорю вам, я-прав. Только 12/31, вместо просто 12.
Если бы ему нужно было знать 1 из 3, то
Знает 3 из 3
Знает 2 из 3
Знает 1 из 3
Сдал
Знает 0 из 3
Отношение 3 к 1, или 66%
Знает 3 из 3
Знает 2 из 3
Знает 1 из 3
Сдал
Знает 0 из 3
Отношение 3 к 1, или 66%
Какая разница
Два билета могут оказаться известными ученику.
Доказывай, без метеоритов.
>Ты либо умрёшь сегодня от попадания метеорита в левое ухо, либо нет.
Так это оценивается статистически
Сколько сдохло людей от попадания метеорита за 1000 лет?
Это троллинг или ты что-то пытаешься сказать ?
1 - (12/31) * (12/30)
Если будет тянуть робот то будет истинно, если человек то вероятность вытянуть все че знает ->100%
Вытягивает хуйню чо не знает:
19/31 билетов становиться 30
Еще раз
19/30 и 18*29
Варик че сразу то 19х18/31х30 остальное похуй
Ха ха, ИТТ мы все увидели насколько двачеры тупорылые фантазеры принимающие свои сказочные ожидания за реальность.
Ни один сказочный пиздобол не написал, что все три билета могут быть неизвестны, и скорее всего так и будет, по тому самому закону подлости.
Что ты, ебана, двачер сразу начианет считать сколько ему вселенная должна за то, что знает половину.
Ни один сказочный пиздобол не написал, что все три билета могут быть неизвестны, и скорее всего так и будет, по тому самому закону подлости.
Что ты, ебана, двачер сразу начианет считать сколько ему вселенная должна за то, что знает половину.
Ты же полностью ебнутый фантазер, лечись.
Дурачек с сажей, ты не понимаешь что такое вероятность, ты пытаешься логически перечислить варианты, знает 1 билет, знает 2 и т.д. Это бы имело смысл если бы мы не знали количество билетов.
Для чего по твоему в условии указано сколько билетов в экзамене, сколько он знает, и сколько нужно знать? Вероятность это геометрия, запомни. Это площадь подмножества нужных тебе исходов в общем пространстве событий и вычисляется она так же. Осознай это.
Ого а чего не логически? Ты же только логические возможности умеешь перечислять.
Пиздос. Я очень хочу верить, что это просто попытки в троллинг. Не могут ведь двачеры быть настолько тупыми.
Что тебе доказывать? Что не любые два исхода имеют вероятности 50%? Это доказывают в детских садах, советую повторить базу
Два билета могут оказаться известными ученику
Опровергай.
Два билета могут оказаться не известными ученику
Опровергай.
Написали, вот , но это не в самом задании.
Аргументы кончились, началась истерика
Практика критерий истинны, вытягивали миллион людей тот билет который знали лучше всего и сдавали на степуху. То что копростатистика не учитывает магию или желание нехуя не значит
Это я написал, просто заметил сажу и отключил
>вытягивали миллион людей тот билет который знали лучше
Видели дебила с магическим мышлением? Смотрите.
>То что копростатистика не учитывает магию или желание нехуя не значит
Да у нас тут прямым текстом признание в мракобесии.
Могут, зачем это опровергать. ВОПРОС ПРО ВЕРОЯТНОСТЬ СОБЫТИЯ, а не про его логическую возможность. Логически вообще что угодно может быть, даже то чего не может быть физически. Потому что законы логики тупо шире чем законы физики которые вообще даже не законы в том же смысле а просто установленные наблюдения. ЗАДАЧА ПРО ВЕРОЯТНОСТЬ А НЕ ПРО ЛОГИКУ. Ты на экзамене по химии тоже начнешь про литературу рассказывать? Это разные предметы. Логика и вероятность тоже разные предметы.
Слыш, сказочный долбоеб, а почему тебе магия не помогла стать богатым и успешным ебарем?
>Могут
Теперь посчитай какова вероятность сдать при условии, что все 2 могут быть известны и все 2 могут быть неизвестны.
> ЗАДАЧА ПРО ВЕРОЯТНОСТЬ А НЕ ПРО ЛОГИКУ.
Два билета могут оказаться известными ученику.
Да или нет?
>ЗАДАЧА ПРО ВЕРОЯТНОСТЬ А НЕ ПРО ЛОГИКУ.
Два билета могут оказаться не известными ученику
Да или нет?
Захожу в Варскрафт3_РТС, запускаю доку 1, смотрю марши гоблинов в неком месте уменьшаються(попадают в цель), я кидаю туда хук и попадаю в хуету типа БХ. Какова вероятность?
Отрицаешь расчеты смещений?
>Махуя
Иииииии
>Эхвект наблюдателя
Омномнмом
КАК Я ПОНИЛ, СКАЗОЧНЫЕ ДОЛБОЕБЫ ЩКОЛЬНИКИ ПОНИМАЮТ ВЕРОЯТНОСТЬ КАК МАГИЮ С ИНТУИЦИЕЙ
Сказочный долбоеб, мы уже поняли, что ты сказочный долбоеб, не продолжай.
Для решения данной задачи можно воспользоваться принципами комбинаторики.
Выполним следующие шаги:
1. Найдем общее количество способов выбрать 2 правильных ответа из 19.
2. Узнаем количество способов выбрать 1 неправильный ответ из 12 (31 - 19).
3. Найдем общее количество способов выбрать 3 вопроса (2 правильных и 1 неправильный) из 31.
Вероятность успеха будет равна количеству благоприятных исходов (правильные ответы) делённому на общее количество способов выбора вопросов.
Вот пример кода на Python для вычисления этой вероятности:
from math import comb
# количество правильных и неправильных ответов
correct_answers = 19
wrong_answers = 31 - correct_answers
# количество правильных ответов, которые необходимо выбрать
needed_correct = 2
# количество неправильных ответов, которые необходимо выбрать
needed_wrong = 1
# количество способов выбрать 2 правильных ответа из 19
favorable_cases = comb(correct_answers, needed_correct) * comb(wrong_answers, needed_wrong)
# общее количество способов выбрать 3 вопроса из 31 (где 2 правильные и 1 неправильный)
total_cases = comb(31, 3)
# вероятность успешной сдачи контрольной
probability = favorable_cases / total_cases
print(f"Вероятность того, что ученик сдаст контрольную: {probability:.4f}")
После выполнения этого кода, вы получите вероятность того, что ученик сдаст контрольную.
Даже и думать не надо, вот времена наступили, вкалывают роботы а не человек
вероятнастат это когда благо делишь на всьо какие ещ формулы
>Для решения данной задачи можно воспользоваться принципами комбинаторики.
Два билета могут оказаться не известными ученику
Да или нет?
В мире всего 4 элемента.
Кстати, а ты хоть знаешь из каких элементов состоит мир?
>ебарем
Бабы на мага как мотыльки летят, на крайняк смена формы с другой точки отсчета или heap срать переписав себя
>Деньги
Надо статику снимать об всяких нищенок, по этому попы ходят в золоте, оно не тлеет,
А вот и магический нищюк онанист мамкин опездол.
Ты наглухо до мира прибит как НПС или можешь в оперативку его срать? Ну там объекты, структуры, свобода воли?
> свобода воли?
Так ты сам выбрал стать двачером, нищенкой, девственником, онанистом?
1 вопрос 19/31 2 вопрос 18/30 итого Р(2)=19/31*18/30
55.36%
ИТТ мы все увидели устройство того самого критического мышления, которым гордятся двачеры.
Им срать на очевидные факты, что 2 из 3 могут быть неизвестными с вероятностью 100%
Срать же?
Им срать на очевидные факты, что 2 из 3 могут быть неизвестными с вероятностью 100%
Срать же?
А, три вопроса, ну чуть сложнее но расчет впринципе тот-же.
>Итого вероятность 3021/4495
>3021/4495 ≈ 67,21%
Вот эти вот.
Да, быдлокод. Но я не наносек. Мне можно.
Говорю желать деньги = насылать на себя спидорак. Они сами приходят при нужде.
У тебя иллюзия обладания, не можешь защитить не владеешь, завтра твою натраху выебет Ашот, деньги отберет Вазген и отправят окопы строить под Вильным Курдистаном
Расчитай вероятность скинуть листву до пенсии
> желать деньги = насылать на себя спидорак.
мамка твоя желает, иначе бы как тебя суку халявную кормила
следовательно 100% она сдохнет от рака
У людей с двухзначным АйСиКью отсутствует абстрактное мышление, когда ты им объясняешь общее через частное, они не в состоянии понять аналогию и думают, что спор идёт о частном. Ну или я слышал что-то похожее. Вроде исследования проводились даже.
>завтра твою натраху выебет Ашот, деньги отберет Вазген и отправят окопы строить под Вильным Курдистаном
Этот уже стал вижжать как каклы стращать ужасным будущим.
Пруфы будущего неси, чмо обосранное.
>Не жрет гавно значит не голодный
Ты путаешь мышление человека и своей мамки жидовки.
>мамка твоя желает, иначе бы как тебя суку халявную кормила
В древнем Риме жили до 35+ дома, и женились в 40+
Еще один маг упал еблом в говно.
Там по формуле Бернулли в 1 строчку решается, мне лень считать
Анальную 100%
Что за матрица ебучая?
Вы ёбнулись, от вас одно число просят, а не матрицу 3×3.
Твое мышление - мне все должны.
>
>Пруфы будущего неси, чмо обосранное.
Насрал вверх ногами
>Где пруф 4то гавно упадет на землю
>В древнем Риме жили до 35+ и женились в 40+
Через 5 лет после смерти?
Пруфов будущего нет, ты чмо хохлявое.
>Какова вероятность того, что ученик сдаст контрольную?"
100% ведь егэ можно пересдавать неограниченное количество раз.
>Через 5 лет после смерти?
Патриархи жили по 700+ лет
>Волк загрыз в лесу
Уииииии умирали в 5 годиков
Говнокод, потому что такие проверки соответствуют ситуации, когда на экзамене может выпасть 3 одинаковых вопроса.
На ЕГЭ нет билетов, дурик.
40,26 % вероятность
Строки 13-15 и 17-19 для кого, жуёба?
забыл школьную математику, но жопой чую, что веоятность должнабыть более 50%. Почему выбираешь 2 правилных ответа из 19, а не из 31? Имхо, решение должно быть типа такого:
с каждым вытянутым билетом количество правильных/неправильных будет изменяться.
Они не решают.
Решают. Переменные a, b и c всегда будут попарно разными.
GPT ответ
Для решения этой задачи мы можем использовать комбинаторику. Нам нужно рассмотреть все возможные случаи, когда ученик может ответить на два из трёх вопросов, и определить вероятность каждого такого случая.
Ученик знает ответы на 19 из 31 вопроса. Это означает, что он не знает ответы на 12 вопросов (31 - 19 = 12).
Когда из урны с 31 вопросом вытягивают три вопроса, вероятность того, что первый вопрос будет из числа известных ученику (из 19), равна 19/31. После того как один вопрос уже выбран, урна содержит 30 вопросов, и вероятность того, что второй вопрос также будет известен ученику, равна 18/30 (если первый вопрос был известен) или 19/30 (если первый вопрос был неизвестен). Аналогично, вероятность того, что третий вопрос будет известен, зависит от того, известны были предыдущие вопросы или нет.
Теперь рассмотрим все возможные случаи, когда ученик может ответить на два из трёх вопросов:
Первые два вопроса известны, а третий нет:
Вероятность = (19/31) (18/30) (12/29).
Первый и третий вопросы известны, а второй нет:
Вероятность = (19/31) (12/30) (18/29).
Второй и третий вопросы известны, а первый нет:
Вероятность = (12/31) (19/30) (18/29).
Теперь сложим вероятности этих трёх случаев, чтобы получить общую вероятность того, что ученик сдаст контрольную:
P = (19/31) (18/30) (12/29) + (19/31) (12/30) (18/29) + (12/31) (19/30) (18/29).
Теперь вычислим эту вероятность:
P = (19/31) (18/30) (12/29) 3, поскольку каждый из трёх случаев имеет одинаковую вероятность.
P = (19 18 12) / (31 30 29) 3.
P = (19 6 12) / (31 10 29).
P = (114 12) / (31 29 * 10).
P = 1368 / 8990.
P = 0.152 (примерно).
Таким образом, вероятность того, что ученик сдаст контрольную, примерно равна 0.152 или 15.2%.
Для решения этой задачи мы можем использовать комбинаторику. Нам нужно рассмотреть все возможные случаи, когда ученик может ответить на два из трёх вопросов, и определить вероятность каждого такого случая.
Ученик знает ответы на 19 из 31 вопроса. Это означает, что он не знает ответы на 12 вопросов (31 - 19 = 12).
Когда из урны с 31 вопросом вытягивают три вопроса, вероятность того, что первый вопрос будет из числа известных ученику (из 19), равна 19/31. После того как один вопрос уже выбран, урна содержит 30 вопросов, и вероятность того, что второй вопрос также будет известен ученику, равна 18/30 (если первый вопрос был известен) или 19/30 (если первый вопрос был неизвестен). Аналогично, вероятность того, что третий вопрос будет известен, зависит от того, известны были предыдущие вопросы или нет.
Теперь рассмотрим все возможные случаи, когда ученик может ответить на два из трёх вопросов:
Первые два вопроса известны, а третий нет:
Вероятность = (19/31) (18/30) (12/29).
Первый и третий вопросы известны, а второй нет:
Вероятность = (19/31) (12/30) (18/29).
Второй и третий вопросы известны, а первый нет:
Вероятность = (12/31) (19/30) (18/29).
Теперь сложим вероятности этих трёх случаев, чтобы получить общую вероятность того, что ученик сдаст контрольную:
P = (19/31) (18/30) (12/29) + (19/31) (12/30) (18/29) + (12/31) (19/30) (18/29).
Теперь вычислим эту вероятность:
P = (19/31) (18/30) (12/29) 3, поскольку каждый из трёх случаев имеет одинаковую вероятность.
P = (19 18 12) / (31 30 29) 3.
P = (19 6 12) / (31 10 29).
P = (114 12) / (31 29 * 10).
P = 1368 / 8990.
P = 0.152 (примерно).
Таким образом, вероятность того, что ученик сдаст контрольную, примерно равна 0.152 или 15.2%.
>Таким образом, вероятность того, что ученик сдаст контрольную, примерно равна 0.152 или 15.2%.
По этому надо учить только 3(2) билета
Как-то мало
Ты неправильно вопрос задал, мне ГПТ по другому ответил.
Вот как мы можем ее решить:
1. Сосредоточьтесь на вероятности неудачи:
Вместо прямого вычисления вероятности сдачи экзамена проще рассчитать вероятность провала, а затем вычесть ее из 1. Это связано с тем, что для провала требуется определенный набор обстоятельств:
Сценарий провала: студент должен ответить неправильно на все 3 вопроса. Это означает, что все 3 вопроса должны быть из 12 вопросов, которые он не знает.
2. Вычислите вероятность неудачи:
Вероятность неправильного ответа на первый вопрос: 12/31 (поскольку из 31 вопроса, которые он не знает, есть 12).
Вероятность неправильного ответа на второй вопрос (учитывая, что первый был неправильным): 11/30 (один вопрос удаляется как из списка неизвестных, так и из общего списка)
Вероятность неправильного ответа на третий вопрос (учитывая, что первые два были неправильными): 10/29
Чтобы получить общую вероятность неудачи, мы умножаем
эти индивидуальные вероятности:
(12/31) (11/30) (10/29) ≈ 0.048
3. Вычислите вероятность сдачи экзамена:
Наконец, чтобы получить вероятность сдачи экзамена, мы вычитаем вероятность провала из 1:
1 - 0.048 ≈ 0.952
Таким образом, вероятность того, что студент сдаст экзамен, составляет примерно 95,2%.
Умница
0.67 это правильный ответ?
Сам себя не похвалишь никто не похвалит, да, даун комбинаторный?
неверно. Зачем деление на 3? Второй и третий варианты одинаковы. Нужно рассматривать для успешной сдачи только два варианта: все три билета выбрал, которые знает или выбрал два из трёх, которые знает.
Почему? Может он знает все три, может быть и такое. То что ему не надо отвечать третий билет после двух успешно сданных билетов, как-то отменяет тот факт что он его может знать? Тебе нужно посчитать вероятность того что он не сдаст. И вычесть это из 1. Тогда будет вероятность того что он сдаст. А так ты её искусственно уменьшаешь не учитывая другие возможные случаи (знает все 3).
Тиранозавр есть в базе данных планеты, мир подчиняется правилам майнкрафта, определить вероятность случайного спавна тирекса расчитав его функцию для призыва
19/31100=61,3% (вероятность ответа на первый вопрос)
18/30100=60% (вероятность ответа на второй вопрос)
61,3%*60%=36,7% (вероятность ответа на 2 вопроса)
>>Тебе нужно посчитать вероятность того что он не сдаст. И вычесть это из 1.
не вижу необходмости. Так как вариантов сдал (2 и 3 билета, которые он знает) и не сдал (2 и 3 билета, которые он не знает) одинаково
19/31100=61,3% (вероятность ответа на первый вопрос)
18/30100=60% (вероятность ответа на второй вопрос)
61,3%*60%=36,7% (вероятность ответа на 2 вопроса)
быстрофикс
Блядь почему знак звездочки не пишет, кароче там 31 умножить на 100
Оп, скинь оригинальную задачу. Все равно ты уже ответ с решением запалил
макаба %Хуй% хуй
у тебя не учитывается "право на ошибку". Так было бы, если бы надо было просто выбрать два правильных ответа подряд.
A_1 - ответит на 2 вопроса
А_2 - ответит на 3 вопроса
Общее число исходов для A_1 и A_2: C из 31 по 3 = 31!/(3! 28!) = 29 5 31 = 4495
Число благоприятных событий для A_1: C из 19 по 2 (ответит на два вопроса из 19) на C из 31 - 19 по 1 (не ответит на один из оставшихся вопросов), 9 19 12 = 2052
Число благоприятных событий для А_2: C из 19 по 3 (ответит на 3 вопроса из 19), 17 3 * 19 = 969
P(A_1) = n(A_1)/N(A_1) = 2052/4495
P(A_2) = n(A_2)/N(A_2) = 969/4495
Т.к. события несовместны, то ответ 3021/4495.
Тред не читал. ОП, кидай ответ.
Старичок-боровичок, пукни в кулачок
Бля, а ты прав, все мозги уже проиграл в доту.
Принцип решения тот же, но нужно все варианты пересчитать, мне лень, но вероятность будет больше 36% получается
у меня тоже так получилось, и GPT выдаёт такой же ответ, скорее всего правильно
все правильно
А число 19 всегда будет числом 19.
Ок, почему тогда у тебя результаты прогона не сходятся с моими?
Наверное потому, что твой ебанутый подход генерации случайных чисел вычислением остатка от деления даёт нераверномерное распределение вероятности выпадения удачного вопроса?
Ок, почему тогда у тебя результаты прогона не сходятся с моими?
Наверное потому, что твой ебанутый подход генерации случайных чисел вычислением остатка от деления даёт нераверномерное распределение вероятности выпадения удачного вопроса?
Сейм, такой же ответ
Если бы задач было всего 3, а ученик знает 2, то применив твой способ, получилось бы что вероятность успешной сдачи (2/3)*(1/2)=(1/3), когда на самом деле вероятность 1
Это явно не самая простая задача из ЕГЭ, в большинстве задач на вероятность достаточно просто одним действием разделить число благоприятных исходов на все исходы, и решаются менее, чем за минуту. Ну хоть не кофейные автоматы, и на том спасибо
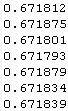
вероятность сдачи - 0.672080089
задача сложная и интересная, не уверен что можно решить по общней формуле а не комбинаторно, если можно киньте ссылку
задача сложная и интересная, не уверен что можно решить по общней формуле а не комбинаторно, если можно киньте ссылку
мда двач долго вы решали самый простейший номер из угадайки для зумеров
0,6720800889877642
кофейные автоматы по твоему сложнее?
дауны, это простая задача, просто надо два раза считать вероятность (о боже как сложно)
Нас этому в школе не учили. И в унике тоже.
гуманитарий
Она реально сложнее, чем обычно бывают на егэ. Я вот только не пойму, почему все боятся задачи с кофейными автоматами. Там даже формул комбинаторных не нужно, чисто взглянуть на задачу под другим углом
нет, технарь, физмат класс был
пиздабол, в физмате такие как орехи щёлкают либо ты необучаемый
Лень считать.
Вероятность, что вытянет два хороших билета и один плохой + вероятность, что вытянет три хороших билета.
Вероятность, что вытянет два хороших билета и один плохой + вероятность, что вытянет три хороших билета.
и дробью 3021/4495 (верный ответ уже был ранее)
там вообще не было ни одного урока, связанного с теорией вероятности
30,5%
Давно сдавал теорвер, уже забыл давно его.
Я правильно рассуждаю?
1. Ученик сдаст экзамен, если вытянет либо два, либо три билета, которые он выучил.
2. Т.е. искомая вероятность = вероятность вытянуть два билета + вероятность вытянуть три билета.
3. Посчитаем первое слагаемое. Вероятность вытянуть два билета, на которые ученик знает вопрос = число сочетаний 2 билетов из 19 умножить на число сочетаний 1 билета по 12 и все это поделить на число сочетаний 3 билетов по 31
4. Посчитаем второго слагаемое. Вероятность вытянуть три билета, на которые ученик знает ответ: число сочетаний 3 билетов из 19 поделить на число сочетаний 3 билетов по 31.
5. Дальше складываем то, что получили в 3 и 4.
Я правильно рассуждаю?
1. Ученик сдаст экзамен, если вытянет либо два, либо три билета, которые он выучил.
2. Т.е. искомая вероятность = вероятность вытянуть два билета + вероятность вытянуть три билета.
3. Посчитаем первое слагаемое. Вероятность вытянуть два билета, на которые ученик знает вопрос = число сочетаний 2 билетов из 19 умножить на число сочетаний 1 билета по 12 и все это поделить на число сочетаний 3 билетов по 31
4. Посчитаем второго слагаемое. Вероятность вытянуть три билета, на которые ученик знает ответ: число сочетаний 3 билетов из 19 поделить на число сочетаний 3 билетов по 31.
5. Дальше складываем то, что получили в 3 и 4.
Пиздец прогрев гоев, можно же после 9го уйти в колледж и потом в вуз поступить по внутреннему экзамену на похуй. Или вообще за границу там на еге всем похуй.
Ебать, насколько же зумеры тупые, судя по разнообразию "ответов".
от тебя говной воняет. спокнись, пидорас бля
Мгновенный разрыв птушника
Пишу правильное решение с простым рассуждением.
Долбоёб взял 3 билета. Под успешную сдачу подходят такие случаи:
знает первый и второй билет, третий не знает: 19/31 19/31 12/31
знает первый и третий, второй не знает: 19/31 12/31 19/31
знает второй и третий билет, первый не знает: 12/31 19/31 19/31
знает все три: 19/31 19/31 19/31
Итоговая вероятность это сумма вероятностей всех перечисленных случаев. Примерно 67%
О, ещё один, который не знает как разметка работает.
Скорее ещё один с плохой памятью.
Я учился в школе и ВУЗе давно, а теорию вероятностей вообще не преподавали вроде, но вот мое решение:
(19/31)*(2/3)
(19/31)*(2/3)
вот тебе полный разбор всех возможных вариантов.
для проверки даже в конце сложил вероятности проёба и удачи и да как и надо получилась единица.
Даже для неправильного решения твое решение с ошибкой. У тебя же уменьшается количество задач, которые тебе могут выпасть
Да, точно. Но вообще, решать такие задачки это дело тренировки, когда не приходится с ними сталкиваться, все забывается.
Эта задача на подумать, а не на помнить. Ты просто написал не подумав.
В 2017 сдал профильную математику на 94 балла. К репетиторам не ходил, сидел в доту играл, просто два года к ряду по-немногу задрачивал темы по матеше, но у меня маман кандидат мат. наук и препод, подсказала мне, как готовиться к этому говноэкзамену. Короче, первая же сиська по матану, теорверу, функану, алгему и прочим радостями прикладной математики была в разы сложнее любого экзамена для школьников с двузначным айсикью
мимо аспирант-математик
мимо аспирант-математик
И как же готовиться?
Берёшь задание, у него есть пул тем, которые это задание затрагивает. Разбираешься в этих темах, можешь даже скрипты решения вывести определённые, но суть скорее в понимании того, что ты делаешь, а не в решении задач по сценарию. Собственно, на этом всё. Школьники же пытаются задрочить именно варианты, надеясь, что попадётся задание, идентичное по сути своей тому, которое они чисто механически решали с репетитором. Такие дела
Этот прав.
Ну да, годно. В шкале нас училки именно задрачивали на знание алгоритма.
А потом пук среньк а чо эта вы так плохо пробник написали.
Я ума не приложу почему ни один репетитор не хочет научить школьника именно университетским методикам обучения и самообучения. Весь этот дрочь на "мы порешали сегодня полностью два варианта, поговорили об ошибках и закрепили результат"-это откровенный пиздец и высасывание денег. Вместо этого даже школьные учителя могли бы пиздюкам привить привычку разбираться в вопросе и учиться понимать, а не решать одну и ту же задачу 100 раз, как обезьянка.
сдал на 150 балов
А ты попробуй научи. Я, будучи студентом матмеха, подрабатывал репетитором. Это пиздец, я довольно быстро понял, что все мои попытки наставить школьника на путь истинный заведомо провальны. Репетиторы это понимают и просто сосут деньги, ибо вариантов нет.
Да я думаю, пиздюкам самим похуй.
Их мамка запихала к репетитору в надежде, что он не в пту пойдет, а в универ. А пиздюку похуй, у него дотка простаивает и в двач не насрано.
Я сам таким был. Сдал ЕГЭ, поступил в МухГУ и только там уже за ум взялся и начал вникать в предмет, а не просто алгоритмы задрачивать.
Школьный надроч на ЕГЭ убивает мышление, т.к. ученики привыкают искать готовый алгоритм для решения задачи. Если алгоритм не находится, то все, дальше процесс мышления не идет.
Когда читал ворчание скуфов по поводу ЕГЭ, то подкекивал и не воспринимал всерьез, но теперь понимаю, что это и правда хуита.
Никогда не было способностей к математике, начал отставать в ней от сверстников еще в 4 классе.
зато в гомосексуализме ты преуспел
Ну так "на подумать" можно и все теоремы заново вывести. Но при решении задач такого обычно не происходит, а в большинстве случаев используются готовые алгоритмы и применяются заученные математические формулы. Хотя, теория вероятностей в таких задачах не кажется слишком сложной, но ее основные законы тоже нужно помнить.
Нет, я не гей!
Ну, в целом да, я плюс минус в верном направлении думал, но сдался и загуглил
Надо посчитать количество благоприятных исходов.
Благоприятный исход 1, когда в билете все вопросы, которые ты знаешь. То есть, это количество комбинаций по 3 вопроса из 19 нам известных.
Благоприятный исход 2, когда в билете минимум 2 вопроса нам известны. То есть, это количество комбинаций по 2 вопроса из 19 нам известных умножить на количество комбинаций из 1 из 12 нам неизвестных, то есть просто 12 вопросов.
Ну, а чтобы посчитать найти вероятность, нам надо сумму благоприятных исходов поделить на все исходы, то есть количество комбинаций из 31 по 3.
Надо посчитать количество благоприятных исходов.
Благоприятный исход 1, когда в билете все вопросы, которые ты знаешь. То есть, это количество комбинаций по 3 вопроса из 19 нам известных.
Благоприятный исход 2, когда в билете минимум 2 вопроса нам известны. То есть, это количество комбинаций по 2 вопроса из 19 нам известных умножить на количество комбинаций из 1 из 12 нам неизвестных, то есть просто 12 вопросов.
Ну, а чтобы посчитать найти вероятность, нам надо сумму благоприятных исходов поделить на все исходы, то есть количество комбинаций из 31 по 3.
Тогда почему у тебя аниме к постам прилеплено?
/тред
Возможно, ты имеешь в виду другие алгоритмы, типа решение по образцу, но алгоритмы в любом случае приходится применять. Например, ты не выводишь каждый раз заново теорему Пифагора, а заучиваешь готовую формулу. Потом, в задаче применяешь эту и другие формулы и получаешь ответ. Да, нужно понимать, где и как применить эти формулы и законы, но их заранее уже нужно знать, буквально заучить, как таблицу умножения. То есть формулы и законы это и есть алгоритмы в моем понимании, без которых, какой бы ты ни был гений, ты мало что сможешь. Это буквально математический язык, слова, которые ты сначала запоминаешь, а потом учишься складывать в предложения.
>комбинаций
Говори правильно: сочетаний
В ру-литературе по дискретной математике точно пишут сочетания, но я просто с детства тупой и для меня легко запомнить типо C это обрезок от combine - комбинация
Русский язык вообще всратый какой-то.
Сочетания, перестановки, размещения. Каво блять?
Хотя будто где-то проебался, почему я решил подставить крайние значения, а-ля, знаю 30 вопросов из 31 и вероятность сдачи экзамена равна 1 тупа, аноны-математики где я насрал в штаны?
Какие крайние значения? Такого в задаче нет.
Все верно ты расписал, это задачка для дебилов.
Вместо того, чтобы дробь посчитать, надо на два шага больше сделать и подсчитать комбинации.
Это даже не со звездочкой задачка.
Ай, сорри, я тупой, просто если нам выпадет билет с тем самым вопросом, который мы не знаем, а в случае если мы выучили 30 вопросов из 31 он будет буквально только один, мы всё равно сдадим экзамен, поэтому вероятность и равна 1.
Хотя это забавно чутка, ибо вероятность успеха, что в случае если выучим все вопросы, что в случае если не выучим только один, одинаковая
Где-то 84 процента.
3 × (19 × 18 × 12) / (31 × 30 × 29) = 45,6%
Долго думал, надеюсь правильно. Примерно 0.672
А если бы этот пидорас выучил все вопросы, то и проблемы бы не было.
Ибо по условию задачи нам надо минимум на 2 ответить только
Хотя ИРЛ препод всё равно душить начнёт, помню на пересдаче по дискретной матеше мне препод задал вопрос, как из сочетаний можно получить размещения, и тупа посыпался, но благо я на 3 уже ответил и мне он подсказал внимательно посмотреть на их формулы и я тогда догадался.
А вот и попался дурачок с двузначным IQ, для абсолютного успеха надо только 30 вопросов выучить.
Как было написано выше, для успешной сдачи нужно учить ответы, а не вопросы.
А можно ли знать ответ не зная вопроса? ДУМАЕМ...
Ты прав. Но тогда интересно пойти дальше и посчитать сколько нужно выучить вопросов, чтобы вероятность успеха была приемлемой. Например 95 или 99 процентов.
Да это тащем-то легко, просто пишем функцию на любом ЯП, я даже ради хохмы на питоне наструячу
Знание вопроса не означает автоматического знания ответа на вопрос.
from math import comb as C
all_c = C(31, 3)
def P_A(k):
good1 = C(k, 3)
good2 = C(k, 2) * C(31 - k, 1)
return ( good1 + good2 ) / all_c
for i in range(31, 1, -1):
print("Количество выученных билетов - %d" %i, P_A(i))
Как-то так
Да я пошутил, это то очевидно
>om math import comb as C
Пхютхонодебил высрался
Блять, могу и на плюсах наструячить
А, вот хуй, ты меня троллишь, но я бы мог показать тебе красивую функцию, которая считает факториал очень быстро и эффективно, но ты не оценишь...
Я оценю
Через динамическое программирование небось?
Да она супер очевидная, жаль, что факториал самая быстрорастущая функция и мы быстро попадаем в overflow, после 20 уже хуйня пошла
Так точно
#include <iostream>
unsigned long long f[32];
void factorial(unsigned long long previous, unsigned long long next)
{
next *= previous;
}
int main()
{
f[0] = 1, f[1] = 1;
for (unsigned i = 2; i < 32; i++){
f = i;
factorial(f[i - 1], f + i);
}
for (unsigned i = 0; i < 32; i++)
std::cout << i << " " << f << std::endl;
return 0;
}
Блять, София, почему ты меня не поцеловала и я должен страдать от любви к той, что я не могу даже понять
Бля чувак, ну ты прям америку открыл
Пиши на чистом Си.
Читай пост внимательнее, ё-пта
Та ничего не изменится, кроме вывода данных в консоль
в 2014 сдавал, когда ещё разделения не было. Основная часть и несколько заданий из С - легкотня. Хотя, я ни одной теоремы, кроме Пифагора не знал (геометрия в 1 части тупо логикой решалась). 71 балл набрал, вроде. А преподы говорили, что я троечник-даун. Дал и пососать, когда любимчиков обогнал. сука ёбаная классуха
Вероятность того, что ученик сдаст контрольную, составляет примерно
66.65%
>Вероятность того, что ученик сдаст контрольную
Ребёнок, при чём тут динамическое программирование и зачем ты переусложнил то, что вычисляется в один цикл?
Максимум в чём усложнил, то это вызов функции factorial, хотя пи факту это одна строчка кода, а в остальном ты не прав, это как раз динамическое программирование, как и при вычислении чисел Фибоначчи
Патаму что приставь что мы считаем факториал не 19 а не 1000000.
Про вред преждевременной эякуляции оптимизации ему еще не рассказали, это только на втором курсе будет.
Тут единственная адекватная оптимизация в том, что мы сохраняем значение факториала в массив/память, только так вычислять факториал и нужно, иначе на слишком больших числах стэк вызовов ебанётся нахуй из-за рекурсии
1000000, для GMP-числа нужно будет байтов 800, наверное, это у нас 800 * 10^6 байт, итого 800Мбайт, ну да, в куче столько памяти нет ...
3 × (19 × 18 × 12) / (31 × 30 × 29) + (19 × 18 × 17) / (31 × 30 × 29) = 67,2%
Первое слагаемое учитывает случаи, когда ответит на 2 вопроса из 3 , а второе слагаемое учитывает когда ответит на все вопросы.
В сильных классах с сильными детьми именно учат думать и доказывать всё. В остальных случаях это заведомый проеб усилий и времени.
Ты прав, анон. Я не сделал поправку на приличные школы с гуманитарным уклоном, ну и школы для, так сказать, пролетариата, где детям вряд ли вообще хоть какие-то знания понадобятся в жизни
Для 95% достаточно 27 вопросов знать, для 99% достаточно 29 вопросов.
Спасибо, что мне не надо писать ответ.
Впервые за год зашел на двач, двачеры все такие же тупые.
Пожалуйста, а в чем именно их тупость?
Откуда картинка?
Первый правильный ответ только спустя 80 постов (я не смог долистать).
41 пост
Дегенератиксы)))))
19/31 и будет))))
ебать 279 постом
19/31 и будет))))
ебать 279 постом
>Патаму что приставь что мы считаем факториал не 19 а не 1000000
Да хоть миллиарда, этот "алгоритм" ничем не помогает.
Ты ведь ни слова не понимаешь из того, что написал.
Для решения этой задачи сначала определим, сколько вопросов ученик знает и сколько вопросов ему нужно правильно ответить для успешной сдачи контрольной.
Ученик знает 19 вопросов из 31. Для сдачи контрольной ему нужно ответить правильно на 2 из 3 предложенных вопросов.
Теперь рассмотрим возможные варианты:
1. Ученик знает 2 вопроса из 3.
2. Ученик знает 1 вопрос из 3.
3. Ученик не знает ни одного вопроса из 3.
Теперь посчитаем вероятность каждого из этих случаев.
Обозначим:
- \( K = 19 \) — количество известных вопросов.
- \( N = 31 \) — общее количество вопросов.
- \( M = 3 \) — количество предложенных вопросов.
### 1. Вероятность, что ученик знает 2 вопроса из 3
Количество способов выбрать 2 известных вопроса из 19:
\[
C(19, 2) = \frac{19!}{2!(19-2)!} = \frac{19 \times 18}{2} = 171
\]
Количество способов выбрать 1 неизвестный вопрос из 12 (31 - 19):
\[
C(12, 1) = 12
\]
Общее количество способов выбрать 3 вопроса:
\[
C(31, 3) = \frac{31!}{3!(31-3)!} = \frac{31 \times 30 \times 29}{3 \times 2 \times 1} = 4495
\]
Общее количество благоприятных исходов для этого случая:
\[
171 \times 12 = 2052
\]
### 2. Вероятность, что ученик знает 1 вопрос из 3
Количество способов выбрать 1 известный вопрос из 19:
\[
C(19, 1) = 19
\]
Количество способов выбрать 2 неизвестных вопроса из 12:
\[
C(12, 2) = \frac{12!}{2!(12-2)!} = \frac{12 \times 11}{2} = 66
\]
Общее количество благоприятных исходов для этого случая:
\[
19 \times 66 = 1254
\]
### 3. Вероятность, что ученик не знает ни одного вопроса из 3
Количество способов выбрать 3 неизвестных вопроса из 12:
\[
C(12, 3) = \frac{12!}{3!(12-3)!} = \frac{12 \times 11 \times 10}{3 \times 2 \times 1} = 220
\]
### Общее количество благоприятных исходов
Теперь сложим все благоприятные исходы:
\[
2052 + 1254 + 220 = 3526
\]
### Вероятность успешной сдачи контрольной
Теперь мы можем найти вероятность того, что ученик сдаст контрольную:
\[
P = \frac{3526}{4495}
\]
Таким образом, вероятность того, что ученик сдаст контрольную, составляет:
\[
P \approx 0.785
\]
Или, в процентах, примерно 78.5%.
Ученик знает 19 вопросов из 31. Для сдачи контрольной ему нужно ответить правильно на 2 из 3 предложенных вопросов.
Теперь рассмотрим возможные варианты:
1. Ученик знает 2 вопроса из 3.
2. Ученик знает 1 вопрос из 3.
3. Ученик не знает ни одного вопроса из 3.
Теперь посчитаем вероятность каждого из этих случаев.
Обозначим:
- \( K = 19 \) — количество известных вопросов.
- \( N = 31 \) — общее количество вопросов.
- \( M = 3 \) — количество предложенных вопросов.
### 1. Вероятность, что ученик знает 2 вопроса из 3
Количество способов выбрать 2 известных вопроса из 19:
\[
C(19, 2) = \frac{19!}{2!(19-2)!} = \frac{19 \times 18}{2} = 171
\]
Количество способов выбрать 1 неизвестный вопрос из 12 (31 - 19):
\[
C(12, 1) = 12
\]
Общее количество способов выбрать 3 вопроса:
\[
C(31, 3) = \frac{31!}{3!(31-3)!} = \frac{31 \times 30 \times 29}{3 \times 2 \times 1} = 4495
\]
Общее количество благоприятных исходов для этого случая:
\[
171 \times 12 = 2052
\]
### 2. Вероятность, что ученик знает 1 вопрос из 3
Количество способов выбрать 1 известный вопрос из 19:
\[
C(19, 1) = 19
\]
Количество способов выбрать 2 неизвестных вопроса из 12:
\[
C(12, 2) = \frac{12!}{2!(12-2)!} = \frac{12 \times 11}{2} = 66
\]
Общее количество благоприятных исходов для этого случая:
\[
19 \times 66 = 1254
\]
### 3. Вероятность, что ученик не знает ни одного вопроса из 3
Количество способов выбрать 3 неизвестных вопроса из 12:
\[
C(12, 3) = \frac{12!}{3!(12-3)!} = \frac{12 \times 11 \times 10}{3 \times 2 \times 1} = 220
\]
### Общее количество благоприятных исходов
Теперь сложим все благоприятные исходы:
\[
2052 + 1254 + 220 = 3526
\]
### Вероятность успешной сдачи контрольной
Теперь мы можем найти вероятность того, что ученик сдаст контрольную:
\[
P = \frac{3526}{4495}
\]
Таким образом, вероятность того, что ученик сдаст контрольную, составляет:
\[
P \approx 0.785
\]
Или, в процентах, примерно 78.5%.
Гопоте бесполезно давать задачи сложнее уровня третьего класса.
>не переусложнил
Ну сравни, ёпта
Ты слишком оптимистичен
Ну, если цель получить только факториал числа n, то задача выполнена просто прекрасно, но вот в процессе вычисления комбинаций нужно несколько раз обращаться к факториалам, если не сокращать.
0,4691879
> в процессе вычисления комбинаций нужно несколько раз обращаться к факториалам
Кто же в здравом уме вычисляет факториалы при вычислении сочетаний?
Имел в виду, чтобы считать мощность сочетаний, хуйню сказал, да, абсолютно некорректно,
Блять, а я думал он просто так их считает.
Конечно. Там абонимент





























"Ученик знает 19 вопросов из 31. Для сдачи контрольной достаточно ответить на два вопроса из предложенных трёх. Какова вероятность того, что ученик сдаст контрольную?"