Весёлый бамп.
Вверх! Ввысь!
Да кто тут бампает, если это не ОП?
Вся нулевая в дерьме. Один сыч собрался на драку, второй сидит в фап-тредах с трапами, третий хочет тяночку.
Аноны, давайте разбавим этот приевшийся негатив интересной математикой.
Аноны, давайте разбавим этот приевшийся негатив интересной математикой.
в биопроблемном мире нет места математике
Ну если бы только сумма диагональных элементов была равна нулю, и они были бы эрмитовыми, то всё было бы очень просто, а так хз.
Рассмотри несколько таких определителей, составь базис по матрицам, заметь закономерность и по индукции докажи, хули ты.
А, только 2х2. Тогда хз, надо думать
Т. к. ограничение всего одно, то базис будет состоять из трёх векторов. Что-то типа (1, 0, -1, 0) (1, -1, 0, 0) (0, 1, 0, -1).
А вот более конкретно подобрать у меня не получается что-то.
Хватит троллить.
Каким образом в 4-мерном пространстве может быть меньше 4 базисных векторов?
есть догадка, что
(1, 0)
(0, -1)
и она же, но транспонированная
(1, 0)
(0, -1)
и она же, но транспонированная
Оно двухмерное. Матрицы 2х2.
Элементарными преобразованиями мы можем привести матрицу к нулевой строке/столбцу, при этом свойство сохранится. Получается у нас будет 1 базисный вектор в системе, зависящий чисто от свободной неизвестной
Возможно, надо проверить.
Но ведь чтобы определить вообще любую матрицу 2х2 базисными, нужны 4 матрицы.
1, 0
0, -1
Да. Но заметь фишку: здесь мы вводим одно ограничение на пространство. Это уже не просто четырёхмерное пространство. Это четырёхмерное пространство, где все элементы матриц в сумме дают ноль.
Факт в том, что из-за этого ограничения базис будет состоять из трёх матриц.
Скорее всего, (1, -1, 0, 0), (0,0, -1, 1) и ... нужно что-то подобрать. Сейчас попробую.
Пространство это трехмерно - гиперплоскость x11+x12+x21+x22 = c. Базисом служит любой набор линейно независимых матриц из данного пространства. Например (c, 0, 0, 0), (0, с, 0, 0) , (0, 0, с, 0).
Да? Тогда попробуй через этот базис вычислить (-1, 0, 0, 1). То-то же.
Че, линейная алгебра уже на первом курсе тяжело тебе даётся?
Нет, так же, как и всё остальное.
>Пространство это трехмерно - гиперплоскость x11+x12+x21+x22 = c. Базисом служит любой набор линейно независимых матриц из данного пространства.
Верно.
>Например (c, 0, 0, 0), (0, с, 0, 0) , (0, 0, с, 0).
Неверно, твои базисные матрицы самому пространству не принадлежат.
Очевидно же. Зачем ты к матрицам прикопался, будем с 4-х мерными векторами работать. Первые три переменные мы можем выбирать произвольно, а четвертая зависит от суммы первых трех — пространство таких векторов трехмерно. Базисом будет:
(1, 0, 0, -1), (0, 1, 0, -1), (0, 0, 1, -1)
С помощью этих векторов мы можем выбрать желаемые значения для первой, второй и третей позиции вектора, а четвертая «подстроится» под их сумму.
(1, 0, 0, -1), (0, 1, 0, -1), (0, 0, 1, -1)
С помощью этих векторов мы можем выбрать желаемые значения для первой, второй и третей позиции вектора, а четвертая «подстроится» под их сумму.
Похоже на правду.
(1,1,-1,-1);(1,-1,1,-1);(1,-1,-1,1)
или можно так:
(1,-1,0,0);(1,0,-1,0);(1,0,0,-1)
/thread
Спасибо, разобрался.
Сейчас попробую другие темы порешать.
Сейчас попробую другие темы порешать.
С точностью до нумерации координат, (-1-,0,0,1) = -1(1,0,0,0) + 0 (0,1,0,0)+ 1*(0,0,0,1)
Принадлежат же, подставь в уравнение.
Упс, наврал, они принадлежат, просто они не являются линейно независимыми. Правильный базис дал анон тут:
Итак, анон, второй рубеж.
Всё просто, как вырезка тыкв на недавний Хэллоуин.
У нас есть единичная матрица 2х2 и мы пытаемся посчитать её собственной значение, чтобы составить базис из собственных векторов.
Внимание, вопрос: почему же собственный базис получается вида 2х1, а не 2х2? В чём ошибка?
Всё просто, как вырезка тыкв на недавний Хэллоуин.
У нас есть единичная матрица 2х2 и мы пытаемся посчитать её собственной значение, чтобы составить базис из собственных векторов.
Внимание, вопрос: почему же собственный базис получается вида 2х1, а не 2х2? В чём ошибка?
Пространство матриц размером NxN имеет размерность N^2, но вот собственные вектора матрицы - это базис в линейном пространстве N (в том пространстве, где матрица является линейным оператором), а не в линейном пространстве самих матриц.
То есть, в матрице (1, 1, 1, 1), например, будет всего один собственный вектор?
Живительный бамп во имя света.
Алсо, я тут недавно закончил школу и целенаправленно поступил в шарагу регионального уровня, чтобы оставить себе как можно времени на хобби и двачевание. Т. к. это шарага, для более-менее внятного изучения приходится искать материалы в интернете.
Так вот, анон: почему в тырнетах так много инфы для школьников-физматовцев, а для студентов вообще ничего нет? Это же несправедливо. Ты можешь вбить в гугл любую школьную тему по математике и в ответ получишь целую тысячу различных статей и видео.
Зато шансы на успех понижаются в десятки раз, если ты решишь загуглить что-то из студенческой программы.
Это что, студенты не люди? Отчего всё так не кошерно?
Так вот, анон: почему в тырнетах так много инфы для школьников-физматовцев, а для студентов вообще ничего нет? Это же несправедливо. Ты можешь вбить в гугл любую школьную тему по математике и в ответ получишь целую тысячу различных статей и видео.
Зато шансы на успех понижаются в десятки раз, если ты решишь загуглить что-то из студенческой программы.
Это что, студенты не люди? Отчего всё так не кошерно?
Бамп во имя нерешённой задачи.
Для начала нужно посмотреть, будет ли это пространством. А потом уже базис искать.
У ней два собственных значения и два собственных вектора -
www.mathportal.org/calculators/matrices-calculators/matrix-calculator.php?formId=1&val1=1%3A1%3Anull%3Anull%3Anull%3Anull%3B1%3A1%3Anull%3Anull%3Anull%3Anull%3Bnull%3Anull%3Anull%3Anull%3Anull%3Anull%3Bnull%3Anull%3Anull%3Anull%3Anull%3Anull%3Bnull%3Anull%3Anull%3Anull%3Anull%3Anull%3Bnull%3Anull%3Anull%3Anull%3Anull%3Anull&val2=2&val3=2&rb1=evec
Не пойму, как нашли второе собств. значение?
И да, справедливости ради, утверждение "собственные вектора матрицы - это базис в линейном пространстве N" это верно разве что для эрмитовых матриц.
нашли корни характеристического многочлена
www.mathportal.org/calculators/matrices-calculators/matrix-calculator.php?formId=1&val1=1%3A1%3Anull%3Anull%3Anull%3Anull%3B1%3A1%3Anull%3Anull%3Anull%3Anull%3Bnull%3Anull%3Anull%3Anull%3Anull%3Anull%3Bnull%3Anull%3Anull%3Anull%3Anull%3Anull%3Bnull%3Anull%3Anull%3Anull%3Anull%3Anull%3Bnull%3Anull%3Anull%3Anull%3Anull%3Anull&val2=2&val3=2&rb1=char
Читай английскую вики, там матана студенту более чем достаточно.
Опчик, какой курс? Первый небось
Ай-яй-яй. Я дурак, просто стандартная ошибка в расчётах. Спасибо, продолжаю полёт.
Сейчас почитаю тщательно в гугле про алгоритм Грама-Шмидта и снова продолжу пытаться что-то решать.
Да.
Сука пиздец. Блядь пидорас, есть ебаное пространство векторов двумерное, ебаный твой рот. На нём, блядь, действуют сраные линейные преобразования, которые, блядь, представляются матрицами (сука блядь надо умножить матричку на вектор). У этого ебаного оператора есть собственные векторы в ебаном пространстве. Не матрицы, блядь, а вектора блядь. На них оператор действует, блядь, только растяжением (умножил матричку на сраный вектор, получил его же, но с коэффициентом). Для большинства матриц, блядь, можно найти столько таких ебаных векторов, какова размерность сраного пространства.
Вот тебе примеров на клык:
((1, 0), (0, 1))v = v для любого v = (v1, v2). Значит юлядь любой вектор блядь собственный! О как охуенно! Потому, что единичная матрица нихуя с твоими векторами не делает! Выбирай, сука, хоть (1, 0), (0, 1),
хоть (1488, 666), (228, 0).
((1, 1),(1, 1))(1, 1) = (2, 2) = 2(1, 1), значит, блядь,
(1, 1) - собственный, блядь, вектор! Ну блядь ещё хуйнём.
((1, 1),(1, 1))(1, -1) = (0, 0) = 0(1, 1). Опана нахуй! Тоже собственный! Вот тебе, блядь, и базис собственный (векторного пространства, не матриц, блядь) (1, 1), (1, -1).
Один собственный вектор в анусе будет.
((a, 1), (0, a)) и вот у такой матрицы.
А в исходной задаче любых три независимых матрицы с таким свойством! Хоть, блядь ((1488, 666),(-2154, 0)),
((228, -228),(0, 0)), ((0, 1),(0, -1)). Три, сука, потому, что одно уравнение в 4-пространстве. А вообще-то блядь - вообще по хуям, что это матрицы, условие естественное для векторов, можно смотреть как на 4-векторы, блядь.
Ебать тут блядь пиздец на хуй. Пиздец, блядь, ох я ебал. Охуеть, блядь!
Спасибо за доходчивое пояснение.
тёлка была?
Не выебывайся.
вот у этого тёлки были я про него читал
а у тебя тёлка была?
ну типа 4 элемента матрицы значит 4 мерное пространство, но сумма равна 0, значит 1 из эдементов выражается через другие, то есть 3 "степени свободы" у твоей матрицы, то есть берешь ЛЮБЫЕ 3 линейно независимые матрицы, сумма элементов которых 0. Это и будет базис
аааааааааааааа
АААААААААААААА\
В первой задаче линейное пространство будет только если сумма равна нулю. Если же просто равна константе C != 0 то нихуя не линейно, потому и наобум взятые линейно независимые три вектора базис нихуя не образовывают так как их линейная комбинация не замкнута относительно пространства.
Всё, алгоритм довольно простой.
Сейчас потренируюсь ещё и всё у меня будет хорошо.
Вопросов больше не осталось.
Двачик, ты герой. С тобой разобраться было намного проще.










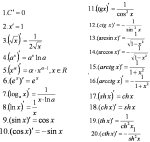









Так вот. Как будет выглядеть базис в таком пространстве?
Ты не моя личная армия, но помощь нужна очень. По ходу разбора тем буду бампать подобными вопросами.