бамп
Сеня
От нас что требуется
вот вам для размышления
рєбят алло матіматіка?) да да для любого єпсілон больше нуля с какими словами вы мне хуй сосали напомните)))
Математика не нужна. Я создал сверхэффективный ИИ, архитектуру, превосходящую все остальные, не зная ничего из математики. В свою очередь математики сосут хуйца уже которое десятилетие
>Сумбурно написано это всё, я знаю.
Ты упоролся что-ли? Въеби арифметику Пеано для начала и не еби мозги анонам.
> f(x)=x+1
Вообще даже не близко в этом контексте. Функциональная зависимость не обязательно есть последовательность операций. Ну, то есть конечно можно определить функцию таким образом, и так обычно и делают, но вообще можно просто задать два множества, и биективно отобразить одно в другое стрелочками, порядковыми номерами, да как угодно, не прибегая к арифметике и алгебре.
Разложение простого функционального преобразования в композиционное может и полезно в процессе анализа, но в данном случае это просто словоблудие.
тут про другое и не про пеано
>но в данном случае это просто словоблудие
Вот именно, это сложно даже сейчас понимать из-за этого. Я не про тебя, я про себя.
Вот лучше посмотри на пики. Выходит что объект справа можно определить как ровно тот же объект но с неким дополнением в левой части?
Это про пик 1.
А вот пик 2 это ещё более смутно. Давай знаешь я перепишу пик 2 на пик 3.
Представь есть какой-то символ В. Можно декларировать, что символ В подразумевает другие символы или, в нашем случае, символ В'.
Когда я пишу что он "подразумевает" - я имею ввиду тот самый большой кружок, что должен, ассоциациями говоря, "собирать" В из В'.
Но тогда выходит что символ В это не только символ, но ещё и определение некого "собирания" из символа В'.
И если уж мы тут начнём тогда говорить за определения, то выходит словно вещь в своём определении имеет саму же себя(стол это стол), но по существу это не так, потому что в одном случае справа это символ, а в другом случае это некий может... процесс? Хм.
От буквы к слову
Что буква
От буквы к слову
Что буква
.
.
.
Хм. Ничо непонятно
Что буква
От буквы к слову
Что буква
.
.
.
Хм. Ничо непонятно
да подбяпшивает его немного как меня щас на депривации ебаный в рот ребят как говорится мдаа баляя ебать ево в рот)))
>подбяпшивает
чо ето значит
3/4.
ну подтрунивает хз как сказать))
ай вос триппинг олл найт вайл ай воз слиппинг
ребзь что значит когда говорят я играю лоббі даже когда сплю 💀💀💀
Test
💀💀💀
хуйца моево тестирует гагага))
Сеняяя привет сладенький кисик ты мой чмок
0_0
а ти кто
Твой старый друк (не)математик в дисике
Я думаю я помню тебя.
Ты мне предлагал в ну поступить же.
Ну можно туда походить ради интереса
Не еби мозги с вечера
Ради аниме походить жеж. Ну сил нет щас.
А всё проще оказалось. Жесц


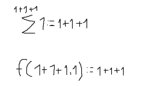







А тогда как запись основанная на символах подразумевает каждый символ записи выполняется, то 4 это не просто символ, это сокращение символа 1+1+1+1 что подразумевает f(f(f(1))).
Тогда можно задачи про n=m воспринимать как задачу о восстановлении изначальной записи N, да такой записи для которой можно было бы сказать, что N это буквально тоже самое что и M, только вот где M в свою очередь это не просто запись, а некая динамическая запись.
Когда я написал f(f(f(1))) я вам дал понять что здесь происходит порядок выполнения неких действий. Ну, не обязательно порядок - но действия происходить должны.
Сумбурно написано это всё, я знаю. Может позже более норально оформлю, а так довольствуетесь raw imput