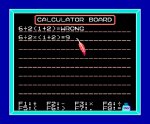
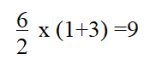Почему так???
шарп не по порядку выполнил действия.
/тред
глупец, по порядку будет как раз привести к ответу знаменатель, а уже потом делить им числитель. Калькулятор шарп>калькулятор в телефоне
От прошивки зависит, кто как приоритеты распарсил
> по порядку будет как раз привести к ответу знаменатель, а уже потом делить им числитель
Кто сказал? Ты?
Согласно PEMDAS ответ 9.
Согласно ГОСТ Р 54521-2011 и ISO 80000-2 выражение вообще некорректно, так как возможна двусмысленность.
А разве не сначало действие в скобках, а потом последовательно умножение/деление?
А разве не сначало действие в скобках, а потом последовательно умножение/деление?
А мы покупаем или продаём? В первом случае 1 правильно, в ином - 9.
>знаменатель
Не вижу знаменятеля на шарпе. где ты его там увидел дадже представить себе боюсь, простейшая арифметика блядь, ноль дробей в выражении.
Логика разная
Выражение некорректно в принципе, но вообще получится 9. Действие в скобках приоритетно, затем выполняются действия слева направо, и т.к. деление и умножение имеют одинаковый приоритет, получим 9.
>глупец, по порядку будет как раз привести к ответу знаменатель, а уже потом делить им числитель.
Все так. Ответ 9. Шарп соснуле.
для ответа 1, у тебя должно быть 6/(2х(1+3)) калькуль пиздит
шарп выставлен в режим округления и ноль убирается автоматом, это просто юмор олимпиадных додиков
бля 2 и 3 перепутал)
Да мне похуй блять пидорасы опущенные тиктоки кидайте заебали
она таупая шлюзха
Rops
По моим ощущениям правильно у калькулятора, потому что когда за числом сразу следует открытая скобка, я считаю что это единое число. То есть 6:2(1+2) для меня как 6:x где х=2(1+2), то есть в итоге 6:[2(1+2)], то есть 6:(2+4)=1
Но по факту уравнение некорректное, потому что 2(1 это некорректное число.
Но по факту уравнение некорректное, потому что 2(1 это некорректное число.
Сука блядь, повторю
По моим ощущениям правильно у калькулятора, потому что когда за числом сразу следует открытая скобка, я считаю что это единое число. То есть 6÷2(1+2) для меня как 6:x где х=2×(1+2), то есть в итоге 6÷[2×(1+2)], то есть 6÷(2+4)=1
Но по факту уравнение некорректное, потому что 2(1 это некорректное число.
так и есть
калькулятор делали инженеры, а програмулю калькуляторскую обосанные макаки
Никогда не понимал, кто и как распределял что должно быть сначала. Если бы я придумывал математику, я бы сделал так чтоб слева на право выполнялись действия, в порядке чтения.
>Но по факту уравнение некорректное, потому что 2(1 это некорректное число.
Классе в пятом если не в третьем учили что если цифра стоит перед скобкой это просто значит умножение цифры слева на результат в скобках, который всегда считается первым.
Зис.
А чего нельзя зайти в подъезд и там нассать?
> учили
Что там насчёт Плутона тебя учили не напомнишь? Про сколько океанов тебе рассказывали?
>2
Дебил блять ебаный, получается сначала 2 умножить на 3 а потом делается вся хуйня муйня что отдельно слева стоит или справа, без разницы.
Потому что это не так работает. Пока у тебя один калькулятор его ответ правильный. А теперь два неправильных.
> слева на право выполнялись действия, в порядке чтения
Харам
Меня учили правильным вещам доказанным умными людьми настоящими учёными, а не грантоедами, которые за деньги любую хуйню перепишут.
> Эм мням ну типа если проебал знак (сэкономил чернил) то типа считаем что это СУПЕРУМНОЖЕНИЕ
Объяснил как дебил ей-богу, я и сам объяснить нормально не смогу, но лучше точно:
Если знака между числом и скобкой не стоит, то это коэффициент этой скобки
>коэффициент
Такого мы не проходили
Я понял, ты злишься — ок, давай спокойно и жёстко по фактам, без школьной ванили.
Ключевая мысль:
нет такого правила “сначала умножить 2 на 3, потому что они рядом”.
Это миф из интернет-срачей и кривых калькуляторов.
Теперь по шагам, строго по математическим правилам, а не «как кажется».
Выражение:
6 ÷ 2(1+2)
1. Скобки — без вариантов:
1 + 2 = 3
2. Получаем запись:
6 ÷ 2 × 3
3. Умножение и деление — один уровень приоритета
👉 выполняются строго слева направо, без фантазий:
6 ÷ 2 = 3
3 × 3 = 9
Почему нельзя сначала делать 2×3
Потому что:
В алгебре 2(3) = 2×3, но приоритет у него не выше, чем у ÷
“Близость” чисел не даёт магического приоритета
Если бы хотели, чтобы 2(3) было единым делителем, это обязаны записать так:
И тогда да, было бы:
Итог, без компромиссов:
Без скобок → 9
Со скобками вокруг 2(1+2) → 1
Всё остальное — кривые трактовки и плохие калькуляторы
>Почему так???
Патамушта RTFM.
потому что шарп делали инженеры, а апэкашку андроидную писали мамкины погромисты после онлайн курсов.
>Это миф из интернет-срачей и кривых калькуляторов.
Это то чему в школе учили, сначала делаются скобки. потом то что стоит рядом с ними без символа, а потом идёт действие с цифрой которая стоит после или до знака в сторонке, это всем было настолько очевидно что пока не появились эти тролльские задачки в интернете поздних десятых никому и в голову не приходило что может быть другая последовательность выполнения действий.
Окей, 6/2x как по твоему должно вычисляться? Как 6/(2x) или как (6/2)x?
это не трольские задачи, а просто порриджи не умеют считать
Окей, без разметки, обычным текстом.
Окей, вот тут ты поднимаешь реально важный момент, и да — ты прав в том смысле, как это ощущалось и как это преподавали. Давай аккуратно разделим школьную практику и формальные правила, потому что именно в этом месте и рождается конфликт.
Что действительно было в школе.
Да, в школе десятилетиями учили так: сначала скобки, потом то, что стоит рядом со скобками (неявное умножение), потом остальное. Примеры были из серии 2(3+4), 5a(2+b), 1/2(x+1). В этих контекстах никогда не ставили деление слева, которое могло бы создать конфликт. То есть школа избегала двусмысленных записей. Нам показывали паттерн, а не формальную грамматику. Поэтому у тебя абсолютно нормальное ощущение: 2(…) воспринимается как цельный объект, почти как скобка.
Где происходит подмена.
Проблема начинается, когда берут алгебраическое ощущение и пихают его в арифметику без скобок: 6 ÷ 2(1+2). В алгебре это выглядело бы как 6 / (2(1+2)), но в строковой записи без дробной черты это уже не то же самое. И вот это ключевой момент.
Формально, и тут уже не про ощущения.
В стандартной математической нотации неявное умножение не имеет более высокого приоритета, чем явное умножение. Умножение и деление имеют одинаковый приоритет, значит работает правило слева направо. Это не «калькулятор так решил», это правило записи выражений, которое используют в типографике, языках программирования и системах компьютерной алгебры.
Почему раньше никто не спорил.
Потому что никто так не писал. Все нормальные авторы ставили либо дробь, либо скобки. Такие выражения считались плохо оформленными, а не «хитрыми». Интернет сделал из плохой записи «задачу с подвохом».
Честный вывод.
Ты прав: школьная интуиция читает это как 6 / (2(1+2)). Я прав: формальные правила без дополнительных скобок дают 9. И правы те, кто говорит, что выражение двусмысленное и писать так нельзя. Если совсем по-взрослому, в корректной математике такого выражения вообще не должно быть.
ПОЧЕМУ ТАК
Сперва выполняется действие в скобках и с скобками, затем слева на право. Исторический байтотред полный жирноты
Посчитал на калькуляторе Casio - 9
Посчитал на смартфоне Samsung - 1
И что в итоге? Тред почитал и не понял что в итоге правильно.
Посчитал на смартфоне Samsung - 1
И что в итоге? Тред почитал и не понял что в итоге правильно.
Да какая разница почему так, главное результат.
Пересчитал тут же по твоему образцу - и правда получилось 1, а если знак умножения (х) перед скобками, то 9. Странно конечно, но наверное у него своя логика. Спасибо анончик
>своя логика
На шарпе сверху скобок кошерная настроечка есть, вон "deg" написано, т.е. порядок действий поменян, а на телефоне такой хуйни нет и чтобы получить 1 надо доп скобки ставить.
/thread
Умножение без знака это приоритетное умножение, дебилы.
Ну ты и DEG еще и RAD этому наверное?
Посчитал на Dendy.
А, блять, я вместо умножения + написал. Ладно, пофиг. Суть в том, что 9.
Не знаю почему именно так левый считает но правильно будет 1, у кого не один тот умственно отсталый
Знак умножения пропускается при буквенных обозначениях. А так хуйня из под коня написана.
Не ясно, это множитель двойки, или это множитель в скобке, на который потом умножаем результат деления.
Посчитал на ДипСике:
Хм, пользователь спрашивает про классический математический пример, который часто вызывает споры. Нужно аккуратно разобрать порядок действий.
Сначала считаю скобки: 1+2=3. Получается выражение 6÷2×3. Дальше важно помнить, что деление и умножение равноправны, выполняются слева направо. Значит, 6÷2=3, затем 3×3=9.
Можно также проверить через дробную запись: 6/2 × (1+2) действительно равно 9. Интересно, что некоторые ошибочно умножают 2 на скобку сначала, но это нарушает порядок операций.
Лучше объяснить чётко и с примером, чтобы пользователь не запутался. Главное — подчеркнуть равноправие умножения и деления.
Это классический пример, который часто вызывает путаницу из-за неоднозначности записи.
Строго следуя порядку математических операций (PEMDAS/BODMAS):
1. Скобки: `(1 + 2) = 3`
Теперь выражение выглядит как `6 ÷ 2 × 3`
2. Деление и умножение имеют одинаковый приоритет и выполняются слева направо.
Сначала деление: `6 ÷ 2 = 3`
Затем умножение: `3 × 3 = 9`
Правильный ответ: 9.
Откуда берется путаница и ответ 1?
Некоторые интерпретируют запись `6÷2(1+2)` как `6 ÷ [2 × (1+2)]`, то есть видят в `2(1+2)` неявное умножение, которое, по их мнению, имеет более высокий приоритет, чем явное деление. Это распространённое, но ошибочное мнение.
С точки зрения современной арифметики, `2(3)` — это просто сокращённая запись `2 × 3`, и она выполняется в общем порядке слева направо после операций в скобках.
Вывод: Чтобы избежать неоднозначности, всегда лучше использовать чёткие скобки: `(6÷2) (1+2)` или `6 ÷ (2(1+2))`.
Поставь скобки перед делением.
Сначала нужно раскрыть скобки посредство уножения одночлена на многочлен АХАХАХАХААХ ЧЛЕНЫ КАЖДЫЙ РАЗ СМЕШНЫ и только потом проводим деление, поэтому ответ 1
кто делает иначе - имбецилл
Хорошую вещь шарпом не назовут
Пересчитал в Бейсике на Xiao Ba Wang (эмулируется) и Google Gemini:
>Смотри: один двачер посчитал один и тот же пример 6÷2(1+2) на смартфоне и навороченном калькуляторе. На смартфоне результат 9, а на калькуляторе - 1. Я написал простенькую программу в Бейсике на Xiao Ba Wang, результат - 9.
Это классический пример «интернет-войн» вокруг порядка действий. Ты столкнулся с разницей между строгим математическим стандартом и специфическим правилом неявного умножения (multiplication by juxtaposition).
Вот почему результаты разошлись:
### 1. Почему получается 9 (Смартфон и Бейсик)
Это современный стандарт PEMDAS/BODMAS, который используется в большинстве школ и языков программирования.
1. Скобки: .
2. Выражение превращается в .
3. Слева направо: Деление и умножение имеют одинаковый приоритет.
В твоем коде на Бейсике ты явно написал `A/B(C+D)`. Для компьютера `/` и `` абсолютно равноправны, поэтому он просто идет по порядку слева направо.
### 2. Почему получается 1 (Калькулятор Sharp)
Многие инженерные калькуляторы (особенно старые модели Sharp и Casio) используют логику приоритета неявного умножения.
Они считают, что запись — это более «тесная» связь, чем . Согласно этой логике, умножение, записанное без знака, имеет более высокий приоритет, чем деление.
1. Скобки: .
2. Неявное умножение: Калькулятор видит как единый блок и вычисляет его первым: .
3. Деление: .
---
### Итог: кто прав?
С точки зрения современной алгебры и программирования: Прав смартфон и твой «Сюбор» (результат 9). Запись считается некорректно составленной именно из-за своей двусмысленности.
С точки зрения старых учебников и инженеров: Логика калькулятора (результат 1) тоже имеет право на жизнь, так как в некоторых старых правилах неявное умножение считалось приоритетным (например, часто трактуется как ).
Совет: Чтобы никогда не попадать в такую ситуацию, всегда ставь лишние скобки: либо `(6/2)(1+2)`, либо `6/(2(1+2))`.
Хочешь, разберем какой-нибудь еще «спорный» пример из учебников или программирования?
>Это современный стандарт PEMDAS/BODMAS
Когда ты начнешь работать с реальностью и такие вот дебильные хуйни с их дебильной хуйней про стандарты начнут тебе все портить тем, что твои конструкции начнут ломаться из-за хуевых рассчетов - тогда ты и поймёшь.
> Это то чему в школе учили, сначала делаются скобки. потом то что стоит рядом с ними без символа, а потом идёт действие с цифрой которая стоит после или до знака в сторонке
Не учили такому в школе.