32.
31.
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. http://arhivach.org/thread/109198/
30. http://arhivach.org/thread/114111/
31.
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. http://arhivach.org/thread/109198/
30. http://arhivach.org/thread/114111/
Зачем плодить одинаковые треды? Ты даун?
Шапка того треда просто ужасна.
Иди в тимфортрес поиграй, шапочник
На самом деле рли отсутствие ссылок на архивач - очень-очень плохо, хоть я ими никогда и не пользуюсь, но просто сама возможность проскроллить любой когда-либо существоваший тред греет душу :3
>3. Пусть A подмножество вещественной прямой. Верно ли, что не бывает такого, чтобы одновременно A имело нулевую меру и дополнение A было бы объединением счетного числа нигде не плотных?
Известный очень сюжет, я когда-то слышал название этому как: "теорема о колбасе: колбасу (отрезок [0..1]) можно разрезать на две части - невидимую (первой категории) и невесомую (меры 0)". Не думаю, что до той конструкции, что я знаю реально самому додуматься, но палить контору не буду, кто захочет - нагуглит.
Известный очень сюжет, я когда-то слышал название этому как: "теорема о колбасе: колбасу (отрезок [0..1]) можно разрезать на две части - невидимую (первой категории) и невесомую (меры 0)". Не думаю, что до той конструкции, что я знаю реально самому додуматься, но палить контору не буду, кто захочет - нагуглит.
>теорема о колбасе
Ох, как же я не люблю этот советский стиль юмора.
Справедливости ради, я самостоятельно эту задачку никогда не решал. Но смотря на известную мне конструкцию, мне кажется, что придумать этот контрпример можно просто здраво проанализировав определения этих двух понятий "быть маленьким множеством".
>1. Верно ли, что в каждом конечном графе имеются вершины одинаковой степени?
Да, степень каждой вершины не превышает n-1, где n число вершин графа. Следовательно согласно принципу Дирихле существуют минимум две вершины с равной степенью.
Примечание: необходимо чтобы граф был простым.
А ничего, что степени верши - числа от 0 до n-1 (т.е. n различных возможностей).
Контрпример.
Я не говорю, что заключение неверно, а указываю на дырку в доказательстве.
Каким образом факт, что степени вершин – числа от 0 до n-1 показывает на дыру в доказательстве? Возможностей кстати не n.
>Следовательно согласно принципу Дирихле существуют минимум две вершины с равной степенью.
Чтобы воспользоваться здесь принципом Дирихле нужно, чтобы возможных значений степеней вершин было бы меньше, чем самих вершин.
>Возможностей кстати не n.
Ну так докажи это и будет решение.
>Чтобы воспользоваться здесь принципом Дирихле нужно, чтобы возможных значений степеней вершин было бы меньше, чем самих вершин.
Вершин n. Степень каждой вершины v: d(v) ≤ n-1
>Степень каждой вершины v: d(v) ≤ n-1
Да. И это n возможных значений. Например, в графах на 4 вершинах могут встречаться вершины степени 0, 1, 2 и 3.
Верно, благодарю за замечание.
>Да, степень каждой вершины не превышает n-1, где n число
Предположим, что для любого v: 1 ≤ d(v) ≤ n-1 тогда утверждение доказано.
Иначе, существует вершина u т.ч. d(u) = 0.
Если она не единственная - утверждение доказано.
Иначе исключаем u и получаем n-1 вершин v, где 1 ≤ d(v) ≤ n-2 – согласно приниципу Дирихле существуют минимум две вершины с равной степенью. Утверждение доказано.
Берем вершину с самой большой степенью - предположим она равна N. Так как граф простой (для непростого графа утверждение неверно) то это вершина соединена с N другими вершинами. Так как вершин N+1 штука, а их степень может принимать значения от 1 до N - то как минимум две вершины имеют одинаковую степень.
Да, теперь в самом деле решение.
Изящнее.
Рассмотрим граф из n вершин. Если в графе есть две или более вершины степени 0, то все. Если такая вершина одна, имеем n - 1 вершин со степенью от 1 до n - 2. Если таких вершин нет, имеем n вершин со степенью от 1 до n - 1.
Че такое сопряжен, не напомнишь?
Хоть и не знаю, но полагаю, что решение 2й такое: g a g g b g = g a b g = g b a g = g b g g a g
Элемент $a$ сопряжен элементу $b$, если $a=gbg^{-1}$ для некоторого $g$.
1. https://arhivach.org/thread/18638/
2. https://arhivach.org/thread/27246/
3. https://arhivach.org/thread/27696/
4. https://arhivach.org/thread/38709/
5. https://arhivach.org/thread/46502/
6. https://arhivach.org/thread/48852/
7. https://arhivach.org/thread/52165/
8. https://arhivach.org/thread/56479/
9. https://arhivach.org/thread/63306/
10. https://arhivach.org/thread/70618/
11. https://arhivach.org/thread/74342/
12. https://arhivach.org/thread/74341/
13. https://arhivach.org/thread/76561/
14. https://arhivach.org/thread/78408/
15. https://arhivach.org/thread/79152/
16. https://arhivach.org/thread/82499/
17. https://arhivach.org/thread/92427/
18. https://arhivach.org/thread/84722/
19. https://arhivach.org/thread/87923/
20. https://arhivach.org/thread/91329/
21. http://arhivach.org/thread/93067/
22. https://arhivach.org/thread/94240/
23. https://arhivach.org/thread/95680/
24. https://arhivach.org/thread/96720/
25. https://arhivach.org/thread/99481/
26. https://arhivach.org/thread/100880/
27. https://arhivach.org/thread/101335/
28. http://arhivach.org/thread/106743/
29. http://arhivach.org/thread/109198/
30. http://arhivach.org/thread/114111/
31. https://arhivach.org/thread/116099/
32. https://arhivach.org/thread/118093/
Кто-нибудь ходит сюда?
http://ium.mccme.ru/f15/f15-krasilschik.html
На странице
http://www.mathnet.ru/php/conference.phtml?eventID=25&confid=763&option_lang=rus&if_videolibrary=1
последние две лекции отсутствуют, кому-нибудь известно, что что там было? и где можно посмотреть
http://ium.mccme.ru/f15/f15-krasilschik.html
На странице
http://www.mathnet.ru/php/conference.phtml?eventID=25&confid=763&option_lang=rus&if_videolibrary=1
последние две лекции отсутствуют, кому-нибудь известно, что что там было? и где можно посмотреть
>2. Верно ли, что если в конечной группе G выбрано подмножество A такое, что каждый g из G сопряжен некоторому a из A и элементы A попарно коммутируют, то G коммутативна?
Нет. Контрпример группа симметрий D_4:
D4 = {id, r1, r2, r3, fv, fh, fd, fc}
A = {id, r1}
Каждый элемент из D4 сопряжен с id из A,
id, r1 коммутируют, но D4 некоммутативна т.к. (например) r1 fv ≠ fvr1.
Единичный элемент не сопряжен никому кроме самого себя (в любой группе).
Да. Можно строить быстрорастущие функции из счетных ординалов с использование "быстрорастущей" иерархии https://en.wikipedia.org/wiki/Fast-growing_hierarchy . Стоит отметить, что скорость роста функции Аккермана достигается уже на $f_\omega(x)$ ($\omega$ наименьший бесконечный ординал, он соответствует порядковому типу натуральных чисел).
Приведенные выше функции, при некотором ограничение на ординалы, оказываются вычислимыми. Есть растущие еще быстрее, но уже невычислимые функции, например функция сопоставляющая натуральному числу $n$ наибольшее число с колмогоровской сложностью не превосходящей $n$.
Он в A, а значит условие
>каждый g из G сопряжен некоторому a из A
Выполняется.
Проблема в том, что это утверждение неверно
>Каждый элемент из D4 сопряжен с id из A,
Семинары в москве есть какие?
В Москве огромная куча математических семинаров. Тебя что конкретно интересует?
>Он в A
Не факт. A - это подмножество центра, а не центр.
Что сегодня будет.
Расскажите про программу Ленглендса. Говорят, в ВШЭ семинар про неё идёт.
Может ли это помочь физикам в их работах?
Может ли это помочь физикам в их работах?
Ты опять выходишь на связь, ебучий шакал?
Может быть здесь кто-нибудь ответит на мой вопрос в легитимном треде?
Тут больше гомологическую алгебру и спектральные последовательности знать надо.
Саентачи, что стоит почитать чтобы серьезно окунуться в теорию информации, теорию алгоритмов и кибернетику? Чтобы от начала (работы Тьюринга, Поста, Черча и других) и до современности И чтобы Лисп на Прологе в процессе написать. Бекграунд: хорошо знаю школьную математику, немного мат. анализ и дискретную математику.
Анон, реквестируй годный ресурс где поясняется за подстановки, перестановки, сигмы и всё с этим связанное доступным языком
У нас курса по группам не было да я зашкварок-прикладник. Так что хотелось бы советов с чего начинать обмазываться?
Я бы советовал начать с чтения учебника Винберга, заодно закроешь пробелы в других частях алгебры. Впрочем, я довольно далек от этих дел и наверняка здесь есть люди, которые могут дать более адекватный совет.
Почитай Вавилова "Конкретная теория групп".
Если это было для сообщения , то спасибо прочитаю. Есть еще что-нибудь, а то вряд-ли в 130 страниц (да и еще для направления бизнес-информатики) влезет много информации?
Начать скорее стоит со 2 части учебника Верещагина Шеня (вычислимые функции). Дальше можно переходить к более специализированным книгам по интересующим тебя темам.
Нашел, спасибо.
Ооокай
Объясните, как он к букету, цветку т.е., приклеил диск и получил сферу? Как приклеить диск к диску и получить сферу, вроде я могу представить, а здесь как это случилось?
Дело на самом деле пишет.
Аааа, а я думал это N-петух писал
ПидАРАСЫ лол КЕК ЫАХАХАХАХАХ сап двачь. лол ахахАХАХАХАХАХ КЕК КЕК
ЛОЛ
БЛЯ ПИЗДЕЦ Я ХЗ ВАЩЕ ЛОЛ
пидарыпидары пидарыпидары
>Summarizing:
> In wisdom there is no logic.
> In science logic often leads to the right result, but it cannot be trusted to so if its application is indefinitely repeated
> In mathematics it is uncertain whether the whole of logic is admissible and it is uncertain whether the problem of its admissibility is decidable.
> x-x-x-x-x-x-x-x-x-x-x-x-x-x-x
>Author's note to the 1919 reprint:
> This essay might be written to-day in the same form. The opinions which it defends have as yet not found many supporters
Классическая работа ОП-пика по философии математики. Коротко и хорошо объясняет интуиционизм.
> In wisdom there is no logic.
> In science logic often leads to the right result, but it cannot be trusted to so if its application is indefinitely repeated
> In mathematics it is uncertain whether the whole of logic is admissible and it is uncertain whether the problem of its admissibility is decidable.
> x-x-x-x-x-x-x-x-x-x-x-x-x-x-x
>Author's note to the 1919 reprint:
> This essay might be written to-day in the same form. The opinions which it defends have as yet not found many supporters
Классическая работа ОП-пика по философии математики. Коротко и хорошо объясняет интуиционизм.
Переклеивается всё - и лепестки все к друг другу, и диск на них ещё.
А, лепестки полностью друг к другу, а диск к ним по краю. Так?..
Да не, всё друг к другу.
Можно привести математическое доказательство тому, что конкретный человек говно?
Если принадлежит множеству человек следовательно говно. ЧТД.
Как вы считаете, среди математиков больше(или наоборот, меньше) поехавших в бытовом и психиатрическом смысле людей, чем среди остального населения? Есть ли связь между одаренностью в математике и "поехавшестью"(если формально, то наличием психических отклонений)/чудноватостью(формально - идиосинкразией)?
Есть корреляция. Но что является причиной чего - это вопрос.
Т.е. неизвестно едешь ли ты из-за математики или наоборот математика притягивает поехавших.
Какой-то математик говорил, что по статистике каждый 6й профессиональный матлогик имеет серьёзные проблемы с кукушкой. После лекций по теории сложности мне эта статистика не кажется такой уж необоснованной.
>После лекций по теории сложности
Хех. Теория сложности очень простая, если абсолютно измерять. В современных статьях есть гораздо более сложные теории всяких интересных вещей.
Это совершенно не мешает её преподавателю быть поехавшим.
А кто читал?
Я просто мимо проходил, не тот анон. Просто указал на небольшую логическую нестыковочку.
Ну ладно.
Тому анону, посещавшему курс сложности вычислений. Было бы любопытно узнать, что именно было не так с логиками?
Не знаю как у анона с сложностью, а у нас было два препода, один по алгебре постоянно улыбался, иногда повисал на лекциях на несколько минут и не мог себе никогда булочку или кофе в столовке купить, студентов просил. А второй книжку написал про связь с б-гом и про математический апокалипсис и анализ библии с позиции теории чисел и спрашивал на экзаменах не только по предмету, но и излюбенные цитаты из этой книжки.
Существует ли некоторая картофельная литература, главным содержанием которой являются примеры методов вычислений пределов, диффуров, интегралов и рядов?
http://www.alleng.ru/d/math-stud/math-st854.htm
http://www.alleng.ru/d/math/math148.htm
Ну и конечно же антидемидович.
В первый раз на этой доске. Недавно услышал от знакомого математика фразу "ультрафинитисты соснули, субъективный идеализм был прав". Что это обозначает? Я прочитал википедии про ультрафинитистов, но не понял связи с идеализмом.
>ультрафинитисты соснули, субъективный идеализм был прав
Блядь.
Ну серьезно.
Пробуй хоть чуууточку тоньше в следующий раз.
Ну про логиков это я от товарища математика, как раз слышал. Тот препод чьи лекции я слушал по сложности, как раз был 100/10, просто я физик и для меня все эти понятия типа разрешимости и перечислимости не очень-то естественные, в том смысле, что я из своей области не могу привести каких-то задач, где это может возникнуть, поэтому я и забил разбираться.
Ньюфаг выходит на связь.
Такой вопрос про вербитов учебник по топологии.
стр.165 он утверждает:
>Легко видеть, что в любой полной группе с инвариантной метрикой, заданной нормой ν, ряд вида Σgᵢ сходится, если сходится соотвествующий ряд из норм Σν(gᵢ).
Я правильно понимаю что он подразумевает под сходимостью суммы ряда сходимость фундаментальной последовательности составленной из частичных сумм согласно метрике группы?
Этот момент он просто не уточняет.
Такой вопрос про вербитов учебник по топологии.
стр.165 он утверждает:
>Легко видеть, что в любой полной группе с инвариантной метрикой, заданной нормой ν, ряд вида Σgᵢ сходится, если сходится соотвествующий ряд из норм Σν(gᵢ).
Я правильно понимаю что он подразумевает под сходимостью суммы ряда сходимость фундаментальной последовательности составленной из частичных сумм согласно метрике группы?
Этот момент он просто не уточняет.
Расскажите про программу Ленглендса. Говорят, в ВШЭ семинар про неё идёт.
Может ли это помочь физикам в их работах?
Может ли это помочь физикам в их работах?
Я не понял, хуле без N-петуха все вымерли?
Да.
Анон, помоги разобраться во второй части доказательства. Там говорится, что если e - еще один общий делитель, то общий делитель d из предыдущего абзаца делится на него. А с чего это вдруг он делится? Мы не накладывали ни на d, ни на e никаких ограничений кроме того, что евклидова норма d минимальная. То есть d может быть меньше e, и тогда e делится на d; d может быть больше e, тогда d в самом деле делится на e; они могут быть равны: d = e.
Откуда такой однозначный вывод?
Откуда такой однозначный вывод?
Несмотря на то, что полностью прав, отпишусь, тема то интересная.
Ультрафинитизм во всем хорош и правилен, единственная проблема, что он, при последовательном следование ему, приводит к удивительно скучной математике. Так что твой воображаемый знакомый совсем не прав, если это понимать, как то, что ультрафинитизм опровегли или что-то в таком духе и совершенно прав в том смысле, что субъективные идеалисты (ну или реалисты, если о том пошла речь) наслаждаются охуенно красивыми математическими абстракциями, пока ультрафинитисты экспериментально проверяют, определено ли значение 2^23.
Налажал со спойлерами.
Спасибо.
Там же явно написано, d = e * (сумма элементов). Вот отсюда
Как же у меня печёт анус жопы от лекция НМУ. Какого хуя сука нужно быть такими опущеными петухами чтобы записывать лекции без звука, с камерой спрятанной в жопе, обрезать лекции на середине или вообще забывать заливать файлики. Я в рот ебал этих пидорасов. Лучше бы они вообще лекции не писали, так хотябы не будет искушения.
А нахуя вообще желать лекции когда есть учебники? Тем более даже самая лучшая лекция это гнилой пересказ какого нибудь учебника.
Ну некоторые вещи лучше прослушать на самом деле. Сложные понятие типа предела или интегралов трудно почувствовать через сухое определения.
Ну я например жопу порвал об p-адические чилса, пока не почитал вики с определением "на пальцах". Часто книжки лишины данной части.
Во всех нормальных книжка перед формальными определениями есть мотивация или объяснение на пальцах. В любом случае, на лекциях я никогда не видел чего-то большего чем книгах.
>Ультрафинитизм во всем хорош и правилен, единственная проблема, что он, при последовательном следование ему, приводит к удивительно скучной математике.
Ультрафинитизм всем хорош, кроме того, что его не существует. Он не формализуется, в отличии от конструктивизма и интуиционизма.
Люди считающие себя ультрафинитистами есть, а ультрафинитизма нет, ну не смешно ли. Кстати, следуя твоей логике, у Брауэра не было никакого интуиционизма, а придумали его Гейтинг и Колмогоров.
Кстати забыл отметить, что даже само твое заявление об отсутствие формализации сомнительно. Скажем Эдвард Нельсон, насколько я понимаю, считал арифметику Робинсона Q приемлимой формальной системой.
Сап. Немного платины в этот тред.
Хочу немного продвинуться в математику. По профессии программист, в математике не полный кретин, естественно, но и не могу сказать, что разбираюсь хорошо.
Начиная с дифференциального счисления уже понятия не имею, что происходит в плане теории. Живу в 16 веке лол.
Короче говоря хотелось бы книжку, по которой можно нормально отследить идеи всего хардкора. В идеале хотелось бы начать с именно чтения, чтобы вкурить основные концепции и уже потом ебашить доказательства теорем и задачи.
Одновременно преследую две цели:
1. Расширить кругозор, ликвидировать пробелы в знаниях.
2. Получить базу для дальнейшего развития.
Хочу немного продвинуться в математику. По профессии программист, в математике не полный кретин, естественно, но и не могу сказать, что разбираюсь хорошо.
Начиная с дифференциального счисления уже понятия не имею, что происходит в плане теории. Живу в 16 веке лол.
Короче говоря хотелось бы книжку, по которой можно нормально отследить идеи всего хардкора. В идеале хотелось бы начать с именно чтения, чтобы вкурить основные концепции и уже потом ебашить доказательства теорем и задачи.
Одновременно преследую две цели:
1. Расширить кругозор, ликвидировать пробелы в знаниях.
2. Получить базу для дальнейшего развития.
Лектор может позволить себе привести хоть 10 аналогий и анекдотов, если видит непонимание. Книга же дает чтобы-нибудь одно, да и не факт, что это выстрелит.
К примеру алгоритм Евклида, объясняющийся традиционно через чрезвычайно "понятную" алгебраическую запись: а равно бэку нулёвое плюс эр один, бэ равно эродинкупервое плюс эр два, итд, можно представить в виде двух столбиков ебаных кубиков, что и сделает любой грамотный лектор, понимающий, что не все обладают хорошим алгебраическим мышлением.
У ультрасов даже натуральных числе нет.
Вспомнил N-петуха и проиграл, представляя, что таких людей, как он - много.
Хочу спросить людей, которые обучались на матмехе или просто очень хорошо знают математику.
Я учусь на физфаке, соответственно, владею математикой на уровне матфизики (тфкп и так далее). Включил курс "Группы и теория гомотопий" Романа Михайлова и просто охуел. Ну так же нельзя. Я понимаю большую часть того, что он говорит, но я понятия не имею ни о каких диэдрических группах.
Соответственно, как бы поднять теорию групп на должный уровень? Может, посоветует кто-нибудь учебник или задачник? Или просто хорошее чтиво. Курс этот я не потяну, кажется.
Ты - ПИЗДЛО.
Хотите чтобы N-петух вернулся? Могу это устроить.
Cогласен.
Не надо, пожалуйста. Все оппоненты ему уже проиграли в честном споре - сей факт запечатлен в архивах тредов.
so cute, я хочу
Ты не настоящий кнуёбок.
define настоящий
Если бы ты позволил отсосать свой хуй ты бы понял что я настоящий.
Ребята, давайте все вместе позовем N-петуха! N-ПЕ-ТУХ N-ПЕ-ТУХ N-ПЕ-ТУХ! Давайте все вместе ииии...
Была какая-то хорошая книга по теории групп для физиков, но я забыл ее название.
Действительнный.
А, ну тогда это точно я.
Вот это треш у вас в тредике. Ответьте по делу () котятки :3
Всё ровно так и есть.
Спешите видеть: N-петушара сам себе вылизывает анус в прямом эфире.
Ну у бога-петуха этого треда в его книжке, лишенной картафана, есть только формальное определение.
Предлагаю признать N-петуха эпичнейшей, легендарной личностью мат. тредов и увековечить его упоминанием в каждом ОП-посте. Как вы на это смотрите ребята? Правда же другого такого уже не будет! Осознайте это.
N-петушара, хватит заниматься аутофелляцией.
Прогерам обычно советуют кнутовскую "Конкретную математику". А так, боюсь, чтобы вьехать в современную науку, надо хотя бы пару лет поизучать университетский курс.
У меня есть как раз пара-тройка лет в запасе. Есть где-нибудь список литературы без картафана?
Я пытался читать конкретную математику, это пиздец уныло. При этом какую-нибудь топологию я могу весь день читать и не надоедает.
желательно на английском
http://habrahabr.ru/company/piter/blog/261469/
В этой книге я расскажу об одной из величайших идей, возникших в математике за последние пятьдесят лет, — программе Ленглендса, которую многие считают теорией Великого Объединения математики. Эта увлекательнейшая теория сплетает паутину глубоких связей между областями математики, которые, казалось бы, должны находиться на расстоянии световых лет друг от друга: алгеброй, геометрией, теорией чисел, анализом и квантовой физикой. Если представлять себе эти области как континенты тайного мира математики, то программа Ленглендса — это как бы такое телепортационное устройство, способное мгновенно переносить нас с одного континента на другой и обратно.
Так не читать, а решать надо. Читать смысла мало.
Слава N-петуху!
Не могу удержаться и не запостить ссылку на эту замечательную книгу.
http://www.math.miami.edu/~ec/book/book.pdf
Я давно думал, что можно посоветовать тому, кто совсем-совсем начинающий в «абстрактной» алгебре, да и математике вообще, и не мог ничего придумать (сам начинал не гладко). Есть много книг на каждую тему, есть ощутимое количество хороших книг и таких которые, содержат разные интересные/профессиональные аспекты, но эта меня впечатлила
1. Своим маленьким размером и простотой.
2. Идеологической правильностью.
Прошу прощения за претенциозность.
http://www.math.miami.edu/~ec/book/book.pdf
Я давно думал, что можно посоветовать тому, кто совсем-совсем начинающий в «абстрактной» алгебре, да и математике вообще, и не мог ничего придумать (сам начинал не гладко). Есть много книг на каждую тему, есть ощутимое количество хороших книг и таких которые, содержат разные интересные/профессиональные аспекты, но эта меня впечатлила
1. Своим маленьким размером и простотой.
2. Идеологической правильностью.
Прошу прощения за претенциозность.
Ну она и покрывает первые полгода институтского курса. Хотя книжка ОК.
Ты нихуя не понял ни доказательство, ни причину моего непонимания, и объяснять ты тоже не умеешь. Там сказано, что d и e - некоторые делители. И якобы d выражается через e. То есть все эти соотношения фиксированы.
Пусть d > e, например d = 8, e = 4. Тогда все верно.
Пусть d < e, d = 4, e = 8. И тогда уже d не выражается через e и та последняя формула неверна. Достаточно поменять местами значения d и e (формула остается неизменной), чтобы получилась ошибка.
[] ОБ ИЗВРАЩЕНИЯХ
~~~~~~~~~~~~~~~~~~
Вирмэйкерство -- это весьма молодая традиция; ведь для его развития
требуются умственные усилия, которые далеко не каждому по силам.
Прикиньте, сколько времени вы потратили на собственно разработку новых
вирусных технологий, не на свое обучение и написание вирусов функционально
идентичных уже существующим, а именно на нахождение нового знания. На
развитие вирмэйкерства потрачено всего несколько тысяч человекочасов.
Вирусная же сцена -- это мерзопакостная, впавшая в маразм старуха,
склоняющая молодое и чистое душой вирмэйкерство к отвратительному
сожительству.
Начинающие
Эти еще не определились, кем им стать. Пара недель на IRC, пара
"вирмэйкерских тусовок" (vx party). Часто вступают в какую-нибудь
"вирусную группу", а потом оттуда сваливают по причине "жизнь-такое
говно..." Большинство, к счастью, через короткое время исчезает.
Пиздюки
Наихудший вариант, в который переходят начинающие, ибо эти знают, "как
жить дальше". Они занимаются никчемными разговорами о вирусной сцене,
всегда и везде. Кидают очень много понтов и наезжают на начинающих.
Тормоза (вечно пишущие)
Следующая стадия после пиздюков. Эти на прямой вопрос о разработках
отвечают одну и ту же легенду: "пишем, скоро будет".
Рипперы
Стадия, параллельная тормозам, но более креативная. Их мало, но бывают.
Берется макро-вирус, изменяется/добавляется копирайт. Yeah!
Вирусоколлекторы (трэйдеры)
занимаются коллекционированием вирусов, троянцев, их описаний, исходников,
и прочей околовирусной ерунды, за деньги, просто так и в обмен на другие
вирусы. В частности, передают вирусы аверам.
Антивирусники (аверы)
занимаются продажей антивирусов, саморекламой и увеличением рынка "юзеров".
Бывшие вирмэйкеры
утратившие свою "потенцию", правда, обычно ее никогда и не имевшие, но это
не важно. Это старые, офигительно крутые чуваки; их ники можно встретить
абсолютно везде. Обычно у масс нет в них никаких сомнений. А зря.
Бывшие вирмэйкеры -- антивирусники
действительно кое-что хреновенькое написали (например .BAT-инфекторы),
но потом ссучились и решили заработать пару копеек своими
"профессиональными" знаниями. Они, как правило, несколько тупее
изначальных антивирусников. Иногда так и бросается в глаза
снисходительное, с их "высот" к нам "в низы", письмецо - типа, да, вот,
было время...
Комбинации вышеперечисленных
Здесь описаны лишь крайние стадии; на самом деле реальные люди
представляют из себя комбинации описанных направлений, например:
полурипперы-полупиздюки; полутормоза-полувирусоколлекторы.
[] КАК ЛЕЧИТЬСЯ
~~~~~~~~~~~~~~~~
Никак, да и не нужно это.
Истинные вирмэйкеры обладают пожизненным иммунитетом от вирусной сцены.
[] НУЖНА ЛИ ВИРУСНАЯ СЦЕНА
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Несомнено, да. Нужна. Нужна, ибо ее и так не существует для людей
правильных. Нужна, ибо попав в нее -- идиоты и кретины "от бога" -- там и
остаются, в результате чего легче подвергаются идентификации.
С другой стороны, посредством "сцены" легко найти требуемые вирусы, нужных
людей и документацию, что немаловажно для намеревающихся стать
вирмэйкерами.
[] РОССИЙСКАЯ ВИРУСНАЯ СЦЕНА
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Как сказал один мудрый человек,
- Уйдите, вы нам отвратительны.
Отягощенная национальным говнистым характером; бездействующая, абсолютно
пассивная; наезжающая на всех и вся; скучная, совершенно неинтересная;
деструктивная и злая в душе. И это -- в отличие от западной сцены, которая
мне, честно говоря, куда более приятна. Все дело в людях, друзья мои. На
убогом основании не вырасти умному человеку; злобный гопник никогда не
изменится. Исходя из этого, прогноз такой: в ближайшее время из
российской сцены "выйдут" намного меньше вирмэйкеров, чем из западной, а
значит на запад и следует ориентироваться в изысканиях нового знания и
распространении своих идей.
Розы не растут в помойке. Go West!
~~~~~~~~~~~~~~~~~~
Вирмэйкерство -- это весьма молодая традиция; ведь для его развития
требуются умственные усилия, которые далеко не каждому по силам.
Прикиньте, сколько времени вы потратили на собственно разработку новых
вирусных технологий, не на свое обучение и написание вирусов функционально
идентичных уже существующим, а именно на нахождение нового знания. На
развитие вирмэйкерства потрачено всего несколько тысяч человекочасов.
Вирусная же сцена -- это мерзопакостная, впавшая в маразм старуха,
склоняющая молодое и чистое душой вирмэйкерство к отвратительному
сожительству.
Начинающие
Эти еще не определились, кем им стать. Пара недель на IRC, пара
"вирмэйкерских тусовок" (vx party). Часто вступают в какую-нибудь
"вирусную группу", а потом оттуда сваливают по причине "жизнь-такое
говно..." Большинство, к счастью, через короткое время исчезает.
Пиздюки
Наихудший вариант, в который переходят начинающие, ибо эти знают, "как
жить дальше". Они занимаются никчемными разговорами о вирусной сцене,
всегда и везде. Кидают очень много понтов и наезжают на начинающих.
Тормоза (вечно пишущие)
Следующая стадия после пиздюков. Эти на прямой вопрос о разработках
отвечают одну и ту же легенду: "пишем, скоро будет".
Рипперы
Стадия, параллельная тормозам, но более креативная. Их мало, но бывают.
Берется макро-вирус, изменяется/добавляется копирайт. Yeah!
Вирусоколлекторы (трэйдеры)
занимаются коллекционированием вирусов, троянцев, их описаний, исходников,
и прочей околовирусной ерунды, за деньги, просто так и в обмен на другие
вирусы. В частности, передают вирусы аверам.
Антивирусники (аверы)
занимаются продажей антивирусов, саморекламой и увеличением рынка "юзеров".
Бывшие вирмэйкеры
утратившие свою "потенцию", правда, обычно ее никогда и не имевшие, но это
не важно. Это старые, офигительно крутые чуваки; их ники можно встретить
абсолютно везде. Обычно у масс нет в них никаких сомнений. А зря.
Бывшие вирмэйкеры -- антивирусники
действительно кое-что хреновенькое написали (например .BAT-инфекторы),
но потом ссучились и решили заработать пару копеек своими
"профессиональными" знаниями. Они, как правило, несколько тупее
изначальных антивирусников. Иногда так и бросается в глаза
снисходительное, с их "высот" к нам "в низы", письмецо - типа, да, вот,
было время...
Комбинации вышеперечисленных
Здесь описаны лишь крайние стадии; на самом деле реальные люди
представляют из себя комбинации описанных направлений, например:
полурипперы-полупиздюки; полутормоза-полувирусоколлекторы.
[] КАК ЛЕЧИТЬСЯ
~~~~~~~~~~~~~~~~
Никак, да и не нужно это.
Истинные вирмэйкеры обладают пожизненным иммунитетом от вирусной сцены.
[] НУЖНА ЛИ ВИРУСНАЯ СЦЕНА
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Несомнено, да. Нужна. Нужна, ибо ее и так не существует для людей
правильных. Нужна, ибо попав в нее -- идиоты и кретины "от бога" -- там и
остаются, в результате чего легче подвергаются идентификации.
С другой стороны, посредством "сцены" легко найти требуемые вирусы, нужных
людей и документацию, что немаловажно для намеревающихся стать
вирмэйкерами.
[] РОССИЙСКАЯ ВИРУСНАЯ СЦЕНА
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Как сказал один мудрый человек,
- Уйдите, вы нам отвратительны.
Отягощенная национальным говнистым характером; бездействующая, абсолютно
пассивная; наезжающая на всех и вся; скучная, совершенно неинтересная;
деструктивная и злая в душе. И это -- в отличие от западной сцены, которая
мне, честно говоря, куда более приятна. Все дело в людях, друзья мои. На
убогом основании не вырасти умному человеку; злобный гопник никогда не
изменится. Исходя из этого, прогноз такой: в ближайшее время из
российской сцены "выйдут" намного меньше вирмэйкеров, чем из западной, а
значит на запад и следует ориентироваться в изысканиях нового знания и
распространении своих идей.
Розы не растут в помойке. Go West!
За 5 лет общения с самыми разными "околовирусными" личностями, я
встречал людей, относивших себя к самой что ни есть вирусной сцене.
Несколько из них даже обладали минимальными способностями к исследованиям.
Большинство вирмэйкеров -- цивилы. Ни один не обладает в совокупной мере
возможностями и желанием что-то делать. Те, кто хотят -- не могут, а те,
кто могут -- не хотят. При этом наблюдается стойкое нежелание
объединиться; вместо этого они друг друга постоянно пытаются обосрать.
Никто не готов отдать _все_ за достижение своих, хоть каких-то, целей --
но даже не потому, что этих целей у них просто нет. Страх за свой жалкий
образ жизни и его смакование в разных формах занимают все время. Те, кто
хоть как-то развиваются, ограничиваются малым набором знаний, т.е. просто
программингом, и крайне редко чем-нибудь еще. Так что никто, даже
научившись многому (что само по себе нереально), не сможет это
использовать на полную, ибо кругозор ограничен экраном и местной курилкой.
Каждый имеет "хобби", а то и считает вирмэйкинг таковым; т.е. вирусы и
исследования не имеют для них решающего значения. Но ты либо гребешь изо
всех сил, не думая больше ни о чем, либо для виду подрыгивая конечностями
идешь ко дну. Нет никакой середины: или все, или ничего. Пытаться вместе с
этими (и всеми последующими) "вирмэйкерами" сделать что-то серьезное
вместе -- занятие абсолютно невозможное. Они будут "с тобой", вcе вместе и
по отдельности, но как только дойдет до дела -- ты окажешься один. И если
человек заявляет, что он вирмэйкер на всю жизнь (а такое бывает редко), то
это, скорее всего, не так. А если не заявляет, то и подавно. А зачем нужны
люди, которые за себя не отвечают, которые отнимают внимание и силы, а
взамен приносят разочарование? Жаль, что все это открывается лишь по
прошествии времени, когда уже поздно.
Наполовину прав был тот, кто говорил: в первую очередь -- моральные
качества, а все остальное потом; что сотрудничество возможно только с
твердыми, решительными, сильными, надежными и целеустремленными людьми.
Вторая же часть правды в том, что такие качества среди вирусной сцены,
увы, почти никогда не сочетаются со знаниями, и, обычно, чем больше
одного, тем меньше другого. А когда встречаются два человека, каждый
обладающий лишь одним из этих свойств, то они друг в друга не очень-то
верят. Вот это недоверие и лежит в основе всей сцены.
Ни одна "группа" не говорит: мы объединяемся, чтобы дополнить друг
друга, чтобы достичь того-то и того-то, и сделать то и то; ни один
"вирмэйкер" не знает точно, чего он хочет. А значит, им не к чему
стремиться; а кого не ждет впереди золотой кубок, тот бежит в пустоту.
Чтобы быть настоящим исследователем, надо бросить все остальное, без
исключения, абсолютно все. При этом вы должны быть полны надеждой и
стремлением; немного мозгов и везения тоже не помешают. И если ваше
упорство будет беспредельным, а помыслы совпадут с тем, что нужно миру
компьютеров, вы сольетесь с киберпространством, и знание придет и
останется с вами. Те, кто чувствовал это, поймут меня: вы оставляете
частичку своей души киберпространству, а часть его принимаете в себя; как
два порезанных пальца, приложенных друг к другу, вы теперь одной крови; и
в вас тоже горит бессмертный огонь, искра, что в силах зажечь этот мир.
Это чувство причастности к великому; особое мироощущение, которое делает
вас настоящим. Ищите же его!
встречал людей, относивших себя к самой что ни есть вирусной сцене.
Несколько из них даже обладали минимальными способностями к исследованиям.
Большинство вирмэйкеров -- цивилы. Ни один не обладает в совокупной мере
возможностями и желанием что-то делать. Те, кто хотят -- не могут, а те,
кто могут -- не хотят. При этом наблюдается стойкое нежелание
объединиться; вместо этого они друг друга постоянно пытаются обосрать.
Никто не готов отдать _все_ за достижение своих, хоть каких-то, целей --
но даже не потому, что этих целей у них просто нет. Страх за свой жалкий
образ жизни и его смакование в разных формах занимают все время. Те, кто
хоть как-то развиваются, ограничиваются малым набором знаний, т.е. просто
программингом, и крайне редко чем-нибудь еще. Так что никто, даже
научившись многому (что само по себе нереально), не сможет это
использовать на полную, ибо кругозор ограничен экраном и местной курилкой.
Каждый имеет "хобби", а то и считает вирмэйкинг таковым; т.е. вирусы и
исследования не имеют для них решающего значения. Но ты либо гребешь изо
всех сил, не думая больше ни о чем, либо для виду подрыгивая конечностями
идешь ко дну. Нет никакой середины: или все, или ничего. Пытаться вместе с
этими (и всеми последующими) "вирмэйкерами" сделать что-то серьезное
вместе -- занятие абсолютно невозможное. Они будут "с тобой", вcе вместе и
по отдельности, но как только дойдет до дела -- ты окажешься один. И если
человек заявляет, что он вирмэйкер на всю жизнь (а такое бывает редко), то
это, скорее всего, не так. А если не заявляет, то и подавно. А зачем нужны
люди, которые за себя не отвечают, которые отнимают внимание и силы, а
взамен приносят разочарование? Жаль, что все это открывается лишь по
прошествии времени, когда уже поздно.
Наполовину прав был тот, кто говорил: в первую очередь -- моральные
качества, а все остальное потом; что сотрудничество возможно только с
твердыми, решительными, сильными, надежными и целеустремленными людьми.
Вторая же часть правды в том, что такие качества среди вирусной сцены,
увы, почти никогда не сочетаются со знаниями, и, обычно, чем больше
одного, тем меньше другого. А когда встречаются два человека, каждый
обладающий лишь одним из этих свойств, то они друг в друга не очень-то
верят. Вот это недоверие и лежит в основе всей сцены.
Ни одна "группа" не говорит: мы объединяемся, чтобы дополнить друг
друга, чтобы достичь того-то и того-то, и сделать то и то; ни один
"вирмэйкер" не знает точно, чего он хочет. А значит, им не к чему
стремиться; а кого не ждет впереди золотой кубок, тот бежит в пустоту.
Чтобы быть настоящим исследователем, надо бросить все остальное, без
исключения, абсолютно все. При этом вы должны быть полны надеждой и
стремлением; немного мозгов и везения тоже не помешают. И если ваше
упорство будет беспредельным, а помыслы совпадут с тем, что нужно миру
компьютеров, вы сольетесь с киберпространством, и знание придет и
останется с вами. Те, кто чувствовал это, поймут меня: вы оставляете
частичку своей души киберпространству, а часть его принимаете в себя; как
два порезанных пальца, приложенных друг к другу, вы теперь одной крови; и
в вас тоже горит бессмертный огонь, искра, что в силах зажечь этот мир.
Это чувство причастности к великому; особое мироощущение, которое делает
вас настоящим. Ищите же его!
Ну это и подразумевается. Решать офк. Упражнения там унылое олимпиадное говно. Просто какие-то трюки идиотские надо делать.
Ну на самом деле у книги огромный недостаток, она при высокой сложности охватывает только какой-то базовый материал, уровня матшкольник 10 класс.
И зачем ты это говно принёс в тред по математике?
Видимо с точки зрения пылающего жопой гумуса, "вирусная сцена" и математическое сообщество - это "ну типа рядом".
Я бы еще поверил что "вирусная сцена" это харкач и этот итт тред, "вирусописатели" - это нормальные математики. Но если он под "вирусной сценой" видит всю математику - я к сожалению не могу осознать его обскурные пути мышления и цепочки ассоциаций.
>к сожалению
Или к счастью.
Ибо что взять с вшивого гумуса?
Пусть даны два топологических пространства $X$ и $Y$ и на них заданы некоторые топологии. Что имеется в виду, когда просят доказать, что $Y$ - подпространство $X$? Правильно ли я понимаю, что нужно показать, что данная топология $Y$ равна топологии $Y$ как подпространства $X$?
> Пусть даны два топологических пространства X и Y и на них заданы некоторые топологии
Про топологии можно было, конечно, не писать, но не суть.
Пусть даны множество X с данной на нём топологией и множество Y с данной на нём топологий.
Нужно доказать, что:
1. Y подмножество X.
2. Топология, индуцированная на Y из X, равна в теоретико-множественном смысле топологии, данной на Y в условии. То есть всякое множество, открытое в данной топологии, открыто и в индуцированной, и обратно.
http://hbpms.blogspot.co.uk/
Матаны, а вот эта программа норм или картафан?
Матаны, а вот эта программа норм или картафан?
Ясно, спасибо, ну я так и думал. Просто доказываю пикрелейтед в лоб, то есть доказываю, что
> Топология, индуцированная на Y из X, равна в теоретико-множественном смысле топологии, данной на Y в условии
и получается какое-то длинное муторное доказательство, хотя утверждение, казалось бы, очевидное. Я подумал, может есть какой-то более элегантный способ.
Если че, $J$ на пикрелейтед - это какой-то index set, по которому берется произведение.
Погоди-погоди, что-то я недопонял множества X и Y наделены структурой какого-какого пространства? Что-что на них задано?
Да, задано:
У меня те же самые чувства
Нет, там сказано, что d - это линейная комбинация элементов b_i (а не просто некоторый делитель), и отсюда всё следует. О том, что это так, что он действительно есть линейная комбинация b_i, рассказывается в первой части доказательства, которую, как ты утверждаешь, ты понял
вернее, я рассудил, что ты её понял, раз просишь разобраться именно во второй части
Ну что же вы, картафаны?
Первая часть: d - линейная комбинация b_i с наименьшей евклидовой нормой. Мы приходим к противоречию, когда предполагаем, что существует делитель меньший d, в этом случае евклидова норма этого делителя окажется меньше d, а это невозможно. Почему d делит все b_i? Ведь в этой линейной комбинации могли быть нули перед какими-то b_i, и тогда о делимости этих b_i с нулевыми коэффициентами ничего нельзя сказать.
Во второй части формула фиксирована. И если мы будем менять значения d и e как хотим, то в общем случае эта формула не верна. Это как если бы мы написали на си функцию, которая возвращает 0 или 1 при определенных значениях аргумента, и меняли эти аргументы местами.
Первый абзац: d - линейная комбинация b_i с наименьшей евклидовой нормой
Второй абзац: d - общий делитель b_i
Третий абзац: если e -другой делитель b_i, то d делится на e.
Вывод: d - наибольшей общий делитель
Во второй части формула фиксирована. И если мы будем менять значения d и e как хотим, то в общем случае эта формула не верна. Это как если бы мы написали на си функцию, которая возвращает 0 или 1 при определенных значениях аргумента, и меняли эти аргументы местами.
Слава N-петуху!
Чистмат мехмата МГУ
Т.е. картафан получается?
А то! Курс актуальный и прогрессивный для математики 60х годов, когда теоркат был "в новинку".
Хорошо, а где бы взять не картофанового курса?
Ну кроме вербитосоветов (у него со списком литературы туго).
мы не можем менять значение d, мы нашли d вполне однозначным выбором (наименьший элемент множества линейных комбинаций). поэтому d определён
Аноны! Поясните вотафак!?!
так когда дельту сокращаешь, дробь не переворачивается. На второй строчке ошибка
В шепутиарий.
на самом деле говорят нельзя частные производные считать как полные производные через производную обратной функции. вот только непонятно почему нельзя
Как зовут эту шизоняшу которая рассказывала про неделимость яблок в математике? Еще видео на ютубе часовые выкладывает.
Если r и x - координаты, то не надо переворачивать дробь. Чем быстрее изменяется первая координата при изменении второй, тем быстрее изменяется вторая координата при изменении первой — это интуитивно ясно. Геометрически это тоже понятно.
пздц
Вы правы.
Можно последнюю программу вербита для матфака посмотреть, там овердохуя литературы.
Где найти?
Там что-то у него с литераутрой не сильно лучше чем по каноничной ссылочке.
А вообще есть какая-нибудь программа на ингрише и без картафана?
Или вот например взять ту программку которую я выше кидал , выкинуть оттуда весь анализ нахуй (ибо в универе им меня уже накормили), что тогда получится?
>с литературой не сильно лучше
Ну я за всю жизнь не прочитаю, ты видно сильно способный.
Главное чтобы был выбор.
Если один учебник не идёт - хотелось бы иметь альтернативные опции из которых можно было бы выбрать.
Ну и опять же хотелось всё-таки учебнички на ингрише чтобы сразу привыкать к терминологии белых людей вместо птичьего языка пост-совка.
Пацаны, я вам задачу принес.
http://acm.timus.ru/problem.aspx?space=1&num=1013
http://acm.timus.ru/problem.aspx?space=1&num=1013
>Для практических целей, можно определить core mathematics как "предметы, которые используются в доказательстве теоремы Атьи-Зингера".
POOSHKA
Путин хорош на этой картине.
>4. Комбинаторика и теория множеств. Ликбез по общей математической грамотности: теоретико-множественный язык, аксиоматический метод, логика, комбинаторика.
>Литература.
>Дуглас Р. Хофстадтер. Гедель, Эшер, Бах: эта бесконечная гирлянда. Метафорическая фуга о разуме и машинах в духе Льюиса Кэрролла.
>...
>Ричард Ф.Фейнман. Вы, конечно, шутите, мистер Фейнман!
>...
>Энциклопедия элементарной математики (6 томов).
Это он траллит так?
Почему ты именно эти книги выделил? Остальные такие же развлекательные по сути.
Но бля какое отношение фейнман вообще к математике имеет?
Да просто хорошее чтиво. Там в книге много околоматематического.
Ну я могу вспомнить только момент когда он математиков троллил когда они ему рассказывали как из одного апельсина собрать два.
Да и в принципе, это же предназначается для учащихся в ВШЭ, там много полезного для студента, основанное на опыте самого Фейнмана.
> Если я правильно понимаю, ты видишь цикличность между 1 и 3?
Да. Плюс к этому, даже алфавит, еще до определения формул языка второго порядка, уже счетное множество.
> С "до" в данном случае согласен, с "независимо" нет.
Под зависимостью я имел ввиду только зависимость понятий. Если ты имеешь понятия A, B и хочешь дать определение новому понятию C и при его определении не опирался на A и B, то можно сказать что определение C является независимым от А и B.
Все что там сказано это типа мы просто будем использовать интуитиные понятия до их формального определения и ВСЁ. Почему это можно делать, там ни слова. Я же говорю, это просто плохой педагогический прием не имеющий ничего общего к систематическому построению математики. Это как в первом классе школоте объясняют что такое числа на всяких яблоках и их дележке и только через 5 лет дают некое подобие теории с доказательствами.
Верно ли, что если $A_{\alpha,\beta}$ - произвольные множества, то
$$\bigcup_{\beta \in K}\prod_{\alpha \in J} A_{\alpha,\beta} = \prod_{\alpha \in J} \bigcup_{\beta \in K} A_{\alpha,\beta}?$$
Я думаю, это так, потому что по определению декартова произведения каждое из этих множеств - это множество всех кортежей, у которых $\alpha$-я координата принадлежит хотя бы одному из $A_{\alpha,\beta}$. Я прав?
$$\bigcup_{\beta \in K}\prod_{\alpha \in J} A_{\alpha,\beta} = \prod_{\alpha \in J} \bigcup_{\beta \in K} A_{\alpha,\beta}?$$
Я думаю, это так, потому что по определению декартова произведения каждое из этих множеств - это множество всех кортежей, у которых $\alpha$-я координата принадлежит хотя бы одному из $A_{\alpha,\beta}$. Я прав?
Опять из под шконки вылез, шакал ебучий?
На форчан иди, дурачок.
Но меня там говном накормят. Я не хочу.
Если у тебя с этим какие-то проблемы, то потрудись изложить свои претензии.
Ну раз тебя даже там говном кормят, значит заслужил.
Эй, двачеватики, вы понимаете что все ваши графы, множества, гомологии и планиметрии, которые тип дохуя РАЗВЛИЧЕНИЕ ДЛЯ ИНТИЛЕКТА)) основанны на наблюдениях уровня "два камня плюс два камня будет раз...два...три...четыре....четыре камня"?
На клык захотел???
Ты хочешь сказать что все они основаны на натуральных числах, которые являются неопределямым понятием?
На форчане куда более добрая публика.
Подпесалсо.
Наверное ты говоришь о том же о чем и я, только по математически.
Я о том, что числа это абстракции основанные на наблюдаемыхз, реальных, физических объектах.
Подожди-подожди, а не замешана ли тут где-то метаиндукция?
Ты короче смотришь на объекты, но на самом деле это пиздеж, никаких объектов нет, ты не можешь думать о них, ведь используя индукцию ты по сути используешь ее саму, а так делать нельзя, должна же быть какая-то база....
То есть это содержательная метаиндукция на естественном языке?
Увы.
Но как я им объясню что такое картафан?
Метаиндуктивненько ты всосал
>Под зависимостью я имел ввиду только зависимость понятий. Если ты имеешь понятия A, B и хочешь дать определение новому понятию C и при его определении не опирался на A и B, то можно сказать что определение C является независимым от А и B.
В 1 использовалось понятие "индуктивное множество" (обозначим его A)
В 3 использовалось понятие "аксиома индукции" (обозначим его B)
Безусловно оба этих понятия ммм... "иллюстрируют" некий общий принцип под названием "индукция" (обозначим его C). Но, как говорится "есть нюансы" и нюансы эти существенны для построения в данном случае ФС. Цикличности здесь я не вижу. Здесь есть два независимых математических понятия, которые иллюстрируют принцип индукции.
Любую, даже самую бредовую, мысль можно сделать темой массовых обсуждений, если повторить её достаточное количество раз.
Ппц, мочерня уже фотки голых женщин трёт. Тут совсем детсад что ли???
> Здесь есть два независимых математических понятия, которые иллюстрируют принцип индукции.
Есть два понятия множества и совокупности, они независимы и иллюстритруют общую идею коллекции предметов.
Это неверная аналогия поскольку в первом случае понятие "индуктивное множество" является самостоятельным хорошо определённым математическим понятием со своим построением и со своим использованием, а во втором случае "аксиома индукции" - является аксиомой т.е. элементом ФС. То что оба этих объекта так или иначе "относятся" к общему понятию "индукция" не значит то что они ссылаются друг на друга. И тем более не являются синонимичными понятиями.
Таким образом, цикличности я здесь не вижу.
В твоём случае "множество", " совокупность", "коллекция" – это названия одного и того же причём матеиатическое определение имеет только 1-е.
Оплот целомудрия. Пшёл вон.
Как забавно у наших друзей из /бэ/ всё с ног на голову. Трут говнецо за фагами и подростками значит детсад, позволяют дегенератам постить своих негров и расчленёнку - нормальные взрослые люди.
>постить своих негров и расчленёнку - нормальные взрослые люди.
Именно так. Для высшего математического разума, который мыслит абстракциями, эти гомонегры и расчлененка ничего не значат. Это всего лишь способ дополнительно подчеркнуть направление мысли.
N-петух порвался, спешите видеть.
Это тебе мягко намекают под струю двигать, маня.
Называть любого, кто тебе не нравится N-петухом это проявление неуважения к настоящему N-петуху. Настоящий N-петух уникальная личность и очень умный человек. Не нужно порочить его имя.
>уникальная личность
Ага. Прям как переводчик. Наверное у N-петуха еще и зарплата большая.
Воеводский же обещает, что у него есть теория, которая изменит самые основания математики. Причём в такую сторону, что доказательства сможет проверять компьютер. Воеводский - это вам не какой-то хуй, он напридумал кучу теорий, за которые получил премию Филдса
Так что нахуй ваши метаиндукции и ваших петухов
Так что нахуй ваши метаиндукции и ваших петухов
С точки зрения мезантрапусов с двачей с довольно идиотской моралью - безусловно.
Все ваши "психологии", "морали" и прочие былопонятия для меня пустой звук. Реальны лишь только математико-логические абстракции. Все остальное (ты, я, вселенная, небо, аллах и др) это всего лишь отображения этих абстракций на поверхность гиперсферы нашего мира.
Почему гиперсферы?
> Все ваши "психологии", "морали" и прочие былопонятия для меня пустой звук.
Так почему наши-то? Это же ваша идея своё говно по всей борде разносить, /бэ/тардик.
А почему бы и нет?
потому что узнать в школе о том, что сферу можно нарисовать в 4хмерном пространстве, - это целое откровение!
Можно и в n-мерном. Но не нарисовать.
Основная проблемка такая: почему какая-то отдельная теоремка, нужная отнюдь не всем математикам возводится в асболют, и даже более того, всё что не используется в ёё доказательстве - предлагается не считать core mathematics?
Проверять доказательства компьютер уже может.
А вот любопытно, бесконечномерное пространство вообще имеет какой то математический смысл?
Оно даже физический смысл имеет. См. кванты.
>Ультрафинитизм во всем хорош и правилен, единственная проблема, что он, при последовательном следование ему, приводит к удивительно скучной математике.
А какую математику действительно можно построить с ультрафинитизмом? Понятно например сразу что какой-то серьёзной топологии или геометрии не может быть (хоть есть т.н. конечные геометрии - и там вроде даже что-то нетривиальное). А как будет выглядеть теория (конечных) групп с ультрафинитистской точки зрения, как думаете?
Матаны, напомните мне почему платноисты соснули?
Они не смогли дать определение натурального числа.
ну всякие гомотопии вроде как не может
Современная математика платонистская. Финитисты и прочие петухи соснули.
Потому что это красивая идея. И рассматривать надо не конкретные знание для теоремы, а области, в которые входят эти знания.
Явно описать Core Mathematics очень сложно, во всех известных перечислениях что-то упущено. Поэтому разумнее выбрать какую-нибудь теорему и определить coremath как всё, что требуется для её формулировки и доказательства. Конкретно теорема об индексе выбрана из эмпирических соображений. Опыт показал, что она абсолютно очевидна для тех, кто знает coremath, но у картофанов вызывает неконтролируемое воспламенение. Возможно, в будущем ситуация изменится, и вместо Атьи-Зингера будет какая-нибудь другая теорема.
>Конкретно теорема об индексе выбрана из эмпирических соображений. Опыт показал, что она абсолютно очевидна для тех, кто знает coremath, но у картофанов вызывает неконтролируемое воспламенение.
Ага, вот только это не определение coremath, ибо циклично завязано на то что coremath собственно считается. Если в качестве такой теоремы реальную проблему вычисления какого-нибудь дикого интеграла, то возгорание случится как раз у всяких алгебраических геометров, а людям специализирующимся на проблеме будет абсолютно очевидно например.
>только это не определение coremath, ибо циклично завязано на то что coremath собственно считается.
Ну тут никак не обойтись без метаиндукции!
Да что же это такое, математики совсем отупели, даже определить программу математики не могут!
Это адекватно описывает то, что понимают под coremath большинство людей, использующих этот термин.
Но скорее всего проблема вычисления какого-либо интеграла может быть сведена к алгебре, которой научить можно даже ребенка, без строгих определений и широких областей.
Интеграл по сравнению с высшей алгеброй дерьмо.
Меня вот что волнует последнии годы - уто и когда доказал логические операции НЕ, И, ИЛИ ведь если там кроется ошибка, то вся современная наука гроша ломанного не стоит
Меня вот что волнует последнии годы - уто и когда доказал логические операции НЕ, И, ИЛИ ведь если там кроется ошибка, то вся современная наука гроша ломанного не стоит
Великий английский учёный Буль, создатель алгебры Буля и собаки Буля (и, как частного её случая, терьера Буля).
Но ведь на булевой алгебре можно сконструировать N, а значит с твоих слов Гёдель ссыт Булю в лице.
Нет. Гёдель доказал, что логика предикатов непротиворечива и полна. Это так называемая теорема Гёделя о полноте.
https://ru.wikipedia.org/wiki/Теорема_Гёделя_о_полноте
В частности, полна теория Буля.
Чтобы сконструировать N, нужны значительно более мощные средства, чем просто логика.
>Чтобы сконструировать N, нужны значительно более мощные средства, чем просто логика.
Например метаиндукция.
Чтобы определить метаиндукцию, нужно иметь определение метаиндукции. Поэтому у метаиндукции нет определения. Всё, у чего нет определения, - бессмыслица. Поэтому метаиндукция - бессмыслица.
Вернёмся к открытиям Буля.
Нет, это не бессмыслица а исходное (неопределяемое) понятие.
Так, ну что с решением 2-й задачи из ОП-поста?
Ответ: нет, неверно.
Во-первых, ясно, что в качестве A всегда можно выбрать центр группы. Во-вторых, известно, что центр любой группы порядка p^n, где p - простое число, нетривиален, в тоже время, среди таких групп есть некоммутативные. Поэтому можно указать контрпример
>Это кукарек
Ясно. Как обычно.
И почему любой элемент сопряжён элементу из центра?
Не сопряжён. Рассуждение неверное
НЕПРИЯТНО детектед.
Самый быстрый способ найти 23х59 в уме?
Ответить 1357 без раздумий.
Берешь таблицу умножения и без задний мысли считаешь.
Эту задачу я взял из варианта вступительных экзаменов в аспирантуру матфака вышки за 2013 год. Из формулировки там ясно, что ответ положительный и что решение должно существенно использовать конечность группы (это был пункт а), а пункт б) той задачи про нахождения контрпримера для бесконечных групп). Я задачу решать не умею (алгебра определенно не мое сильное место), но учитывая общий уровень задач там думаю, что она должна быть вполне посильна для людей хорошо разбирающихся в алгебре на уровне бакалавриата того же матфака вышки. Исходя из общих соображений думаю, что задача связана с теоремами Силова, хотя сложно сказать однозначно. Было бы интересно самому узнать решение.
ОП
23x59 это 23x60 - 23. Мне кажется, так легче сосчитать.
Аноны, а сколько времени должно уходить на чтение учебника? К примеру, сколько времени нужно, чтобы вдумчиво, с нуля (ну не совсем с нуля, с небольшим бэкграундом) прочитать первый том Зорича? а сколько, чтобы прочитать оба? Нормально читать учебники по несколько месяцев? Читаете ли вы учебники? Если читаете, то сколько по времени и дочитываете ли до конца?
Прошу прощения за такое количество вопросов.
Прошу прощения за такое количество вопросов.
Ну вот так бы сразу.
Посоны, а sci-hub всё?
Я бы так считал:
23/2100=1150
2310-23=207
Это задача была еще и в листке первого курса, если что. И действительно не очень сложная. Для конечных рассмотрим действие группы на себе сопряжением и элемент из А, лежащий в самой большой орбите. Тогда его стабилизатор на размер орбиты равен количеству элементов в G, а с другой стороны не меньше количества орбит на размер самой большой. Но тогда все орбиты одноэлементны, так как есть единичный элемент. Для бесконечных вроде 2x2 матрицы с жнф в качестве А.
Моча пожалуйста не удаляй говно и гомонигру! Ведь свобода слова это очень круто! Будь хорошим человеком!
(Автор этого поста был предупрежден.)
Касательно конечных G, да как-то так, хотя лучше было бы написать решение подробнее, а не в одно предложение. Работает ли твой контрпример для бесконечных мне пока не ясно.
Да. Например, R является континуальномерным векторным пространством над Q.
Гораздо более интересен другой вопрос. Вот есть двойной интеграл, тройной интеграл, четверной интеграл, n-кратный интеграл. А есть ли бесконечно-кратный интеграл?
Интеграл Лебега в L² устроит?
Нет.
Можно ли начать изучать алгебру с известного учебника Ван дер Вардена? В целом, можно ли начинать изучение данного раздела математики напрямую с высшей алгебры, не касаясь материала школьного курса элементарной алгебры? Ведь, насколько мне известно, школьный курс рассматривает только частные вопросы общей алгебры. Так почему начать серьёзное изучение именно с последней?
У меня в среднем уходит от 30 до 60 минут на страницу.
Нет, ведь это же не бесконечно-кратный интеграл.
Там терминология устаревшая. Например, есть левые и правые векторные пространства. В наши дни под векторным пространством понимается исключительно модуль над полем, а эти объекты называются левый и правый модуль над телом. Поэтому лучше начать с какого-нибудь "Введения" Кострикина или с Винберга.
>Для бесконечных вроде 2x2 матрицы с жнф в качестве А.
Не все жнф матрицы 2x2 коммутируют.
Является ли истинным высказывание "для любого $a \in A$ выполняется $P(a)$", если $A$ пусто? По логике да. Но вот, например, 4.2 на пикрелейтед. Возьмем в качестве пространства $X$ множество целых чисел с метрикой $d(x, y) = |x - y|$. Тогда в таком пространстве нет ни одной сходящейся к $p$ последовательности такой, что $\forall n: p_n \neq p$.
Есть подозрение, что тут подразумевается, что $X$ такого, что любая окрестность (в данном случае окрестность - это шар), содержит бесконечное число точек. Есть какое-то специальное название для такого пространства?что для любой точки существует последовательность, сходящаяся к этой точке.
Есть подозрение, что тут подразумевается, что $X$ такого, что любая окрестность (в данном случае окрестность - это шар), содержит бесконечное число точек. Есть какое-то специальное название для такого пространства?что для любой точки существует последовательность, сходящаяся к этой точке.
На твоём скрине есть слово "limit point". В дискретной метрике нет предельных точек.
А все, понятно. Ну да, если $p$ - предельная точка, то понятно, что существует последовательность, сходящаяся к $p$.
Ну и у которой $p_n \neq p$.
У меня 20, только что проверил.
да, я знаю, что это очень легко решается и все такое, но, гайз, хелп ми плиз.
суть : нужно найти все такие значения параметра "а", что бы неравенство х^2-(3а-5)*х-а+(5/4) ≤ 0 , имело ровно 2 целых ответа, при этом оба отрицательных. Я понимаю, что это парабола, но на этом все.
суть : нужно найти все такие значения параметра "а", что бы неравенство х^2-(3а-5)*х-а+(5/4) ≤ 0 , имело ровно 2 целых ответа, при этом оба отрицательных. Я понимаю, что это парабола, но на этом все.
Нет, конечно нет. Пусть $\alpha=\beta=\omega$ и $A_{\alpha,\beta}$ попарно различные одноэлементные множества. Тогда $$|\bigcup_{\beta \in K}\prod_{\alpha \in J} A_{\alpha,\beta}|=\aleph_0,$$ но $$|\prod_{\alpha \in J} \bigcup_{\beta \in K} A_{\alpha,\beta}|=2^{\aleph_0}.$$
Получается, я проебался.
Твоя парабола должна пересекать прямую x = 0. Т.е дискриминант больше 0. Дальше расстояние между корнями должно быть больше или равно 1, но меньше 3 - чтобы между ними влезло ровно 2 корня. Только это не достаточное условие, потом надо будет перепроверить. Наконец, оба корня должны быть отрицательными. Составляет систему из этих условий, решаешь, потом перепроверяешь.
Поясните как из верхней формулы вышла нижняя.
Сложением всех уравнений сверху. Нахуй ты этим картофаном занимаешься? Норм подход такой: нужно заметить, что формула для $sum k^p$ - это многочлен степени $p + 1$. Вычисляешь эту сумму для $n$ от $1$ до $p + 2$, решаешь систему линейных уравнений относительно коэффициентов многочлена.
Кстати, это Спивак, да? Не читай эту хуйню, читай Рудина. Упражнения там по сложности такие же, но там хотя бы нет хуиллиарда ненужных упражнений и теория дается намного лучше.
>Сложением всех уравнений сверху.
Да, я не заметил там "and adding".
Да ладно, я после Спивака думаю Марсдена/Тромбу навернуть (векторный анализ), а потом Матан Апостола.
И то верно, что это за учёный такой, без собственного бизнеса, кому он нужен.
Давно хотел спросить, а диф.гем от спивака как? Такая же параша?
>Давно хотел спросить, а диф.гем от спивака как?
https://www.physicsforums.com/threads/a-comprehensive-introduction-to-differential-geometry-series-by-spivak.666556/
Анонче, помоги. Нихрена не понимаю.
Составить уравнение геометрического места точек, отношение расстояний которых до данной точки А(10,0) и до прямой х=12,5 равны числу К=4/5. Полученное уравнение привести к каноническому виду и построить кривую.
Уравнение вышло в итоге такое: 9x^2+100x-25y^2=0
А что делать дальше, как приводить к каноническому виду и строить - не ебу. Сотни нефти тому, кто поможет.
Составить уравнение геометрического места точек, отношение расстояний которых до данной точки А(10,0) и до прямой х=12,5 равны числу К=4/5. Полученное уравнение привести к каноническому виду и построить кривую.
Уравнение вышло в итоге такое: 9x^2+100x-25y^2=0
А что делать дальше, как приводить к каноническому виду и строить - не ебу. Сотни нефти тому, кто поможет.
Аноны, поясните, где на пикреле (если что, это Зорич) используется гладкость фи. Если следовать определению первообразной и доказывать прямым дифференцированием, то я не понимаю, где используется гладкость или зачем она там нужна. Я понимаю, что гладкость даёт непрерывность производной. Но зачем она здесь, если в определении от подынтегральной функции непрерывность не требуется, а для дифференцируемости композиции достаточно дифференцируемости обеих функций. Я понимаю, зачем требуется гладкость у определённого интеграла, но здесь что-то не могу уловить. Что я забыл?
φ'(t)dt
Хорошо. Тогда возникает такой вопрос. Пусть $X_\alpha$ - топологические пространства и $U$ - открытое подмножество $\prod_{\alpha\in J} X_\alpha$. Верно ли, что $U$ всегда имеет вид $U = \prod_{\alpha \in J} U_\alpha$, где $U_\alpha$ открыто в $X_\alpha$?
Все, понял, что хуйню сказал. Можно взять обычный круг на плоскости и это уже будет не так.
И что здесь даёт непрерывность? То, что можно будет написать dφ(t)? Так это и так можно будет сделать (хватит дифференцируемости). Можешь немного развернуть мысль?
Незадолго до сессии обнаружил что матан(тм) напрочь и успешно забыл.
Реквестирую способов за неделю или чуть больше ликвидировать неграмотность в школьном/первосеместровом калькулюсе.
Этого времени должно хватить чтобы вспомнить элементарные вещи, у меня все-таки не совсем нулевой левел.
Ключевые слова: непрерывность, ряды, сходимость, формула тейлора.
Толстые книги типа томов Зорича к сожалению не подойдут (нет времени), но если скажете конкретные главы/места которых должно хватить буду очень благодарен.
Реквестирую способов за неделю или чуть больше ликвидировать неграмотность в школьном/первосеместровом калькулюсе.
Этого времени должно хватить чтобы вспомнить элементарные вещи, у меня все-таки не совсем нулевой левел.
Ключевые слова: непрерывность, ряды, сходимость, формула тейлора.
Толстые книги типа томов Зорича к сожалению не подойдут (нет времени), но если скажете конкретные главы/места которых должно хватить буду очень благодарен.
Она не нужна, ты всё правильно понял.
Да, спасибо, я уже создал тему на dxdy. Сказали то же самое. Всё-таки иногда Зорич меня вводит в ступор. Я привык, что в математике стараются использовать как можно более слабые определения и как можно более общие выводы, но, когда без какой-либо мотивировки вводится сильное утверждение взамен слабого, я впадаю в ступор и начинаю нервничать, ибо возможны два варианта: 1) автор по наитию так сделал; 2) я что-то забыл или не понимаю. Наверно, мне не хватает уверенности.
>Я привык, что в математике стараются использовать как можно более слабые определения и как можно более общие выводы
Ну это не всегда так, далеко не всегда. Кстати, вот насчёт "дифференцируемых, но не непрерывно дифференцируемых функций" - пример хороший очень, дело в том, что никаких техник для тонкой работы с такими функциями нету. Вообще, если пример построен не искуственно, то никаких методов для доказательства того, что f - дифференцируемая, не доказывая при этом то, что f - непрерывно дифференцируема, кажется, тоже нету, об этом даже Тао говорил. А если техник для работы с ними нету, то зачем вообще на них внимание заострять? Никогда не задумывался, почему для множества "непрерывно-дифференцируемых функций на Х" ввели значок C^(1) (X), а для множества "просто дифференцируемых функций на Х" никакого общепринятого значка нету?
>Всё-таки иногда Зорич меня вводит в ступор.
Да у него много там "приколов" таких, когда он пытается наводить максимальную строгость, но прокалывается в некоторых тонких местах. Но мне кажется это не смертельно, лично я этот учебник люблю безмерно, как мой первый учебник по труъ математике, и всем его советую.
Ну это не всегда так, далеко не всегда. Кстати, вот насчёт "дифференцируемых, но не непрерывно дифференцируемых функций" - пример хороший очень, дело в том, что никаких техник для тонкой работы с такими функциями нету. Вообще, если пример построен не искуственно, то никаких методов для доказательства того, что f - дифференцируемая, не доказывая при этом то, что f - непрерывно дифференцируема, кажется, тоже нету, об этом даже Тао говорил. А если техник для работы с ними нету, то зачем вообще на них внимание заострять? Никогда не задумывался, почему для множества "непрерывно-дифференцируемых функций на Х" ввели значок C^(1) (X), а для множества "просто дифференцируемых функций на Х" никакого общепринятого значка нету?
>Всё-таки иногда Зорич меня вводит в ступор.
Да у него много там "приколов" таких, когда он пытается наводить максимальную строгость, но прокалывается в некоторых тонких местах. Но мне кажется это не смертельно, лично я этот учебник люблю безмерно, как мой первый учебник по труъ математике, и всем его советую.
мимо твой мемос, категориями я итак упарываюсь (хотя этот учебник кажется довольно уродливым)
мне бы теперь дифурчики и интегралы научиться брать
>А если техник для работы с ними нету, то зачем вообще на них внимание заострять?
Ну да, кажется, я понял. Дифференцируемость функции слишком общий случай, из которого «относительно мало» полезных свойств можно изъять. Так же как полугруппу наделают дополнительными свойствами и изучают её уже как группу. Хотя в том примере это не так уж важно. Главное, установить равенство, а чем более общий случай равенства мы можем установить, тем лучше.
>а для множества "просто дифференцируемых функций на Х" никакого общепринятого значка нету?
Видимо, потому что слишком общий случай, чтобы его выделять. Из дифференцируемости функции многого о ней не скажешь.
> лично я этот учебник люблю безмерно
Мне он тоже очень нравится, поэтому и читаю. Не всё гладко, конечно, но я могу сравнить только с устаревшим Фихтенгольцем (в лучшую сторону, естественно). А сколько времени, если не секрет, у тебя ушло на его чтение? Ну чтобы прямо так основательно, впитать каждую букву, а не просто пролистать. Да я тот анон, что спрашивал выше про чтение учебников.
Написал длинный пост, но случайно резетнул комп 3: Если коротко: то потратил я на учебник год, но только потому, что занятия математикой были бессистемны и "под настроение", а ещё я из-за своего перфекционизма зачем-то латехал решения всех упражнений, лил. Насколько эффективно для образования читать въедливо каждую букву не очень понятно. Оказалось, в итоге, что в Зориче математику нужно далеко не всё: в частности, по интегралу Римана можешь сильно не задрачиваться, всё равно в итоге придётся потом учить (если продолжишь занятия математикой) более простой и концептуально-правильный интеграл Лебега. Я бы на твоём месте почитывал бы параллельно учебник "Львовский "Лекции по математическому анализу"", не въедливо, но хотя бы просто по диагонали, чтобы узнать о том, как можно строить анализ по-другому, да и вообще некоторые вещи там интересны довольно. Таки дела.
Аноны, помогите с решением уравнения (x-2)(x-3)(x+4)(x+5)=1320 готовлюсь к олимпиаде (10 класс)
Используя метод Феррари, бета у меня получается равной -76, а в педевикии рассматривается только решение при бета = 0. Открыл первую страницу с задачами и, мягко говоря, охуел с их сложности, ведь такого в программе не было точно. Алсо, порекомендуйте учебник по алгебре на уровень 10-11 классов
Нид хэлп, срочно
Используя метод Феррари, бета у меня получается равной -76, а в педевикии рассматривается только решение при бета = 0. Открыл первую страницу с задачами и, мягко говоря, охуел с их сложности, ведь такого в программе не было точно. Алсо, порекомендуйте учебник по алгебре на уровень 10-11 классов
Нид хэлп, срочно
>Насколько эффективно для образования читать въедливо каждую букву не очень понятно.
Я это делаю потому, что не могу нормально двигаться в теории, пока не буду убеждён в обоснованности каждого действия, даже если интуитивно мне абсолютно всё понятно.
>по интегралу Римана можешь сильно не задрачиваться
Да я не задрачиваюсь, скорее изучаю, потому что до недавнего времени всё, что я знал о слове интеграл, было: «Ну это тип площадь под графиком.» Конечно, когда видишь чоткое определение, то многие теоремы, факты и свойства практически сразу становятся очевидными.
>всё равно в итоге придётся потом учить (если продолжишь занятия математикой) более простой и концептуально-правильный интеграл Лебега
Да, уже знаком с ним (примерно на том же уровне, что и с интегралом Римана до недавнего времени). Одно из первых действий, которые я сделал, взяв учебник Зорича, -- это поиск упоминания интеграла Лебега. Как оказалось, в Зориче его это как-то всё вскользь, но это не так уж проблематично.
За Львовского спасибо. Действительно очень занимательно.
Какой метод Феррари, ты поехал что ли? А если я дам тебе уравнение 5-й степени, что ты делать будешь?
Здесь совсем иной подход к решению задачи, она же "олимпиадная", а значит на соображалку. Хинт: разложи 1320 на простые множители.
Я не сильно могу в алгебрухоть и отличник, что вообще не показатель, и поэтому просто начал гуглить по уравнениям четвёртой степени, и наткнулся на это. А с разложением надо попробовать, да
Решил, всё нормально, спасибо за совет. Но разве нет другого выхода, кроме как подбирать корни?
Я думаю это самый оптимальный метод. Неужели подбор корней занимает так много времени? По-моему корень 6 вылазит прям сразу после разложения. Второй — после некоторых размышлений, которые так же не занимают много времени.
> Я это делаю потому, что не могу нормально двигаться в теории, пока не буду убеждён в обоснованности каждого действия, даже если интуитивно мне абсолютно всё понятно.
Тогда хотелось бы услышать как ты определяешь натуральное число???
>этот отступ
N-петух, скажи, а какая всё-таки у тебя зарплата? Большая?
Чуть выше средней по городу.
Я бы не хотел участвовать в этой демагогии просто потому, что не обладаю достаточными знаниями. Ну скажем, в Зориче даётся такое определение:
«Множество натуральных чисел — это наименьшее индуктивное множество, содержащее 1, т.е. пересечение всех индуктивных множеств, содержащих число 1.»
Как тебе такое определение?
>индуктивное
Пойду надену маску для защиты от жопной гари.
>индуктивное
Множество, которое содержит пустое множество и последователь любого своего элемента. По аксиоме бесконечности такие множества существуют.
N-петух помимо вербального засирания информационного пространства треда перешёл ещё и к визуальному? Чую скоро моча тебя банхаммером ёбнет и придётся тебе разбираться с натуральными числами самому.
Это что это? Больше десяти зёрнышек?
Matematiku neobyazatelno sovershenno znat classicheskogo analiza.
Ti voobshe ne matematik sooq, huli ti tut filosofstvuesh ))
Оно не является самостоятельным, ты не можешь осуществить его (индуктивного множества) построение без опоры на какую нибудь форму (интуитивной) индукции. Точно так же при описании формальной системы тебе требуется какая-то форма индукции (хотя конечно можно строить их независимо, но тогда придется предполагать исходными два вида индукции, что будет не нужным усложнением). Т.е. в этом смысле оба эти понятия основаны на какой-то интуитивной индукции, я в примере выше и обозначил ее С, а до этого называл метаиндукцией. Синонимичность в данном случае я не требую, это бессмысленно так как можно всегда искусственно разделить термины через какой нибудь частный случай или соглашение (типа одни считают N начинается с 0, другие с 1 или пример разделения на множества и классы). Но что действительно важно, это то что все эти формы индукции по сути эквивалентны.
Уже ёбнула?
ti che sooka ti che blyad tebe moi h-index pokasat? moi lekcii po algemu suka?! da menya sam shen uchel poka ti pod stol peshkom sral blyad! da ti uyebok ot prirodi suka pizdec ti menya vibesil chtoby zavtra vo dvore IUM bil suka v 18:00 posle seminara!
Твою мамку-шлюху ёбнули.
чем {0;2} отличается от [0;2]?
Мм, всем.
спасибо, я уже понял, извините за тупой вопрос
>Т.е. в этом смысле оба эти понятия основаны на какой-то интуитивной индукции, я в примере выше и обозначил ее С, а до этого называл метаиндукцией.
Согласен. Это в принципе то же что и я говорю:
>То что оба этих объекта так или иначе "относятся" к общему понятию "индукция"
Но вместо избыточного термина "метаиндукция", я использую общее понятие индукции. Но:
>не значит то что они ссылаются друг на друга.
И:
>Таким образом, цикличности я здесь не вижу.
Братишки нужна ваша помощь.
1) линеен ли оператор Ax(t)=sin(tx1) A:R^2 -> C(R)
2) придумать оператор A:C[0,1] -> C[0, +бесконечность)
1) линеен ли оператор Ax(t)=sin(tx1) A:R^2 -> C(R)
2) придумать оператор A:C[0,1] -> C[0, +бесконечность)
>Ax(t)=sin(tx1) A:R^2 -> C(R)
Я не очень понял, у тебя А зависит от двух параметров, однако, а формула t -> sin(t x) от одного.
Я не очень понял, у тебя А зависит от двух параметров, однако, а формула t -> sin(t x) от одного.
>2) придумать оператор A:C[0,1] -> C[0, +бесконечность)
0
0
в смысле оператор а применяется к функции x(t) sin(tx1) здесь t её аргумент, а x1 это первая координата точки R2 же
Значение x(t) принадлежит R2
>Значение x(t) принадлежит R2?
x(t) задана на плоскости
Так, процитируй условие задачи. Иначе тут разговор слепого с глухим получается.
С одной стороны A:R2 → C(R)
С другой: Ax(t) = sin(tx1) где 1 первая координата точки в R2.
Что это за точка? Это значение x(t) или нет?
Что значит t? Это одна переменная или вектор?
Пока условие неясно.
если x(t) задана в R2 значит t это вектор и t=(x1, x2)
В том то и дело, что условие задачи именно такое как я написал его сначала, препод дал задачи и нихера не объяснил, что есть что
> препод дал задачи и нихера не объяснил, что есть что
Видимо, он не думал, что ты даун и не можешь спросить, какая буква что означает?
>если x(t) задана в R2 значит t это вектор и t=(x1, x2)
это на иврите написано или на каком-то еще, неизвестном тебе, языке
Хватит обсуждать чью-то домашку. Лучше на ответьте.
Функциональный интеграл, он же интеграл по путям
Ну, короче, синус в любом из возможных случаев вряд ли линеен, так что отвечай так: "Нет, не линеен".
иди нахуй со своим картофелем
>иди нахуй со своим картофелем
Ну позязя, анончик, я весь вечер провозился с этой хуйнюшкой.
В ряд раскладывай все, что видишь.
Каледин, залогинься.
Забавно потому что вербицкий и подобные (как и любые матшкольники) все эти основы анализа, вплоть до простых дифуров и интегралов, узнали еще в старших классах
>она же "олимпиадная", а значит на стандартные методы решения "олимпиадных" задач
Пофиксил этого четвертьфиналиста.
Всегда проигрываю с этих дебилов, для которых операции уровня разложить четырехзначное число на множители и решить пару системок линейных уравнений это ОЛИМПИАДКИ СМЕКАЛОЧКА КОКОКО НИНУЖНО НАРМАЛЬНЫИ МАТИМАТИКИ ТАКОВА НИ ДАЛЖНЫ УМЕТЬ
двачую этого
в олимпиадных задачах нет ничего сверхъестественно олимпиадного, у составителей смекалочка не ахти как работает поэтому они просто юзают материал для следующего класса при составлении задач и не парятся. Ну по крайней мере так было, просто для проформы добавил.
>Открыл первую страницу с задачами
Че за книга? Можешь скинуть?
Ну вот ты и сам сказал, что в олимпиадных задачах нет ничего именно олимпиадного, т.е. отличного по духу от всего остального и неприменимого больше нигде. В учебничках к теме дают задачки - там нужно поюзать метод из темы, плюс немножко из пройденного. Задачки со звездочкой оттуда же - это помимо юзания метода еще и придумать, как его юзнуть. Олимпиадные задачки - это следующий этап после задачек со звездочкой: надо самому выбрать, какие методы юзать, и как. Этим же самым любой математик будет заниматься хотя бы при написании диссера - выбором методов и придумыванием, как и на чем их юзнуть, чтобы получить результат. Просто задачи будут глобальнее и методов будет больше, но один хуй этому учиться придется, если хочется чего-то достичь. Ну а неспособность осилить методы школьной/вузовской программы или пользоваться ими (что однохуйственно) сразу обо всем говорит.
Про материал для следующего класса ты совершенно не прав, между прочим. Задачи даются на ту школьную теорию, которая школьником такого-то класса пройдена. С затрагиванием вещей, которые обычным школьникам вообще не преподают - но в такой форме и в таком размере, чтобы они смогли это понять и решить.
>Про материал для следующего класса ты совершенно не прав, между прочим.
В теории давать задачи, требующие материал следующего класса, не комильфо. Но на самом деле все олимпиадники знают материал следующего класса. В этом соль олимпиадного ракования.
В соревнованихя по бегу в мешках побеждает не тот кто умеет хорошо бегать, а тот кто умеет хорошо бегать в мешках. В этом суть олимпиадного ракования.
>лично я этот учебник люблю безмерно, как мой первый учебник по труъ математике, и всем его советую.
Пиздец. Нахуй так жить.
В этом суть любого соревнования вообще: лучше в нем себя показывает тот, кто к нему готовился, чем тот, кто не готовился. ЕГЭ пишут лучше те, кто решал задачи для ЕГЭ, чем просто дохуя умный (потому что умный может где-нибудь обосраться со знаком, например). Новые результаты в области больше открывают поработавшие в этой области профессора, нежели просто залетные мамкины гении. Что сказать-то хотел?
Посоветуешь что-то лучше?
Нихуя они не открывают, это старое мудилы, "пробежать быстрее" - не значит "открыть новую дорогу".
То, что наверное анон хотел сказать - что ваши олимпиады имеют мало отношения к жизни реальной, когда во-первых тебе нередко нужно разбираться в хуйне, которую ты в первый раз видишь, а во-вторых проблемы часто вообще лежат в ненаучном русле, но задроты, коими является большинство "ученых" предпочитают вообще эту сферу игнорировать.
Есть ли символ, или как мне быть с разностью в количество раз между двумя числами? То есть, модуль разности двух чисел - их скалярная разность, на сколько два числа отличаются друг от друга, а вот что же сделать с двумя числами, которые не можешь просто разделить, так как не знаешь, кое из них наибольшее?
Посоветуйте учебник, где пошагово и полно излагается теория групп. Меня интересуют, в частности, группы Ли.
Никак не могу определиться, что по этому вопросу почитать.
Никак не могу определиться, что по этому вопросу почитать.
Выудил из этого треда учебник вавилова, так что остаётся только вторая половина вопроса - насчёт групп Ли.
Переформулируй вопрос.
Есть диффур du/dt + λu(t) + iwu(t) = eE/m, где u=dx/dt + i dy/dt, решением которого является функция u(t) = eE/m(λ+iw) + Cexp(-λt-iwt). Начальные условия (dx/dt, dy/dt) = (0, 0). Как найти здесь константу? Если взять u(t) = 0 и приравнять, то в итоге хуйня полная получается и зависимость от t пропадает.
>u(t) = eE/m(λ+iw) + Cexp(-λt-iwt)
0 = eE/m(λ+iw) + C
что тут не так? вроде норм, отсюда константа находится
Как сгенерировать все простые (без петель и кратных ребер) графы, состоящие из $n$, вершин с точностью до изоморфизма?
Господа, а поясните пожалуйста доходчиво, почему критикуется эпсилон-дельта формализм?
В нём используется метаиндукция.
Т.к. он всегда или почти всегда может быть заменен на более общий топологический.
Он труден для восприятия, неудобен в работе и может быть заменён более удобным и более общим формализмом фильтров.
Ну ты можешь считать, что окрестность точки p - это любое открытое множество, содержащее p (а не только шар, как в метрическом пространстве). Я не особо шарю, но мне кажется, есть смысл изучать топологию, если ты собираешься изучать какие-то неметризуемые топологические пространства (http://mathoverflow.net/questions/52032/examples-of-non-metrizable-spaces) либо просто из интереса. Метрическое пространство намного понятнее топологического и геометрическая интуиция там работает.
Увидел N-петуха в /pr/ и проиграл в голосяндру.
Ну так обосравшись тут он пошел в другие разделы
> обосравшись тут
Так N-петух приводил нормальные аргументы, просто определение N интересно только узкому кругу опущенцев.
Его аргументация сводилась к тому, что в определении N при помощи аксиом Пеано - присутствует цикличность. Неверно (видимо в силу недостатка знаний и опыта) интерпретируя понятия "индуктивное множество", "аксиома индукции" и оперируя общим понятием "индукция" (почему-то заменив его на метаиндукцию), он утверждал о цикличности.
В диалоге с ним: , я пытался показать, что цикличности здесь нет.
Да похуй, главное что не здесь.
>N-петух
Полчаса в пейнте, и он с нами!
Няш, доставь ему в тред в /pr/ вот это, пусть порадуется:
господа, подскажите годную литературу по теории игр
с меня печеньки
с меня печеньки
Ты до сих пор думаешь, что он искренне заблуждается, а не просто толсто троллирует?
Читай классику D&D
10/10
Наткнулся на сайт странного человека под именем Barry Dalgarno, и он либо поехавший, либо самый гениальный человек в мире. Пишет, что нашел закономерность в простых числах и даже как то ее описывает.
Основной текст: https://sites.google.com/site/geometryoftheprimes/
Карта сайта (сайт большой, навигация в принципе отсутствует) https://sites.google.com/site/geometryoftheprimes/system/app/pages/recentChanges
Картинки у него уж слишком красивые получаются, получше спирали Вильяма, но алгоритм построения лично я так и не понял. Возможно, просто я тупой.
Основной текст: https://sites.google.com/site/geometryoftheprimes/
Карта сайта (сайт большой, навигация в принципе отсутствует) https://sites.google.com/site/geometryoftheprimes/system/app/pages/recentChanges
Картинки у него уж слишком красивые получаются, получше спирали Вильяма, но алгоритм построения лично я так и не понял. Возможно, просто я тупой.
Серега Герасимов, опять ты?
Не знаю таких, кто это?
Такой гениальный, а в тех так и не научился.
Скорее всего. Но даже если это и троллинг, то своей цели он не достиг. Цель троллинга - раздражение, провоцирование агрессии. В процессе объяснения её не было (а это раздражает тролля). Это одна из тактик т.н. "backtrolling"-а.
Не задевайтесь словами. Что там по сути то?
|5-3| = |3-5|
волшебныйсимвол5/3волшебныйсимвол = волшебныйсимвол3/5волшебныйсимвол
Что за символ?
>А есть ли бесконечно-кратный интеграл?
Естественно, блядь. Определи его как предел последовательности.
мимо-любитель-картофанчика
Ты в "что где когда" играешь?
Лол, случайно зашёл в раздел в случайный тред и увидел свою руками переписанную копипасту аксиом Пеано.
Раз уж так сложилось, помогите мне: что у нас есть из дискретных ортогональных базисов, кроме Хаара (вейвлет) и Уолша-Адамара?
Формулировка задачи такая: у меня есть матрица n X n значений от 0 до n-1. n-значная логика от 2 переменных, говоря языком дискретки. Смотрю визуализацию этого дела и чую, что описать можно как-то просто. Но с Хааром и Уолшем-Адамаром обосрамшись, почти все коэффициенты не равны нулю и вообще выглядят как шум.
Сап, посоны. Ищу годные книги по формальной логике и математической логике. Был бы благодарен, если кто-то посоветует годную литру.
Вот есть идея: Обобщением преобразования Уолша является преобразование Виленкина — Крестенсона:
Используется при анализе и синтезе устройств автоматики с элементами, выполняющими операции троичной и q - ичной логики.
У меня как раз n-значная логика...
Кто-нибудь сталкивался?
Текущий уровень знаний логики и математической культуры в целом (школьникам и аспирантам математикам подходят совсем разные книги)?
> формальной логике и математической логике
Это по сути синонимы. А по теме, гугли книгу Э. Мендельсон Мат. логика
Я бы не рекомендовал. В качестве доступного учебника Верещагин Шень куда удачнее. На роль учебника более продвинутого уровня куда лучше подходит Шенфилд.
Всем похуй?
Есть ли математическое название/описание построения похожих листоподобных бесконечных фракталов?
Чтобы было понятнее, требуется это для построения бесконечной улицы. Поэтому особая "природность" не нужна.
Мне не похуй. Сразу же спиздил ссылку себе в текстовичок. Смущает то, что у него математический аппарат подробно не расписан. Я привык чтоб разжёвано было, а тут просто что-то типа Фибоначчи графически.
Где откопать матаппарат к картиночкам?
Можешь показать?
> Верещагин Шень куда удачнее.
Тупое говно которым даже подтереться нельзя так как оно в электронном виде.
Ну посмотри в любом учебнике, как определяется предел последовательности. Вот у тебя будет предел последовательностей рекурсивного взятия кратного интеграла. Даже задачку по матану такую помню, посчитать многомерный кратный интеграл.
Ты признал что в обоих случаях имеет место прямая зависимость от интуитивного понятия индукции, т.е. без нее данные понятия не существуют так как их попросту нельзя сконструировать.
Насчёт цикличности к которой ты прикопался, ок я соглашусь с тобой так как это абсолютно не принципиально в той формулировке которую ты используешь (я по старой памяти думал ты понимаешь аксиоматику Пеано в кнуёбковском смысле, т.е. как реальное определение N "из ничего").
Но ведь интеграл не обязан быть счётнократным. А предел по Гейне сработает максимум для континуально-кратного интеграла.
> Его аргументация сводилась к тому, что в определении N при помощи аксиом Пеано - присутствует цикличность.
Цикличность понятий не означает что они абсолютно тождественны, если пример с множествами не нравится, то смотри школьное определение точки например.
Я имел ввиду неустранимую зависимость от интуитивной индукции поскольку она является сутью натурального ряда, все остальное бантики.
Сап, хочу распознавать цифры. Вот отсюда я взял датасет:
https://www.kaggle.com/c/digit-recognizer/data
Если лень читать, то картинка представляет собой матрицу 28*28 из чисел от 0 до 255; чем темнее пиксель, тем больше число на соответствующей позиции.
Я решил сначала научиться отвечать на вопрос, является данная цифра единицей, или это что-то другое. Самое банальное решение: выход - линейная функция от всех входов, то есть каждый пиксель имеет какой-то вес $w_i$. Пытаюсь сделать градиентный спуск, но не получается. Формулу градиентного спуска я вывел следующим образом. Пусть у нас training set $T$ состоит из пар $(x, t)$, где $x$ - вход и $t$ - выход, который должен получиться. Воспользуемся методом наименьших квадратов. Суммарная ошибка равна
$$E = \frac{1}{2}\sum_{(x, t) \in T} (w^Tx - t)^2$$
$$\frac{\partial E}{\partial w_k} = \sum_{(x, t) \in T} (w^Tx - t)\frac{\partial(w^Tx - t)}{\partial w_k} = \sum_{(x, t) \in T} (w^Tx - t) x_k$$
Тогда на каждом шаге нужно изменять $w$ следующим образом:
$$w = w - \eta \sum_{(x, t) \in T} (w^Tx - t) x,$$
где для $n$-й итерации $\eta = с / n$. Я пробовал подбирать разные значения $c$, но проблема явно не в этом.
Вот код:
http://pastebin.com/F0g93bHF
Почему-то у меня некоторые веса становятся порядка 10^60. Я неправильно вывел формулу, или эту задачу нельзя решить градиентным спуском?
https://www.kaggle.com/c/digit-recognizer/data
Если лень читать, то картинка представляет собой матрицу 28*28 из чисел от 0 до 255; чем темнее пиксель, тем больше число на соответствующей позиции.
Я решил сначала научиться отвечать на вопрос, является данная цифра единицей, или это что-то другое. Самое банальное решение: выход - линейная функция от всех входов, то есть каждый пиксель имеет какой-то вес $w_i$. Пытаюсь сделать градиентный спуск, но не получается. Формулу градиентного спуска я вывел следующим образом. Пусть у нас training set $T$ состоит из пар $(x, t)$, где $x$ - вход и $t$ - выход, который должен получиться. Воспользуемся методом наименьших квадратов. Суммарная ошибка равна
$$E = \frac{1}{2}\sum_{(x, t) \in T} (w^Tx - t)^2$$
$$\frac{\partial E}{\partial w_k} = \sum_{(x, t) \in T} (w^Tx - t)\frac{\partial(w^Tx - t)}{\partial w_k} = \sum_{(x, t) \in T} (w^Tx - t) x_k$$
Тогда на каждом шаге нужно изменять $w$ следующим образом:
$$w = w - \eta \sum_{(x, t) \in T} (w^Tx - t) x,$$
где для $n$-й итерации $\eta = с / n$. Я пробовал подбирать разные значения $c$, но проблема явно не в этом.
Вот код:
http://pastebin.com/F0g93bHF
Почему-то у меня некоторые веса становятся порядка 10^60. Я неправильно вывел формулу, или эту задачу нельзя решить градиентным спуском?
Я то ли в маразм впал, то ли не понимаю твоих трудностей.
a_n при n-> +inf
где n -- кол-во кратностей интеграла. Счётное, как и нужно
Ну и рекурсивно задаётся a_n = _/ a_{n-1} dx
Пусть n - какой-то ординал.
Нужно определить ∫n. Если n - конечный ординал, то всё очевидно. Если n = ω, то интеграл очевидно определяется так, как ты сказал. Но как быть, если n > ω? У меня есть подозрение, что теория меры меня обломает.
В нем обходятся многие тонкости, но ровно это и делает его хорошим учебником для людей с низким уровнем предварительной подготовки. Кстати, он несколько раз переиздавался и его должно быть легко купить.
Вообще, похоже тебе нужно то, что обычно называется замощение, только с фракталами.
Вот из первых ссылок, что выдаёт по этому запросу:
https://en.wikipedia.org/wiki/Pinwheel_tiling
https://en.wikipedia.org/wiki/Aperiodic_tiling
Покопай в эту сторону.
L-systems же.
Все пацаны, отбой, ошибка была в коде.
Какие тонкости?
>Ты признал что в обоих случаях имеет место прямая зависимость от интуитивного понятия индукции, т.е. без нее данные понятия не существуют так как их попросту нельзя сконструировать.
Не знаю что ты называешь "прямой зависимостью", но без интуитивного понимания индукции, на одной формализации действительно далеко не уедешь. Также как без интуитивного понимания точки или предела последовательности. Но строгость в математике требует формального определения понятий, и оно было дано в логике второго порядка.
>Насчёт цикличности к которой ты прикопался, ок я соглашусь с тобой
Так.
>так как это абсолютно не принципиально в той формулировке которую ты используешь
Не принципиально для чего?
>Я имел ввиду неустранимую зависимость от интуитивной индукции
Так.
>поскольку она является сутью натурального ряда,
Что это значит?
>все остальное бантики.
Ты извини, но как известно "the devil in the details". Если ты формальную систему построенную как индуктивное множество, в которой присутствует аксиома индукции, если ты всю эту конструкцию несущую определённую информацию в областях математики и играющую важную роль в доказательствах называешь "бантиками", то это лишь показывает, что ты не видишь значения определения, и не ориентируешься в этих областях, пытаясь только интуитивно понять этот объект и попадая в ловушку собственной интуиции, ошибочно утверждая о "замкнутом круге".
> Не знаю что ты называешь "прямой зависимостью"
Я же сразу после ближайшей запятой пояснил что я имею ввиду.
> но без интуитивного понимания индукции, на одной формализации действительно далеко не уедешь.
До формализма ты даже не дойдешь, ты его без индукции построить не сможешь.
> Также как без интуитивного понимания точки или предела последовательности.
Ты похоже вообще ничего не понял. Речь не про интуитивные образы помогающие понять или найти решение, а про исходные понятия без которых невозможно сконструировать простейшие вещи вроде формальной системы. Для геометрии как раз интуитивного представления о точке не требуется если есть система формальных аксиом. Как говорил Гильберт вместо точек могут быть пивные бутылки. Для натуральных чисел так не получится потому, что избавиться от интуитивного представления об индукции при построении аксиоматики Пеано невозможно.
> и оно было дано в логике второго порядка.
Логика второго порядка требует пререквизита в виде индукции.
> Не принципиально для чего?
Для того чтобы утверждать об неустранимости интуитивной индукции на которой всё строится (меня устраивает такая более слабая формулировка). Иначе ты будешь пытаться отрицать наличие цикличности на основе каких-то своих представления о ней.
> Что это значит?
Натуральный ряд это какой-то единичный объект к которому применена индукция. Первое совсем тривиально, второе является самым главным в конструкции натурального ряда. Поэтому говоря об определении N главный акцент делаем на индукции.
> если ты всю эту конструкцию несущую определённую информацию в областях математики и играющую важную роль в доказательствах называешь "бантиками"
Мы обсуждаем только корректное определение N, это же не повод изучать 500-страничное доказательство теоремы Ферма например?
помоги
ЭТА НАУКА
@
ТА НАУКА
@
СПОСОБ ПРО ЭТО ДУМАТЬ
@
ЖИВЁТ
@
БЬЁТ
@
УВАЖАЕТ
@
ТА НАУКА
@
СПОСОБ ПРО ЭТО ДУМАТЬ
@
ЖИВЁТ
@
БЬЁТ
@
УВАЖАЕТ
Ну-ка бамп.
Сайт не читал. На картиночках нихуя не простые числа.
Ребят, есть тут люди, занимающиеся машинным обучением, анализом данных, мат. моделированием или чем-то в том же духе? Честно прогуливал в универе все математические дисциплины, теперь вот не знаю, куда обратиться.
Допустим, у нас есть истории клиентов, которые пользовались определённой услугой, содержащие определённые действия по дням.
Задача: построить такую модель, которая, приняв на вход данные юзера, который ещё не перестал пользоваться услугой, спрогнозировала бы, сколько он продержится.
Вопрос в том, как правильно собрать пространство признаков, объясняющих количество дней активности?
Дней много, возможных действий тоже много, так что строить таблицу со столбцами вида
день1_действиеА;день1_действиеБ;день1_действиеВ ... день47_действиеХ;день47_действиеЦ;день67_действиеЧ;
- не самый лучший выбор (но пока единственный из пришедших мне в голову), к тому же матрица получится не только растянутой, но и разряженной за счёт большого количества пользователей, которые продержались только пару дней.
Как вообще решаются такие задачи и как они правильно называются, в какую сторону копать и что гуглить?
Допустим, у нас есть истории клиентов, которые пользовались определённой услугой, содержащие определённые действия по дням.
Задача: построить такую модель, которая, приняв на вход данные юзера, который ещё не перестал пользоваться услугой, спрогнозировала бы, сколько он продержится.
Вопрос в том, как правильно собрать пространство признаков, объясняющих количество дней активности?
Дней много, возможных действий тоже много, так что строить таблицу со столбцами вида
день1_действиеА;день1_действиеБ;день1_действиеВ ... день47_действиеХ;день47_действиеЦ;день67_действиеЧ;
- не самый лучший выбор (но пока единственный из пришедших мне в голову), к тому же матрица получится не только растянутой, но и разряженной за счёт большого количества пользователей, которые продержались только пару дней.
Как вообще решаются такие задачи и как они правильно называются, в какую сторону копать и что гуглить?
БЛЯ, НЕ СЛУШАЙ ЭТИХ ДОЛБАЕБОВ. ТУТ НАДО УМНОЖИТЬ 1Ю СКОБКУ НА 3Ю, А 2Ю НА 4Ю. ЗАТЕМ ЗАМЕНА t = x^2 + 2.ПИЗДЕЦ ТУТ ДАУНЫ СИДЯТ
t = x^2 + 2x. ОПИСАЛСЯ
Можно интегрировать по пространству функций
Нормализация данных, feature selection.
Суть кратного интеграла в том, что его можно свести к повторному.
>Ребят, есть тут люди, занимающиеся машинным обучением, анализом данных, мат. моделированием или чем-то в том же духе?
Я иногда занимаюсь.
>Вопрос в том, как правильно собрать пространство признаков, объясняющих количество дней активности?
В общем случае никто не скажет, нужно делить модель на training и validation множества и тестировать, визуализировать, тестировать еще раз. Можно погуглить статьи с похожими подходами.
Далее, если данных у тебя много, ты можешь использовать продвинутые методы, если мало - придется очень долго заниматься manual feature selection. Чем меньше данных, тем больше дроча и шаманства. В твоем магазине данных, скорее всего, мало.
>но и разряженной за счёт большого количества пользователей, которые продержались только пару дней.
Выкинь первую колонку, а правую добей ее нулями, чтобы у каждого пользователя вектор был одной длины (большой), соответствующий состоянию пользователя в день N (без пропусков) и попробуй кластеризовать это многомерное пространство с визуализацией на 2d (через PCA, например). Возможно, тебе получится разбить пользователей на большие кластеры и работать с кластерами по-разному (типа, если юзер сделал больше 3-х действий, переводим его на другой алгоритм).
Далее, по сути, ты действие каждого пользователя можешь закодировать в виде некоторого процесса перехода из состояния в состояние (в виде или моего плоского вектора, или твоей "сжатой" таблички). Т.е. в день N у тебя пользователь находится в состоянии A, на следующий день с вероятностью P он может перейти в состояние B. А это значит, ты можешь использовать reccurent neural network, которой на вход подаются данные о новом дне (или состояние + дельта дней), а она каждый раз пытается угадать, что сделает юзер с учетом истории его действий.
Из всего числового ряда строишь матрицу Ганкеля, затем подсовываешь ее любому алгоритму без учителя (SOM, NG, GNG, ...). На готовую модель проецируешь новые данные и смотришь к какому кластеру она их отнесет.
Окей сведи мне интеграл по пространству непрерывных функций на отрезке (0,1) к повторному.
Я пытаюсь понять, возможно ли это.
А вот поясните за пикрелейтед интеграл. Как его представить наглядно? D - размерность, для простоты можно считать = 1.
Бля ты шутишь что ли, давай ты пояснишь за обозначения, что откуда, куда. Ибо для меня E - это может быть энергия, напряженность электрического поля и.т.д
Это из векторного квантования. Е - ошибка квантования, P(v) - плотность вероятности распределения, v - вектор вещественнозначных чисел, wi(v) - тоже вектор вещественнозначных чисел такой же размерности что и v (скажем v - точка кластера, тогда w - центроид этого кластера), выражение (v - wi(v))^2 - это евклидово расстояние между v и w соответственно (т.е. между точкой кластера и центром этого же кластера). Т.е. по отдельности все просто и понятно, но интеграл, как в этом случае он выглядит, как его нарисовать - в душе не ебу.
с теорией информации не знаком, но интеграл до ужаса напоминает дисперсию случайной величины( или что тоже самое, что второй момент случайной величины)
>интеграл до ужаса напоминает дисперсию случайной величины
Ну да, суть примерно в том же - разброс отдельных точек кластера относительно центра в пределах плотности вероятности, только вместо матожидания случайной величины координаты центра кластера, а в качестве случайной величины - координаты элементов кластера. Но все равно непонятно, как нарисовать такой интеграл.
Математики, почему логарифм единицы пл\о основанию десять равен 0?
лолбля. сорри. я все вспомнил.
Что-то вы меня совсем запутали. Картофаны - это прикладники или «чистые».
Гротендики вроде тоже водяру любят.
Кстати, вербит же злостный бурбакист.
Гротендики вроде тоже водяру любят.
Кстати, вербит же злостный бурбакист.
Картофаны это вторая культура.
Первая -- построение теорий, (пример -- формализм пучков, язык схем, теорема об индексе); вторая -- решение конкретных задач (пример -- комбинаторика, общая топология и функциональный анализ, cs, олимпиадная математика). Для первой теорема всегда важнее доказательства, а определение важнее теоремы, в идеальном случае там все должно вытекать из определения. Так это изложено у Гауэрса. Вербицкий называет это "core mathematics" и периферия. Гауэрс же настаивает на том, что комбинаторные результаты нередко устанавливают связь между различными ветвями и направлениями математики. Но с точки зрения Вербицкого эти направления одинаково неинтересны, поскольку относятся к "прикладной науке". И т.д.
Конкретно МГУ ближе к второй культуре, потому что там такая идеология. Для них важнейшей ценностью является количество курсов в программе, сокращать её они не готовы, и таким образом включение туда современной математики (многообразия и дифференциальные формы, когерентные пучки и классы черна, теорема римана-роха в форме гротендика) сделает невозможным освоение программы студентами. То есть, там и так студент должен знать, чем интеграл Макшейна отличается от интеграла Курцвейля-Хенстока; поскольку это соответствует специалисту широкого профиля, в понимании мехмата.
Смысл концептуального подхода в том, что он радикально упрощает математику путем введения нового, более удобного языка. См, например, формулировку уравнений Максвелла в терминах дифференциальных форм. Трудность, в этом случае, состоит только в освоении этого самого концептуального аппарата, т.е. заучивании определений и осознании их фактического содержания.
Вторая культура это поиск более элегантных доказательств, первая -- более элегантных формулировок. Вторая культура увеличивает объем математического знания, первая -- его сжимает.
Существует опасность того, что математических работ станет настолько много, что их перестанут читать, и придется передоказывать каждое утверждение десятки раз.
Вербицкий отнюдь не бурбакист. Вообще, трактат Бурбаки имеет мало общего с первокультурной математикой и создан скорее как некоторого рода формальная система, или как пример, иллюстрирующий возможность построения такой системы. Алгебраическая геометрия is nowhere near.
Вербицкий же конкретно занимается гиперкэлеровыми многообразиями и пишет учебники по метрической и римановой геометрии.
>Гротендики вроде тоже водяру любят.
Откуда ты это взял, хуй знает.
Poconi, как побороть математическую прокрастинацию? Вроде и тема качает, и знаю что понравится если втянусь, но лень начинать вообще, что-то читать, разбираться.
> Алгебраическая геометрия is nowhere nea
Как же бесит эта уебанская манера школодаунов вставлять неуместные английские слова.
> Откуда ты это взял, хуй знает.
Читай его биографию, он же в деревне спился под конец жизни.
Ну так в этом вся суть выебывающихся школьников
Последовательность {X_n} имеет предел при n -> inf. Пусть {Y_n} -- это "перемешанная" последовательность {X_n} (т.е. y_n = f(n), f: N -> X_n). Верно ли, что они тоже сходится?
>Вообще, трактат Бурбаки имеет мало общего с первокультурной математикой
На самом деле довольно много. Но кто читал, тот и так знает, а остальные не поймут.
Да, разумеется. Последовательность имеет пределом точку A - значит, в любой окрестности A лежат почти все точки последовательности. Если изменить номера точек, сами точки ведь не сдвинутся, как лежали почти все, так и будут лежать.
ты что у нас тут каждый школьник - первокультурщик, двигающий теорию пучков и состоящий в AMS
Если ты рандомно переставишь элементы и эту перестановку нельзя выразить аналитически, то нет, т.к нельзя будет указать окрестность для определенного номера(она не будет выполнять условие |x-x_n|<e)
Спасибо, немного упростил себе задачу и вручную разделил юзеров по активности, а в качестве целевой переменной поставил интервалы. Не так красиво, зато понятно и в целом тоже работает.
Теперь другой вопрос: как искать аномалии во временных рядах? Допустим, у нас тот же датасет в формате день_время;юзерайди;действие;сумма_оплаты;платежная_система
Ряд не стационарен и со временем показатели растут.
Задача построить такую модельку, которая бы искала вбросы по одному или нескольким признакам (допустим, в какой-то день неожиданно много оплат в ночные часы по одной из платежных систем).
Вопрос может и глупый, но я впервые сталкиваюсь с задачами прогнозирования и временными рядами, до этого препарировал только результирующие таблицы, где внутренняя динамика признака была не важна.
Что у нас тут будет объектом: юзер или день, а что его признаками? Словом, в какой вид нужно нарезать исходные данные и как такие задачит вообще принято решать?
Из понятного гугл советует только эту статью:
http://habrahabr.ru/post/251225/
Но тут в качестве данных не ряд, а та же результирующая таблица.
Буду очень благодарен за совет.
Лол. Перестановка последовательности - это любая биекция N->N. Достаточно "аналитически" для тебя?
Поддвачну этого. Можно добавить, что "почти все" означает "все кроме конечного множества точек".
Пацаны, важно ли, чтобы кто-то проверял доказательства, которые я пишу, когда читаю учебник, или главное - это развить интуицию, а если доказательство содержит ошибку - то похуй? Просто вот я прочитал формулировку теоремы, доказал ее, потом читаю доказательство в учебнике, а оно не такое, как у меня. После этого я внимательно перепроверил свое доказательство, но все равно есть шанс, что я ошибся.
Второй вопрос: кто-то постил свои доказательства или решения задач на math.stackexchange для верификации? Как там к такому относятся? У меня с ангельским норм, потому что я погромист, но я как-то стесняюсь. Знакомых, с которыми можно скооперироваться нет, потому что я не математик и живу в Мухосранске. Если че, занимаюсь энтрилевельной математикой типа линала, матана и общей топологии.
Второй вопрос: кто-то постил свои доказательства или решения задач на math.stackexchange для верификации? Как там к такому относятся? У меня с ангельским норм, потому что я погромист, но я как-то стесняюсь. Знакомых, с которыми можно скооперироваться нет, потому что я не математик и живу в Мухосранске. Если че, занимаюсь энтрилевельной математикой типа линала, матана и общей топологии.
>Задача построить такую модельку, которая бы искала вбросы по одному или нескольким признакам (допустим, в какой-то день неожиданно много оплат в ночные часы по одной из платежных систем).
Вот сейчас смотрю насчт временных рядов, ARIMA, автоматический подбор параметров, все дела: https://www.google.ru/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&cad=rja&uact=8&ved=0CB4QFjAAahUKEwj8vrCC2pLJAhXnnXIKHQXVDkY&url=http%3A%2F%2Fwww.jstatsoft.org%2Farticle%2Fview%2Fv027i03%2Fv27i03.pdf&usg=AFQjCNF9MBsC7olXZ1Y55K01bzD2vuzE2g&sig2=waZlm5sbv6s_gO8Vh3ZsFg хуйня полная, предсказание на 10 шагов вперед, ошибка на тестовой выборке просто запредельная:
accuracy(forecast(fit,10), a[201:209])
ME RMSE MAE MPE MAPE MASE ACF1
Training set 0.008689936 1.006038 0.782161 -0.000381481 1.303290 0.9951399 -0.002189017
Test set -1.462308612 3.207413 1.652199 -2.512794011 2.800512 2.1020849 NA
и визуально "предсказание" выглядит как говно. Временные ряды не причем, это задача идентификации модели системы, причем должна быть достаточная выборка, один выброс уровня "допустим, в какой-то день неожиданно много оплат в ночные часы по одной из платежных систем" останется незамеченным.
Пруф ассистанты используй.
>Пацаны, важно ли, чтобы кто-то проверял доказательства, которые я пишу, когда читаю учебник, или главное - это развить интуицию, а если доказательство содержит ошибку - то похуй?
Главное - это получить правильную интуицию и научиться самому доводить свои доказательства до такого уровня строгости, когда ошибки весьма маловероятны. Поэтому, хотя нет ничего плохого, когда (относительно) быстро читаешь математические тексты и пропускаешь многие доказательства, придумывая общие схемы для пропущенных доказательств, и разумеется время от времени допуская ошибки, но для развития второго навыка видимо на первых порах действительно нужно чтобы доказательства проверяли.
Правда конкретно ничего не могу посоветовать - я учился в матшколе и после нее проблем с тем, чтобы при необходимости аккуратно записать доказательство у меня уже не было.
Про ариму и её варианты только слышал, но серьёзно не читал.
Выборка предостаточная есть, чувствительность к отклонениям, уверен, тоже можно будет настроить.
Я до сих пор не могу сообразить, как для таких задач должна выгледеть объект-признаковая матрица, ведь у нас есть и юзеры и их действия и платёжные системы и цены оплат и всё это взаимосвязано и продолжается во времени.
То есть каждое событие скаждого дня нужно проверять не только на то, выбивается ли оно из событий этого дня, но и насколько оно продолжает тенденцию предыдущих дней.
1. Что у нас тут объект, что признак, а что целевая переменная?
2. Какие инструменты (желательно, присутствующие в sklearn) могут понадобиться, чтобы чтобы решить задачу максимально просто, без претензии на запредельную точность и сложность применяемых методов?
Вопрос не совсем по математике, но я просто уже устал и не знаю где спросить. Как в LaTeX принято записывать остаток от деления? А именно, как записать
a = (b * c) % d
a = b \cdot c \mod{d}
или
a = (b \cdot c) \mod{d}
или как вообще принято, может как-то вообще иначе? Или киньте в меня зарубежными публикациями.
a = (b * c) % d
a = b \cdot c \mod{d}
или
a = (b \cdot c) \mod{d}
или как вообще принято, может как-то вообще иначе? Или киньте в меня зарубежными публикациями.
Я бы написал так
$a=bc \mod d$
$a=bc \mod d$
Анон, посоветуй книжку про арифметику в модулях. Как решать квадратные уравнения?
Ага, только у меня там всё сложнее. Произведение сложных обозначений / остаток от сложного обозначения.
Идите нахуй со своим машинным бучением в CS тред. Нехуя тут тему засирать.
Сам нашёл. Буржуи почему-то пишут вот так:
>b \cdot c ≡ a \pmod{d}
И я не понимаю, почему они пишут тождество (= вообще не ставят). Я вот доказываю утверждение от противного, и мне тоже тождество ставить? Чтобы доказать. что оно неверно.
Поясните за топологию. На вики пишут что там ей не интересны метрические подробности. Какая там математика используется? Примеры кто то может привести? Или там одно воображение, бесмысленное и беспощадное, а математика на подсосе чтобы другому человеку можно было объснить что ты там напридумывал без размахивания руками?
Но ведь это математика.
Как бы вы планарный граф в четыре цвета покрасили без комплюктера, а, матаны?
Вас какая топология интересует, молодой человек?
Самая что ни на есть общая, в которой пространство скрученное в бублик изучают и прочая прочая самая самая общая топология.
Так, не разжигаем, /cs необитаема, малоизвестна и, судя по всему, вообще закрыта, а задачи машинного обучения - частный случай прикладной математики.
Я всё ещё надеюсь, что знающие люди подскажут, в каком направлении решать эту задачу .
А вот поясните за бурбакизм, например. Конкретно за пикрелейтед выражение. Как именно там получается, что вся эта хуеверть определяет пустое множество?
Она не "определяет" пустое множество, а является им.
Ну, пусть является. Каким образом-то, в чем суть этого выражения? В самой книге объяснения нет.
Ты привык, что каждый набор символов означает какой-то объект. Здесь не так. "Значения" у этого набора символов нет. Он самобытен, самодостаточен. Пустое множество - это не "то, что обозначено набором символов, пустое множество - это и есть набор символов.
То есть, например, "собака" - это буквы с, о, б, а, к, а, записанные рядом друг с другом слева направо.
>это не "то, что обозначено набором символов"
fxd
Бурбакизм даже определение натурального чила не даёт, не много ли ты от него хочешь?
Дзен какой-то. Я понимаю, что в бурбакизме буква это буква, за которой не обязано стоять что-то кроме этой буквы. Мне смысл этого выражения не понятен.
>определение натурального чила не даёт,
Вот ты и пришел. И кстати, бурбакизм дает определение нуля и единицы, для остального достаточно аксиом Пеано.
Почему именно этот набор символов?
> для остального достаточно аксиом Пеано.
С точки зрения малолетнего долбоёба - безусловно.
Аксиомы Пеано определяют натуральные числа. Как и https://2ch.hk/sci/src/308111/14476738910610.jpg этот пик вполне определяет тебя. Поскольку кукареканья ничего не доказывают, а "математика" есть синоним "доказательства", предлагаю тебе привести пример хоть одного натурального числа, не вписывающегося в аксиомы Пеано.
Этот набор символов может быть осмыслен, но этот смысл не рассматривается бурбаками. Если бы метаматематика изучала собак, то она бы изучала правила построения текстов, содержащих слово "собака", и совсем не интересовалась бы смыслом слова "собака". Рассматривается лишь синтаксис, не семантика.
Вообще же, если интересоваться и семантикой, то философская суть такова.
Есть вещи, и есть утверждения о вещах.
И то, и другое обозначается наборами символов.
Эти наборы символов будем называть строками.
Строку, обозначающую вещь, назовём объект.
Строку, обозначающую утверждение, назовём высказывание.
Рассмотрим специальные символы, например +, - и ∈.
По смыслу, специальные символы - это либо какие-то операции, либо какие-то избранные предикаты.
Каждый специальный символ связывает два объекта.
Мы будем пользоваться прямой польской нотацией.
То есть, например, не будем писать a+b, а вместо этого будем писать + a b.
Специальные символы разделим на субстантивные и реляционные.
Субстантивные символы - это +, - и т.п.
Реляционные символы - это =, ∈ и т.п.
Если s - субстантивный символ, то s a b - объект.
Если s - реляционный символ, то s a b - высказывание.
Например, 5 и 7 - объекты.
+ 5 7 - объект.
= 5 7 - высказывание (ложное).
= + 5 7 12 - высказывание (истинное).
Кроме того, рассмотрим специальный эпсилон-оператор Гильберта (будем обозначать его буквой тау).
Суть такова.
Пусть P - какое-то высказывание.
P обозначает какое-то утверждение о вещах.
Одна из вещей, участвующих в P, может быть обозначена символом x.
τxP - это одна из вещей, которые подходят под утверждение.
Например, рассмотрим высказывание = x 7.
τx = x 7 - это объект, который обозначает вещь реального мира, которая находится в отношении, обозначенным =, с вещью, обозначенной как 7, - если такая вещь существует, в противном случае этот объект не обозначает ничего.
Например, τx= x 7 обозначает 7, потому что только 7 = 7.
В случае неоднозначности эпсилон-оператор делает выбор абсолютно произвольно.
τx ВЛАДЕЕТ (x, Сосач) обозначает Абу.
τx ЗАЕБАЛ(x, сцай) обозначает либо N-петуха, либо переводчика, но мы не знаем, кого.
τx ЖИВЁТВ(x, Россия) обозначает одного из жителей России.
Лол, малолетний долбоёб пыхтел два часа над дебильной картинкой которая никому не нужна, теперь как опущенный бегает по всему сосачу со своей фотокарточкой.
Пизданись, мудило. Почитай для начало что значит дать корректное определение понятию, а потом вопросы задавай. Кстати, даже если предположить что я такой пример привести не смогу, это НИЧЕГО не докажет так как из противоречивого высказывания можно вывести все что угодно. Пуанкаре сто лет назад угорал с таких даунов как ты, почитай может поймешь чего.
Конкретно тот набор символов можно, опуская двойное отрицание, переписать вот так.
∅ =def τy ∉τx∈xyy.
То есть пустое множество - это такая вещь, которая может стоять на месте y в высказывании ∉τx∈xyy.
Если от польской записи перейти к обычной скобочной, то это такой y, что (τxx∈y) ∉ y.
Символ τxx∈y обозначает одну из тех вещей, которые являются элементами y.
Если таких вещей несколько - одну из них, мы не знаем, какую.
То есть пустое множество - это такой y, что один из его элементов не является его элементом.
> Какая там математика используется?
Ты имеешь в виду, что нужно знать, чтобы начать изучать топологию? Ну вот я недавно начал. По-моему для общей топологии не нужно ничего, кроме теории множеств и определенного уровня математической культуры, чтобы не охуеть.
Боги математики объясните простыми словами что такое многообразие, перечитал тысячи определений в различной литературы, но полного, и главное, понятного представления так и не сложилось
>эпсилон-оператор Гильберта (будем обозначать его буквой тау).
А, ну это уже лучше. У бурбаков, кстати, про эпсилон Гильберта ничего не сказано.
Так действительно понятнее, спс.
>даже если предположить что я такой пример привести не смогу, это НИЧЕГО не докажет
Пок-пок, ваши пруфи не пруфи, вы все врети. Мань, это как раз однозначно докажет, что ты обосрался, причем себе же на ротешник. Ибо, если нет примеров натурального числа, не соответствующего аксиомам Пеано, то значит эти аксиомы исчерпывающе определяют N. Что в свою очередь подтверждает что твои кукареканья - это всего лишь кукареканья.
> что значит дать корректное определение понятию,
Опять же, если лично тебе что-то в математике непонятно, то это проблема твоя а не математики. Определение - это то, что исчерпывающе определяет что-то. В случае натуральных чисел определением являются аксиомы Пеано. А теперь съеби.
> Ибо, если нет примеров натурального числа, не соответствующего аксиомам Пеано, то значит эти аксиомы исчерпывающе определяют N.
Ебанько, чтобы задать этот вопрос тебе нужно cначала построить аксиоматику Пеано, а ты этого сделать не можешь без индукции, которая суть N. Соснул?
> Опять же, если лично тебе что-то в математике непонятно, то это проблема твоя а не математики.
Не путай свои представления малограмотного дебила с математикой.
> Определение - это то, что исчерпывающе определяет что-то.
Аксиоматика Пеано таковой не является так как содержит порочный круг.
> В случае натуральных чисел определением являются аксиомы Пеано.
С точки зрения мудака - безусловно.
>Аксиоматика Пеано таковой не является
Потому что ты так сказал? Я ж тебе предлагаю это доказать, т.е. привести пример натурального числа, не определяющегося аксиомами Пеано. Насколько я понимаю, это невозможно не только для поехавшего с подтирача, а для математики вообще. Что в свою очередь доказывает, что аксиомы Пеано определяют N. Определение же единицы есть у бурбаков.
Заебали. Лучше тут machine learning обсуждать, эту Санта-Барбару в виде N-петух vs. весь мир.
Ты необучаемый.
Сначала определим локально евклидово пространство размерности n.
Пусть M - хаусдорфово пространство.
Путь в нём есть открытые связные подмножества.
Пусть некоторые из них гомеоморфны открытым подмножествам Rn.
Пару (U, f), где U - открытое связное подмножество M, а f - гомеоморфизм на Rn, будем называть картой.
Причём f будем называть координатным отображением.
Пусть (Ui, fi) - семейство карт такое, что Ui образуют покрытие M (т.е. их объединение равно M).
Тогда такое семейство называется топологическим атласом.
M с топологическим атласом называется локально евклидовым пространством размерности n.
То есть локально евклидово пространство размерности n - это хаусдорфово пространство, каждая точка которого обладает окрестностью, гомеоморфной Rn. Топологическое многообразие - это синоним локально евклидова пространства.
Теперь определим дифференциальное многообразие.
Пусть есть две карты (U,f) и (V,g).
Так как f и g - гомеоморфизмы, у них есть обратные гомеоморфизмы f-1 и g-1.
Отображение f∘g-1 будем называть отображением склейки.
Отображение склейки - это гомеоморфизм открытых подмножеств Rn.
Значит, для отображения склейки определено понятие производной.
То есть отображения склейки могут принадлежать каким-то классам гладкости.
Пусть есть топологическое многообразие размерности n.
Пусть его атлас таков, что у любых двух карт отображение склейки относится к классу Ck.
Тогда атлас будем называть дифференциальным атласом класса Ck.
Дифференциальный атлас называется гладким, если он есть атлас класса C∞.
Два дифференциальных атласа одного класса называются совместными, если их объединение есть снова атлас того же класса.
Мы можем рассмотреть топологическое пространство с максимальным по включению дифференциальным атласом.
Дифференциальный атлас называется максимальным, если любой совместный с ним атлас является его подмножеством.
Базис топологического пространства - это такое семейство открытых в пространстве подмножеств, что любое открытое подмножество пространства представимо в виде объединения некоторого его подсемейства. Топологическое пространство удовлетворяет второй аксиоме счётности, если оно имеет счётный базис.
Дифференциальное многообразие размерности n класса k - это удовлетворяющее второй аксиоме счётности топологическое многообразие размерности n с зафиксированным на нём максимальным дифференциальным атласом класса Ck.
Гладкое дифференциальное многообразие - это дифференциальное многообразие с гладким атласом.
Шары разуй, тебя уже тыкали рылом в доказательство.
Двачую вопрос
Проще говоря, топологическое многообразие - это пространство, у которого вблизи каждой точки есть координаты.
Гладкое дифференциальное многообразие - это многообразие, у которого вблизи каждой точки возможен переход к другой системе координат, причём с использованием матана - якобиан, шмакобиан, вот это всё.
Загоните петуха обратно под шконку, он опять весь тред засрал.
Дай корректное определение натурального числа и он уйдёт. Я гарантирую это.
>У бурбаков, кстати, про эпсилон Гильберта ничего не сказано.
Тогда тебе стоит прочитать пикрелейтед, чтобы узнать основные философские концепты. Бурбаки считали их общеизвестными.
Плохая книжка, все на словах ни формальных систем нет, ни толкового изложения.
Как же ты заебал.
Ты имеешь ввиду не "корректное" а "устраивающее петуха"?
Потому что в данном контексте непустота пересечения этих множеств недоказана.
Пробелы сам расставишь
Уже сто раз написал. Докажем от противного. Допустим, аксиомы Пеано не определяют N. Тогда должно существовать как минимум одно натуральное число, не определяющееся этими аксиомами. Из того факта, что такого числа нет прямо следует, что все натуральные числа вписываются в Аксиомы Пеано, и стало быть, они однозначно определяют N.
Я тебя не ебал (в рот несчитается).
Ты противная дурашка, понимаешь что не можешь оперировать понятиями до их определения?
Ничуть не сторонник N-петуха, но обосрался в голос от твоей сверхманёвренности.
Со мной уже как минимум двое толковых математиков согласились в этом итт треде. Кроме того я приводил прямые цитаты Успенского и Степанова.
На самом деле унылые у него маневры, одну и ту же хуергу переписывает сто раз. Даже кнуёбок интереснее отвечал.
Еблан ты, аксиомы Пеано - это и есть определение, причем исчерпывающее. Как минимум до того момента пока ты не приведешь пример натурального числа, в них не вписывающегося. А до этого момента сасай-кудасай, придется тебе признать что я прав.
Почему ты не его сторонник? Ты считаешь аксиомы Пеано являются определением N и тебя не смущает тот факт, что без индукции они даже не формулируются???
Перед тем как требовать пример этого числа принеси мне построение аксиом Пеано без использования индукции на метаязыке иначе твой вопрос некорректен. Ты с тем же успехом можешь требоать посчитать 2 + 2 не дав определение что такое +.
>Ты считаешь аксиомы Пеано являются определением N
Да, считаю.
>тебя не смущает тот факт
Нет
>они даже не формулируются???
Иди нахуй.
> Да, считаю.
Это характерно для малолетнего долбоёба.
> Нет
Это характерно для малолетнего долбоёба.
> Иди нахуй.
Хуй тебе в рыло.
Самоутвердился? Теперь мамке похвастайся и иди уже нахуй.
>>
Я ебал твой мать.
Я ебал твой мать.
Знаешь, N-петух, идеологически я, может, с тобой и согласен, но мой опыт показывает, что все подобные многочасовые зануды являются как минимум психически нездоровыми, не говоря уже о самом факте засирания тредов.
Идеологически это как?
PS Вообще-то это твоё машинное обучение следует признать засиранием. N намного ближе к теоретической математике.
Утихомирься, или я пожалуюсь на тебя модератору.
кек, мамке своей пожалуйся
неловко, когда листки по которым ты учился теперь на двачах




















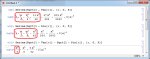


























1. Верно ли, что в каждом конечном графе имеются вершины одинаковой степени?
2. Верно ли, что если в конечной группе G выбрано подмножество A такое, что каждый g из G сопряжен некоторому a из A и элементы A попарно коммутируют, то G коммутативна?
3. Пусть A подмножество вещественной прямой. Верно ли, что не бывает такого, чтобы одновременно A имело нулевую меру и дополнение A было бы объединением счетного числа нигде не плотных?